Применение правила Лопиталя для вычисления пределов

Стр 1 из 17Следующая ⇒

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ

Государственное бюджетное профессиональное образовательное учреждение

города Москвы

«КОЛЛЕДЖ АВТОМОБИЛЬНОГО ТРАНСПОРТА № 9»

ГБПОУ КАТ № 9

УТВЕРЖДАЮ

Руководитель УП

__________ Прошева Н.Н.

«____»_______________2018г.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ДЛЯ ВЫПОЛНЕНИЯ ВНЕАУДИТОРНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

ПО ДИСЦИПЛИНЕ

ЕН.01 «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»

^{код и наименование дисциплины}

для специальности 09.02.04 «Информационные системы на автомобильном транспорте»

Разработал: преподаватель ГБПОУ КАТ №9 Жукова Т.С.

Рассмотрены и одобрены на заседании предметной (цикловой) комиссии

общеобразовательных дисциплин______________________________________________

наименование комиссии

от ____________________ протокол № _____

Председатель ПЦК ___________________________________ / Жукова Т.С.

2018

Пояснительная записка

Цель методических рекомендаций – оказать учащимся помощь при выполнении внеаудиторной самостоятельной работы и при подготовке к практическим работам, а также для отработки пропущенного материала. Рекомендации содержат описание всех предусмотренных программой тем:

Раздел 1. Элементы математического анализа и дифференциального и исчисления

Раздел 2. Элементы интегрального исчисления

Раздел 3. Дифференциальные уравнения

Раздел 4. Основы линейной алгебры

Раздел 5.Основы аналитической геометрии

Программа учебной дисциплины «Элементы высшей математики» направленна на формирование следующих знаний, умений:

умения:

· выполнять операции над матрицами и решать системы линейных уравнений,

· применять методы дифференцированного и интегрированного исчисления.

· решать дифференциальные уравнения

знания:

· основы математического анализа, линейной алгебры и аналитической геометрии,

· основы дифференцированного и интегрированного исчисления.

Критерии оценки

Основные требования к выполнению заданий состоят в том, чтобы:

– из представленного решения был понятен ход рассуждений обучающегося;

– ход решения был математически грамотным;

– представленный ответ был правильным.

Правильное выполнение заданий оценивается баллами. За правильное выполнение любого примера (задачи) обучающийся получает 1 балл.

Если приводится неверный ответ или ответ отсутствует, ставится 0 баллов. Баллы, полученные за все выполненные задания, суммируются.

Оценка результатов выполнения практической работы осуществляется согласно утвержденным критериям:

«Отлично» - 90% - 100% выполненных заданий.

«Хорошо» - 70% - 89% выполненных заданий.

«Удовлетворительно» - 50% - 69% выполненных заданий.

ВИДЫ ВНЕАУДИТОРНОЙ (САМОСТОЯТЕЛЬНОЙ) РАБОТЫ

По дисциплине ЕН.01 «Элементы высшей математики»

Специальности 09.02.04 «Информационные системы на автомобильном транспорте»

Наименование разделов, тем дисциплины	Виды внеаудиторной (самостоятельной) работы	Кол- во часов
Раздел 1. Элементы математического анализа и дифференциального и исчисления	Расчетная работа №1	8
	[3] Решение задач № 188-196, 205-206, 218-219	6
Раздел 2. Элементы интегрального исчисления	[3] Решение задач №254-255, 260-264, 276, 280-292	2
	Расчетная работа №2	7
	Подготовка опорного конспекта по теме «Интегрирование по частям»	2
Раздел 3. Дифференциальные уравнения	[3] Решение задач № 294-300	4
Раздел 3. Дифференциальные уравнения	Расчетная работа №3	5
Раздел 4. Основы линейной алгебры	Подготовка опорного конспекта по теме «Транспортная задача»	5
Раздел 4. Основы линейной алгебры	Расчетная работа №4	5
Раздел 5.Основы аналитической геометрии	[3] Решение задач № 331-334, 376-380, 389-391, 398-402	3
Раздел 5.Основы аналитической геометрии	Расчетная работа №5	4
Итого		51

РАЗДЕЛ 1. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА И ДИФФЕРЕНЦИАЛЬНОГО И ИСЧИСЛЕНИЯ

Вычисление пределов

Дифференцирование функций

Исследование функций

Задания для самостоятельной работы

Вычисление пределов

Сформулируем основные свойства пределов:

1. Предел постоянной равен самой постоянной.

2. Предел суммы конечного числа слагаемых равен сумме их пределов:

3. Предел произведения конечного числа множителей равен произведению их пределов:

В частности полезно запомнить, что , то есть постоянный множитель можно выносить за знак предела.

4. Предел частного равен частному пределов числителя и знаменателя, если предел знаменателя отличен от нуля:

Если функция определена и непрерывна в точке то предел функции в точке равен значению функции в этой точке, например

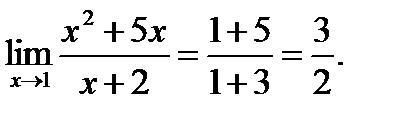Отметим, что все элементарные функции непрерывны в тех точках, где они определены. Поэтому для всех элементарных функций , если f(x) определена в точке x=a.

Отметим два важных факта, которые мы будем использовать при вычислении пределов.

Если ограниченная в окрестности точки x=a функция, а - бесконечно малая функция , то есть , то .

Если ограниченная в окрестности точки x=a функция, а - бесконечно большая функция, то есть , то .

Наибольшие трудности вызывает вычисление пределов функций в точках разрыва или на концах области определения. Если число не принадлежит области определения или или , то для нахождения предела необходимо специальное исследование. В этих случаях возможны следующие неопределенные ситуации, которые будем называть неопределенностями: (в случае вычисления предела частного),

Приведем ряд фактов, которые используются для раскрытия неопределенностей.

1. Первый замечательный предел:

Здесь имеет место неопределенность . Заметим, что на месте переменной под знаком предела может стоять любая функция при условии, что она является бесконечно малой при . То есть, верна более общая формула:

2. Второй замечательный предел:

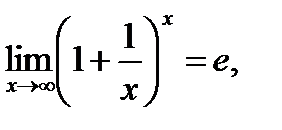или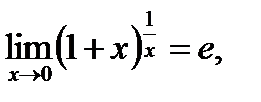

аналогично верны обобщенные формулы:

если

Существенно упрощает вычисление пределов использование эквивалентных функций.

Напомним, что функции и называются эквивалентными, если . Эквивалентность функций обозначается символом ~ .

Приведем некоторые часто используемые, эквивалентные в окрестности точки x=0 , функции.

Поскольку:

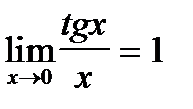Þ tg(x) ~x;

Þ arcsin(x) ~x;

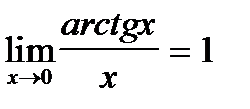Þ arctg(x) ~x;

Þ ~x;

Þ ~x.

Для эквивалентных функций верна следующая теорема о замене функций эквивалентными функциями:

1) предел отношения бесконечно малых функций равен пределу отношения эквивалентных им функций,

2) предел произведения бесконечно малых функций равен пределу произведения эквивалентных им функций

Например,

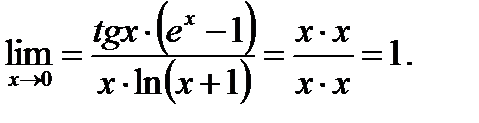
Примеры

Задача. Найти предел .

Преобразуем это выражение. В каждом из многочленов вынесем множитель х в старшей степени за скобки. Получим:

= =

= = = = .

Ответ: .

В процессе вычисления предела мы воспользовались теоремами о пределе суммы, произведения, частного, а так же теоремой о делении ограниченной функции на бесконечно большую.

К примеру .

Задача. Найти предел

Решение.

Здесь возникает неопределенность вида . Для нахождения этого предела вынесем из-под знаков радикалов и за скобки наивысшие степени , в результате получим:

Ответ:

В следующей задаче применяется умножение и деление на сопряженное выражение. Суть этого приема заключена следующих формулах:

;

Задача. Найти предел .

Данный предел является пределом вида ¥-¥. Умножим и разделим выражение под знаком предела на выражение сопряженное этой сумме . Получим

= =

= =(далее ход решения аналогичен тому, который был использован в предыдущей задаче)= = =(заметим, что при х<0 имеем )= = = .

Ответ:-2.

Задача . Найти .

Значение x=-1 является корнем каждого из многочленов, стоящего в числителе и знаменателе дроби. Аналогичным образом разложив на множители, получаем:

= = =6.

Ответ: 6.

Решение следующей задачи связано с использованием первого замечательного предела . При решении подобных задач полезно использовать два соотношения.

Первое. . Для его вывода сделаем замену переменных 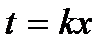. Тогда , .Тогда получаем

Второе. . Это соотношение получается следующим путем .

Задача. Найти .

Преобразуем данное выражение = =

= = (воспользуемся теоремой о пределе произведения, а также формулой )=

= . Ответ: .

Задача 6. Найти .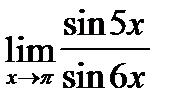

Сделаем замену переменной t=x-p. Тогда t®0 при x®0. Следовательно: x=t+p, sin5x=sin(5t+5p)=-sin5t, sin6x=sin(6t+6p)=sin6t. Получаем = .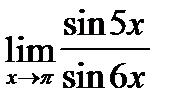

Ответ: .

Решение следующей задачи требует знания второго замечательного предела: . Укажем еще на один факт, который следует из второго замечательного предела и бывает полезен при решении подобных задач: .

Чтобы получить такой вывод, сделаем замену переменных x=kt. Тогда t®¥ при t®¥. Получаем:

Например .

Задача. Найти предел:

Решение.

Здесь неопределенность вида . Сведем этот предел ко второму замечательному пределу. В основании степени, стоящей под знаком предела, выделим единицу (разделив с остатком числитель на знаменатель):

Далее преобразуем выражение под знаком предела, выделив второй замечательный предел:

= .

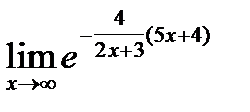В конце решения примера сделан переход к пределу под знаком показательной функции.

Ответ:

В следующей задаче использована замена функций на эквивалентные.

Задача. Найти .

Воспользуемся эквивалентными функциями при .

Так как : , а sinx~x, то ~2 ~ .

Аналогично ~ , sin5x~5x. Получаем = .

Ответ: .

Задача. Найти предел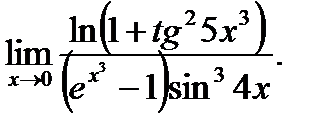

Решение.

Так как

при

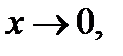
то

Ответ:

Задача. Найти .

Сделаем замену переменной . Тогда . Следовательно при . Получаем

= =3.

Ответ: 3.

Задача. Найти предел

Решение.

Здесь неопределенность Преобразуем знаменатель дроби по формуле разности косинусов:

Для нахождения полученного предела применим теорему о замене функций эквивалентными функциями.

Поскольку, при

То

Ответ:

Дифференцирование функции

Операция нахождения производной называется дифференцированием функции. Производная функции y=у(x) обозначается либо , либо .

Сформулируем основные правила дифференцирования:

1. Производная постоянной:

2. Производная произведения:

3. Постоянный множитель можно вынести за знак производной: .

4. Производная частного:

5. Теорема о производной сложной функции. Пусть где , тогда

Приведем формулы производных основных элементарных функций:

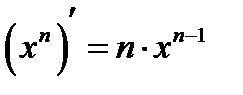Полезно запомнить частный случай этой формулы

Задача.

Найти производную , если .

Используя формулу производной произведения, получаем

Далее воспользуемся правилом дифференцирования сложной функции. Получаем

Ответ: .

Применение правила Лопиталя для вычисления пределов

Сформулируем правило Лопиталя:

Предел отношения двух бесконечно малых или бесконечно больших величин равен пределу отношения их производных (если последний предел существует):

Правило Лопиталя можно применять только в случае наличия неопределенности или . Для того, чтобы использовать правило Лопиталя в других неопределенностях, необходимо предварительно эти неопределенности преобразовать к неопределенности или .

Рассмотрим примеры.

Рассмотренный пример иллюстрирует тот факт, что правило Лопиталя допустимо применять несколько раз, если отношение производных также представляет собой неопределенность вида или .

2. .

Приведенные выше пределы могут быть вычислены не только по правилу Лопиталя, но и путем элементарных преобразований. Рассмотрим примеры, решение которых существенно упрощается с использованием правила Лопиталя.

3. .

4. .

Исследование функции

Напомним определение локального максимума и минимума функции.

Точка называется точкой локального максимума (минимума) функции , если существует такая окрестность точки , что для всех точек , принадлежащих этой окрестности, выполняется неравенство ( ).

Точки локального максимума и локального минимума называются точками экстремума функции.

Сформулируем теорему о необходимом условии существование экстремума.

Теорема Ферма (необходимое условие существования экстремума)

Точками экстремума непрерывной функции могут быть только такие точки, в которых производная этой функции или равна нулю или не существует.

Точки, в которых функция обращается в ноль или терпит разрыв, будем называть критическими точками этой функции.

Если на некотором интервале функция имеет единственную точку экстремума и эта точка является точкой максимума (минимума), то значение функции в этой точке будет наибольшим (наименьшим) на всем интервале.

Сформулируем достаточные условия экстремума функции:

Если при переходе через критическую точку производная функции меняет знак с плюса на минус (с минуса на плюс), то эта точка является точкой максимума (минимума) функции. (Предполагается, что функция определена и непрерывна в окрестности данной точки.)

Дата добавления: 2019-09-13; просмотров: 600; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!