Системы линейных алгебраических уравнений
Опр. Система к линейных уравнений с n неизвестными:
а11 х1 + а12 х2 + … + а1n xn = b1
a21 x1 + a22 x2 + ... + a2n xn = b2
. . . . . .
ak1 x1 + ak2 x2 + ... + akn xn = bk, где аij – коэффициенты системы, bi – свободные члены, хj – неизвестные.
Матричная запись системы.
Рассмотрим матрицы:
a11 … а1n
А = . . . . . – матрица коэффициентов (её называют матрицей системы),
ak1 ... akn
b1
В = .. – столбец свободных членов,
bk
х1
Х = .. – столбец неизвестных.
хn
Система теперь может быть записана в виде матричного уравнения:
АХ = В.
Решение системы n линейных уравнений с n неизвестными с помощью обратной матрицы в случае, когда матрица системы невырождена.
В этом случае система имеет единственное решение
х1
.. = X = 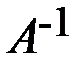 B .
B .
хn
Доказательство: 1) Х = 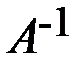 В удовлетворяет матричному уравнению АХ = В. Действительно, подставим это значение Х в уравнение:
В удовлетворяет матричному уравнению АХ = В. Действительно, подставим это значение Х в уравнение:
А( 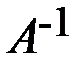 B) = B,
B) = B,
(A 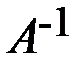 )B = B,
)B = B,
I B = B,
B = B – верно
2) Предположим, что Х – любое решение матричного уравнения АХ = В.
Умножим слева это равенство на 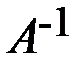 .
.
Получим 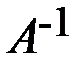 (AX) =
(AX) = 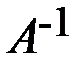 B,
B,
( 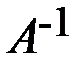 A)X =
A)X = 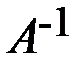 B,
B,
I X = 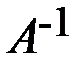 B,
B,
X = 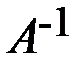 B.
B.
Таким образом всякое решение матричного уравнения совпадает с решением Х = 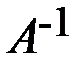 B. Тем самым доказана единственность решения.
B. Тем самым доказана единственность решения.
|
|
|
Пример: Решим систему
2х – 3y = -7
3x + 5y = -1
2 -3 -7 х
A = 3 5 ; В = -1 ; Х = y
1 5 3
 19 -3 2
19 -3 2
x 1 5 3 -7 1 -38 -2
y = Х = 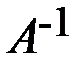 B = 19 -3 2 -1 = 19 19 = 1
B = 19 -3 2 -1 = 19 19 = 1
х = - 2
Ответ: y = 1 - единственное решение системы.
Рассмотренный метод трудоёмок в случаях, когда уравнений (и неизвестных) больше 2-х. Метод не работает, если число уравнений не равно числу неизвестных, или когда матрица системы хотя и квадратна, но вырождена (тогда не существует 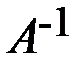 ). Тем не менее, рассмотренный случай (число неизвестных = числу уравнений) является наиболее часто встречающимся, а запись единственного решения системы в виде Х =
). Тем не менее, рассмотренный случай (число неизвестных = числу уравнений) является наиболее часто встречающимся, а запись единственного решения системы в виде Х = 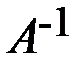 B является теоретически очень выразительной.
B является теоретически очень выразительной.
Выполнив умножение 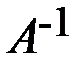 B, и записав результат с помощью определителей, получим метод Крамера.
B, и записав результат с помощью определителей, получим метод Крамера.
Метод Крамера решения системы n линейных уравнений с n неизвестными в случае, когда матрица системы невырождена.
Рассмотрим систему:
а11 х1 + а12 х2 + … + а1n xn = b1
a21 x1 + a22 x2 + ... + a2n xn = b2
. . . . . . . .
an1 x1 + an2 x2 + ... + ann xn = bn
Обозначим
a11 ... a1n
= … - определитель матрицы системы,
|
|
|
an1 ... ann
b1 a12 ... a1n
x1 = … - определитель, полученный из определителя
bn an2 ... ann
подменой 1-го столбца на столбец свободных членов
а11 b1 ... a1n
x2 = … - определитель, полученный из определителя подменой
an1 bn ... ann
2-го столбца на столбец свободных членов
. . . . . . . .
a11 ... a1,n-1 b1
хn = - определитель, полученный из определителя подменой
a1n ... an,n-1 bn
n-го столбца на столбец свободных членов
Если = 0 система имеет единственное решение
х1 = х1/
x2 = x2/
. . . . . . .
xn = xn/
Пример: Решим систему
2х – 3y = -7
3x + 5y = -1
2 -3
= 3 5 = 19
-7 -3
x = -1 5 = -38
2 -7
y = 3 -1 = 19
x = x/ = - 38/19 = - 2
y = y/ = 19/19 = 1
х = - 2
Ответ: y = 1 - единственное решение системы.
Метод Крамера с вычислительной точки зрения чуть удобнее, чем метод обратной матрицы, тем, что даёт раздельные формулы для каждой неизвестной. Но по содержанию метод Крамера тождественен методу обратной матрицы.
Оба метода хороши тем, что дают ответ в виде законченных формул.
Следующий метод Гаусса не обладает этим достоинством, но зато является универсальным, применимым к любой системе линейных уравнений, точным методом.
|
|
|
Метод последовательного исключения неизвестных (метод Гаусса) решения систем линейных уравнений.
Элементарными преобразованиями системы линейных уравнений называют следующие три типа преобразований:
1) Перемена местами любых 2-х уравнений системы.
2) Умножение (или деление) любого уравнения системы на ненулевое число.
3) Замена одного из уравнений системы на его сумму с другим уравнением.
Легко доказывается, что элементарные преобразования приводят к системе равносильной исходной (т.е. имеющих то же множество решений).
Сначала рассмотрим метод Гаусса на примере:
Пример: Решим систему
х – 2y + z = 0 (- 2) (- 3)
2x +y – 2z = - 2 +
3x + y + z = 8 +
Прибавим ко 2-му уравнению 1-е уравнение, умноженное на (- 2), а к 3-му уравнению 1-е уравнение, умноженное на (- 3). Получим систему равносильную исходной:
x – 2y + z = 0
5y – 4z = -2 (- 7)
7y – 2z = 8 5 +
Тем самым неизвестное х исключается из 2-го и 3-го уравнения.
Исключим теперь переменную y из 3-го уравнения, используя 2-е уравнение. Для этого заменим 3-е уравнение на сумму 2-го уравнения, умноженного на (- 7) и 3-го уравнения, умноженного на 5. Получим систему:
|
|
|
х - 2y + z = 0
5y – 4z = -2
18z = 74
Теперь мы можем найти z из последнего уравнения, затем найти y из 2-го уравнения (т.к. мы уже знаем z), и, наконец, найти х из 1-го уравнения (мы уже знаем y и z). Итак
х = 2y – z = 4 – 3 = 1
y = 1/5 (4z – 2) = 1/5 (12 – 2) = 2
z = 3
Вычисления осуществляются снизу вверх, что мы отметили стрелочкой.
Можно было бы производить элементарные преобразования системы и дальше, только теперь уже снизу вверх: исключая z из 1 и 2-го уравнения, затем исключая y из 1-го уравнения:
х – 2y + z = 0 x – 2y + z = 0 x – 2y = -3 5
5y – 4z = -2 ó 5y – 4z = -2 + ó 5y = 10 2 +
18z = 74 : 18 z = 3 4 (- 1) + z = 3
5x = 5 : 5 x = 1
ó 5y = 10 : 5 ó y = 2
z = 3 z = 3
Разберем еще один пример.
Пример: 2х + y – z = 0 x + 2y + z = 3 (- 2) (- 1)
x + 2y + z = 3 ó 2x + y – z = 0 + ó
x – y – 2z = -3 x – y – 2z = -3 +
x + 2y + z = 3 x + 2y + z = 3 x + 2y + z = 3
- 3y – 3z = -6 : (- 3) ó y + z = 2 (- 1) ó y + z = 2
- 3y – 3z = -6 : (- 3) y + z = 2 + 0 = 0
Последнее уравнение системы не вносит никаких ограничений для значений неизвестных, поэтому может быть исключено из системы:
x + 2y + z = 3
ó y + z = 2
Неизвестной z можно придавать любые значения. Такие неизвестные называются «свободными». Остальные переменные х и y выражаются через z.
x = 3 – 2y – z = 3 – 2(2 – z) – z = - 1
y = 2 – z
z = z - любое
Рассматриваемая система имеет бесконечное множество решений:
x = -1 – 4с
y = 2 – c
z = c, где с – любое число
Последнюю систему невозможно было бы решить методом Крамера или с помощью обратной матрицы. Матрица этой системы, как легко проверить, вырождена.
Дата добавления: 2019-09-13; просмотров: 180; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
