Некоторые свойства неопределенного интеграла.
1. Согласно определению неопределенного интеграла его производная равна подынтегральной функции, то есть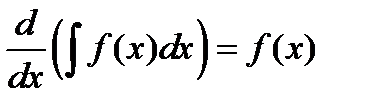 
.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению: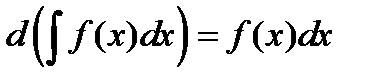 
.
3.Неопределенный интеграл от производной некоторой функции равен этой функции плюс произвольная постоянная: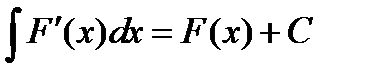 
.
4. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная: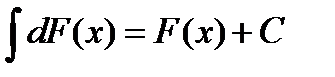 
.
Следующие свойства интегралов вытекает из соответствующих свойств производных.
5. Неопределенный интеграл от суммы (или разности) двух функций равен сумме (или, соответственно, разности) неопределенных интегралов от этих функций: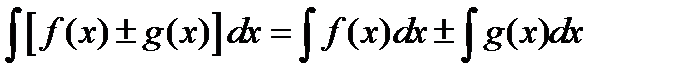 
.
6.Постоянный множитель можно выносить за знак неопределенного интеграла: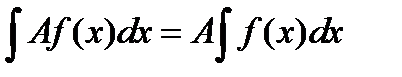 
.
7. Из формулы производной произведения вытекает
Формула интегрирования по частям:
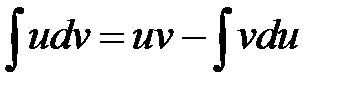
8.Из формулы производной сложной функции вытекает формула:
( Замена переменной в неопределенном интеграле )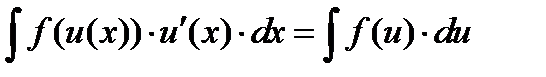 
Эту формулу используют как слева направо, так и справа налево.
1)справа налево:
Например, пусть требуется вычислить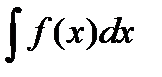 
и по каким-то причинам нам удобно сделать замену переменной в виде 
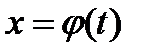, где 
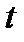- новая независимая переменная. Тогда 
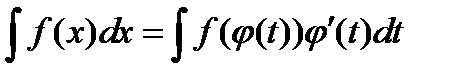. При этом, конечно, предполагаем, что после вычисления интеграла в правой части мы подставим вместо 
, выражение через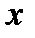 
из соотношения 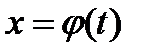(функция 
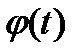должна быть обратима).
2)слева направо:
Например, пусть нам известно, что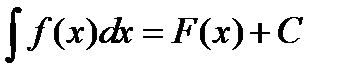 
. Требуется вычислить интеграл вида 
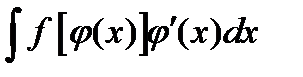. Тогда 
.
|
|
|
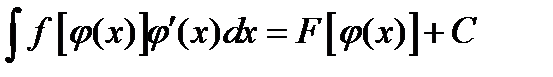Рассмотрим примеры.
Использование замены переменной
Задача. Найти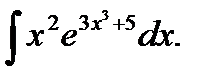 
Решение:
Обозначим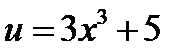 
. Тогда для дифференциала данной функции имеем выражение 
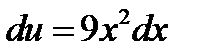. Следовательно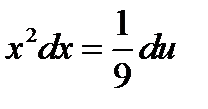 
Подставляя в исходное выражение, получаем
.
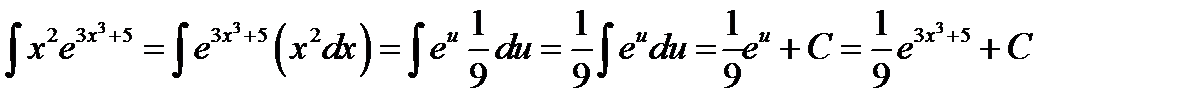Иногда не вводят обозначение для новой переменной, а все выражение для новой переменной через старую используют как ее имя, записывая это выражение под знаком дифференциала. Это и называют «подведением под знак дифференциала». В рассмотренном примере: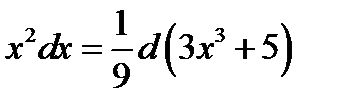 
, мы можем записать 
.
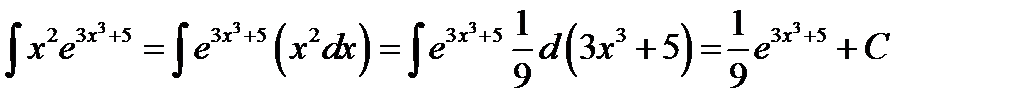Задача. Найти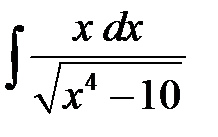 
.
Решение:
Обозначим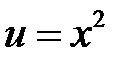 
. Тогда 
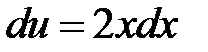. Следовательно, 
.
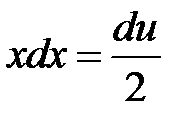Получаем
.
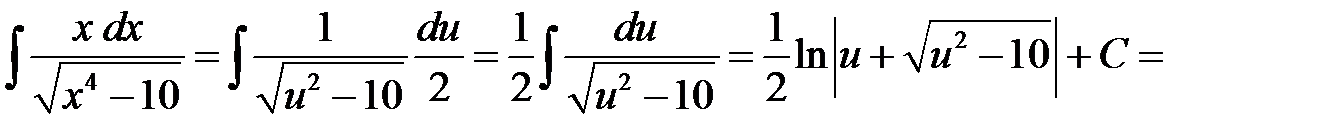
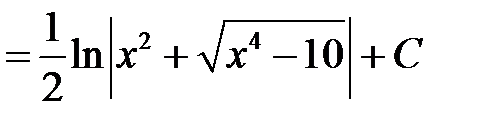Задача. Найти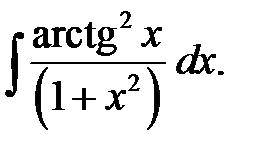 
Решение:
Обозначим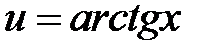 
. Тогда 
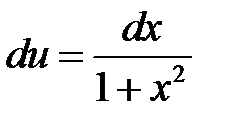. Следовательно, 
.
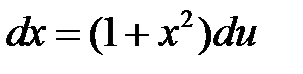Получаем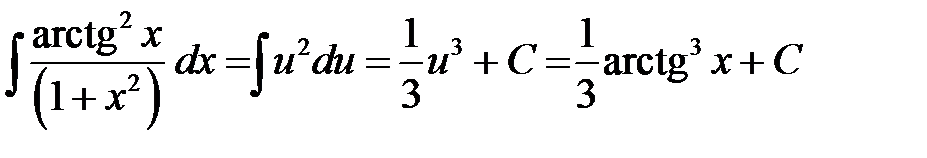 
.
Применение формулы интегрирования по частям для вычисления неопределенных интегралов.
Формула интегрирования по частям имеет вид
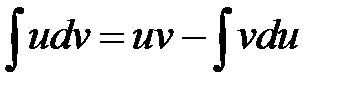
В этой формуле за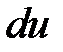 
и 
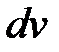обозначены дифференциалы некоторых функций.
На всякий случай еще раз напомним определение дифференциала функции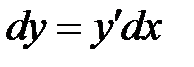 
, а так же формулу восстановления функции по ее дифференциалу 
.
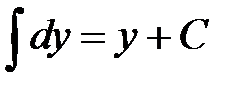Задача. Найти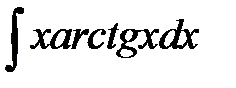 
.
При использовании формулы интегрирования по частям важно правильно на первом этапе разбить подынтегральное выражение на два множителя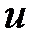 
и 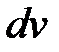. Неудачное разбиение может привести не к упрощению, а, наоборот, к усложнению примера. В указанном примере обозначим 
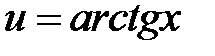. Всю оставшуюся часть подынтегрального выражения мы обозначим 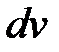, то есть 
.
|
|
|
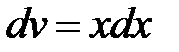Тогда имеем:
;
.
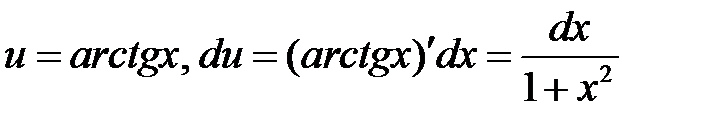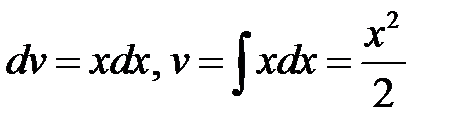Применяя формулу интегрирования по частям, получаем
.
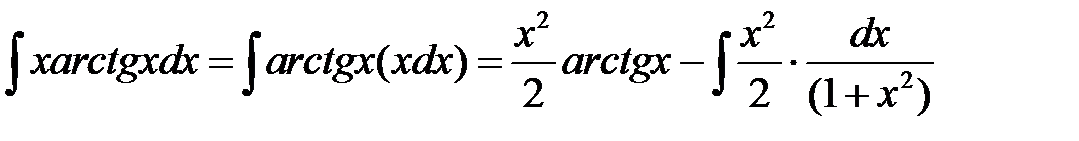Для вычисления последнего интеграла подынтегральное выражение преобразуем к виду
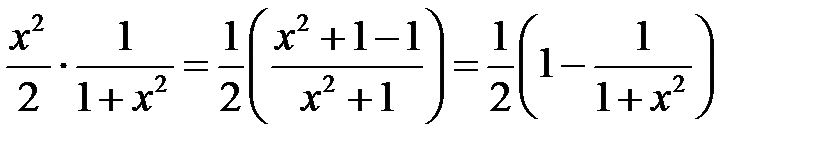
Тогда получаем
.
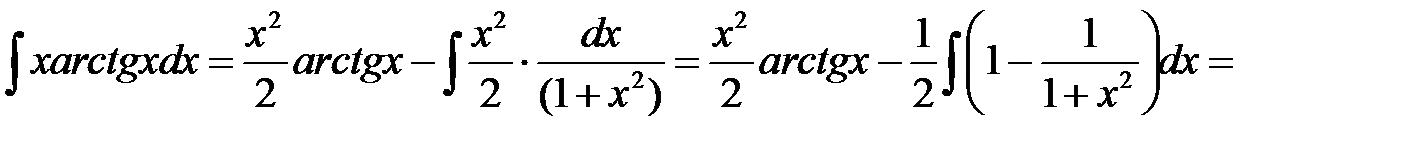
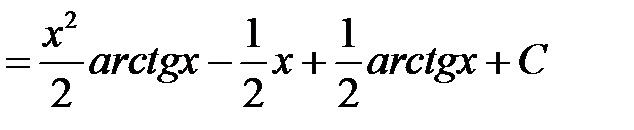Ответ: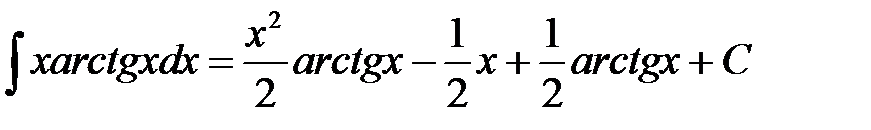 
.
Определенный интеграл
Определение. Если существует предел интегральных сумм при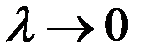 
, и этот предел не зависит ни от способа разбиения, ни от способа выбора точек 
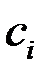, то функция 
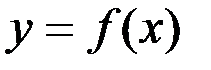называется интегрируемой на отрезке 
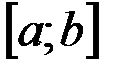, а значение предела называется определенным интегралом от данной функции по отрезку 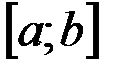, и обозначается 
.
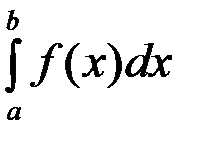«Всякая функция, непрерывная на отрезке, является интегрируемой по этому отрезку».
Свойства определенного интеграла.
При формулировке свойств мы будем предполагать, что речь идет о функциях, интегрируемых по отрезку.
1. 
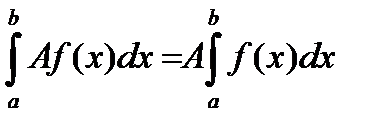, где А – постоянная величина.
2. 
.
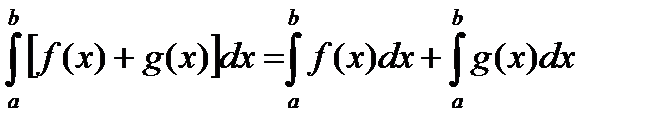3. 
.
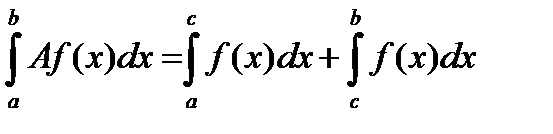Кроме того, по определению полагают
.
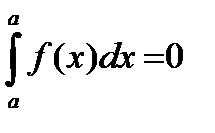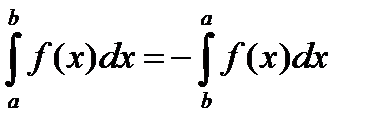при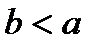 
.
Дата добавления: 2019-09-13; просмотров: 199; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!