Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору
Пусть прямая проходит через точку  перпендикулярно вектору
перпендикулярно вектору 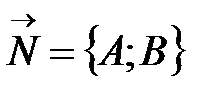 .
.

Точка  лежит на прямой тогда и только тогда, когда векторы
лежит на прямой тогда и только тогда, когда векторы 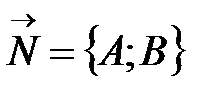 и
и  перпендикулярны. Векторы
перпендикулярны. Векторы  и
и  перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, то есть
перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, то есть  . Используя формулу вычисления скалярного произведения векторов, заданных своими координатами, уравнение искомой прямой записываем в виде
. Используя формулу вычисления скалярного произведения векторов, заданных своими координатами, уравнение искомой прямой записываем в виде
 (2)
(2)
Пример. Найти уравнение прямой, проходящей через середину отрезка АВ перпендикулярно этому отрезку если координаты точек соответственно равны А(1;6), В(5;4).
Будем рассуждать следующим образом. Чтобы найти уравнение прямой мы должны знать точку, через которую эта прямая проходит, и вектор перпендикулярный этой прямой. Вектором, перпендикулярным данной прямой, будет вектор  , поскольку, по условию задачи, прямая перпендикулярна отрезку АВ. Точку
, поскольку, по условию задачи, прямая перпендикулярна отрезку АВ. Точку  определим из условия, что прямая проходит через середину АВ. Имеем
определим из условия, что прямая проходит через середину АВ. Имеем  . Таким образом
. Таким образом  и уравнение примет вид
и уравнение примет вид  .
.
Выясним вопрос, проходит ли эта прямая через точку М(7;3).
Имеем  , значит, эта прямая не проходит через указанную точку.
, значит, эта прямая не проходит через указанную точку.
Уравнение прямой, проходящей через данную точку, параллельно данному вектору
Пусть прямая проходит через точку  параллельно вектору
параллельно вектору 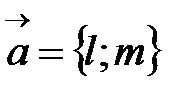 .
.

Точка  лежит на прямой тогда и только тогда, когда векторы
лежит на прямой тогда и только тогда, когда векторы 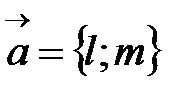 и
и  колинеарны. Векторы
колинеарны. Векторы 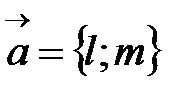 и
и  колинеарны тогда и только тогда, когда их координаты пропорциональны, то есть
колинеарны тогда и только тогда, когда их координаты пропорциональны, то есть
|
|
|
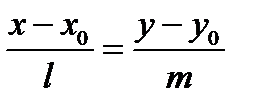 (3)
(3)
Полученное уравнение и является уравнением искомой прямой.
Уравнение (3) представим в виде
 , где
, где  принимает любые значения
принимает любые значения  .
.
Следовательно, можем записать
 , где
, где  (4)
(4)
Система уравнений (4) называется параметрическими уравнениями прямой.
Рассмотрим пример. Найти уравнение прямой, проходящей через точки  . Мы можем построить уравнение прямой, если знаем точку и параллельный или перпендикулярный ей вектор. Точек в наличии целых две. Но если две точки лежат на прямой, то вектор, их соединяющий будет параллелен этой прямой. Поэтому воспользуемся уравнением (3), взяв в качестве вектора
. Мы можем построить уравнение прямой, если знаем точку и параллельный или перпендикулярный ей вектор. Точек в наличии целых две. Но если две точки лежат на прямой, то вектор, их соединяющий будет параллелен этой прямой. Поэтому воспользуемся уравнением (3), взяв в качестве вектора 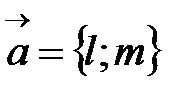 вектор
вектор  . Получаем
. Получаем
 (5)
(5)
Уравнение (5) называется уравнением прямой, проходящей через две данные точки.
Общее уравнение прямой
Определение. Общим уравнением линии первого порядка на плоскости называется уравнение вида  , где
, где  .
.
Уравнение вида  называется общим уравнением прямой на плоскости.
называется общим уравнением прямой на плоскости.
|
|
|
Формула вычисления расстояния от произвольной точки плоскости до прямой, заданной общим уравнением.
Пусть имеется прямая  и точка
и точка  . Требуется определить расстояние от указанной точки до прямой.
. Требуется определить расстояние от указанной точки до прямой.
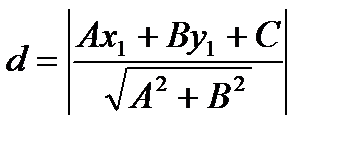 .
.
Пусть даны две прямые, заданные общими уравнениями
 ,
,  . Тогда векторы
. Тогда векторы 
 перпендикулярны первой и второй прямой соответственно. Угол
перпендикулярны первой и второй прямой соответственно. Угол  между прямыми равен углу между векторами
между прямыми равен углу между векторами  ,
,  .
.
Формула для определения угла между прямыми имеет вид:
 .
.
Условие перпендикулярности прямых имеет вид:
 .
.
Прямые параллельны или совпадают тогда и только тогда, когда векторы 
 колинеарны. При этом условие совпадения прямых имеет вид:
колинеарны. При этом условие совпадения прямых имеет вид:  ,
,
а условие отсутствия пересечения записывается в виде: 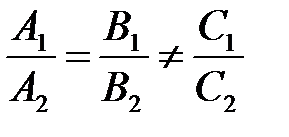 .
.
У равнение 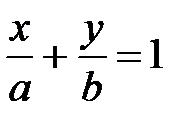 называется уравнением прямой в отрезках.
называется уравнением прямой в отрезках.

Угловым коэффициентом прямой  называется тангенс угла наклона этой прямой к оси
называется тангенс угла наклона этой прямой к оси 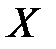 . Пусть прямая отсекает на оси
. Пусть прямая отсекает на оси  отрезок
отрезок  и имеет угловой коэффициент
и имеет угловой коэффициент  . Пусть точка
. Пусть точка  лежит на данной
лежит на данной
прямой.

Тогда  =
=  =
=  . И уравнение прямой запишется в виде
. И уравнение прямой запишется в виде  .
.
Пусть прямая проходит через точку  и имеет угловой коэффициент
и имеет угловой коэффициент  . Пусть точка
. Пусть точка  лежит на этой прямой.
лежит на этой прямой.

Тогда  =
=  .
.
Дата добавления: 2019-09-13; просмотров: 573; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
