Вычисление площадей плоских фигур с помощью определённого интеграла.
Основная формула для вычисления площади плоских фигур с помощью определенного интеграла
Рассмотрим постановку задачи о площади криволинейной трапеции.
Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).
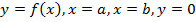 .
.
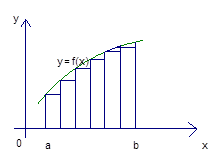
Рис. 1. Площадь криволинейной трапеции
Как мы пытались ее решить:
Первый способ.
Разбили отрезок 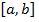 на
на 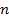 одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили
одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили 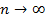 в пределе
в пределе 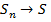 и
и
получили искомую площадь S. Ввели обозначение 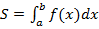 .
.
Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.
Затем мы получили точное решение задачи следующим образом: рис. 2:
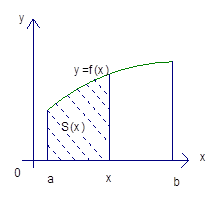
Рис. 2. Функция S (x)
Ввели функцию 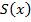 . Каждому
. Каждому  площадь под соответствующей частью кривой
площадь под соответствующей частью кривой 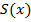 . Так, введенная функция удовлетворяет единственному закону, а именно:
. Так, введенная функция удовлетворяет единственному закону, а именно:
Каждому 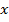 соответствует единственное значение
соответствует единственное значение 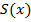 .
.
Мы доказали, что производная этой же функции 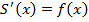 и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции
и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции 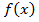 и взять приращение этих первообразных. То есть взять первообразную в точке
и взять приращение этих первообразных. То есть взять первообразную в точке 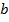 и отнять первообразную в точке
и отнять первообразную в точке 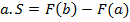 . И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
. И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
|
|
|
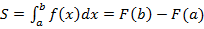 .
.
Методика нахождения площади на примере
Методику нахождения площади рассмотрим сначала на относительно простом примере.
Пример 1.
Найти площадь фигуры, ограниченной линиями 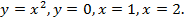
Решение.
Вот искомая площадь:
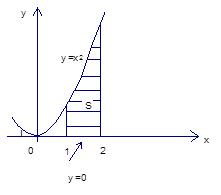
Рис. 3. Площадь
Вот формула:
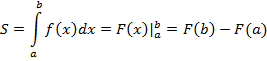
Это общая формула. Конкретно к нашему случаю она применима так:
Пределы интегрирования 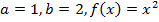 .
.
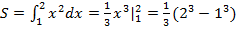 =
=  .
.
Вычислили площадь криволинейной фигуры.
Ответ: 
В следующей задаче площадь искомой фигуры образовывается с помощью 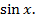 А именно:
А именно:
Пример 2
Найти площадь фигуры, ограниченной линиями 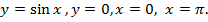
Решение.
Посмотрим, как выглядит фигура (рис. 4).
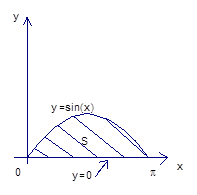
Рис. 4. Фигура, ограниченная линиями 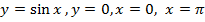
Формула та же самая: 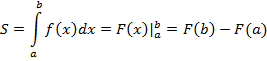
В нашем случае 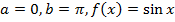 . Итак, надо найти определенный интеграл
. Итак, надо найти определенный интеграл
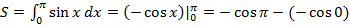 =-(-1)+1=1+1=2.
=-(-1)+1=1+1=2.
Искомая площадь найдена, и ответ получен.
Ответ: 2
Пример 3
Найти площадь фигуры, ограниченной линиями 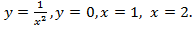
Решение.
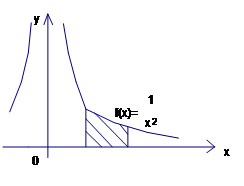
Рис. 5. Площадь фигуры, ограниченной линиями 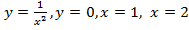
Формула для площади та же самая:
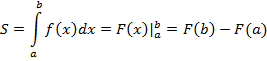
В нашем случае
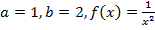 .
.
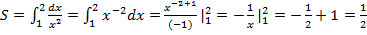 .
.
Ответ: 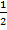
В следующем примере ищется площадь под параболой.
Пример 4
Найти площадь фигуры, ограниченной линиями 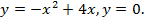
Решение.
Схематически изобразим параболу
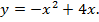
Корни 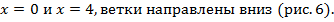
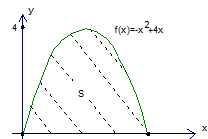
Рис. 6. Парабола 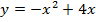
Применим известную формулу 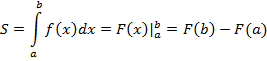
И применим ее для данной функции 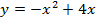 и пределов интегрирования
и пределов интегрирования
|
|
|
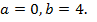
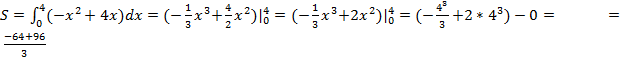
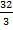 .
.
Искомая площадь найдена. 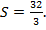
Ответ: 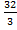
Пример 5
Найти площадь фигуры, ограниченной линиями : у=х2 + 2, у=0, х= -2, х=1.
Решение.
Схематически изобразим параболу. Выполним чертеж (обратите внимание, что уравнение у=0 задает ось Ох).
В этом заключается геометрический смысл определённого интеграла.
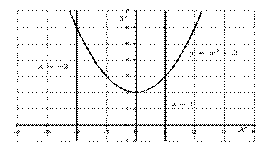
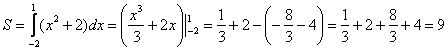
Ответ: S = 9 ед2
Дата добавления: 2019-09-13; просмотров: 215; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
