РАЗДЕЛ 1. Математический анализ.
Тема 1.1 Дифференциальное исчисление
В условии задач этой части задания на производную, в отличие от рассмотренных ранее, отсутствуют рисунки и графики. Для их решения необходимо применять аналитический подход, т.е. уметь вычислять производные функций, знать уравнение касательной к графику функции и т.п.
Процесс вычисления производных называют дифференцированием. Перед решением следующих задач стоит повторить формулы и правила дифференцирования функций.
Формулы дифференцирования функций

Правила дифференцирования функций
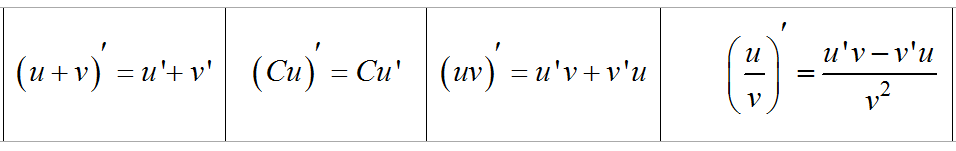
Правила можно сформулировать и словами.
1. Производная суммы равна сумме производных.
2. Постоянный множитель можно выносить за знак производной.
3. Производная произведения равна "производная первого сомножителя, умноженная на второй, плюс производная второго сомножителя, умноженная на первый".
4. Производная дроби равна "производная числителя, умноженная на знаменатель, минус производная знаменателя, умноженная на числитель, и деленные на знаменатель в квадрате".
Пример вычисления производной.
Вычислить производную функции f(x) = −x4 + 6x3 + 5x + 23.
f '(x) = (−x4 + 6x3 + 5x + 23)';
По правилу (1) дифференцирования суммы:
(−x4 + 6x3 + 5x + 23)' = (−x4)' + (6x3)' + (5x)' + (23)'.
По правилу 2 выносим за скобки числовые коэффициенты:
(−x4)' + (6x3)' + (5x)' + (23)' = −(x4)' + 6(x3)' + 5(x)' + (23)';
Переходим к формулам дифференцирования.
По формуле (xn)' = nxn − 1:
(x4)'= 4x4 − 1 = 4x3;
(x3)'= 3x3 − 1 = 3x2.
Для третьего слагаемого используем формулу (x)'= 1, а для последнего слагаемого формулу (с)' = 0 (производная константы равна нулю),
|
|
|
т.е. (23)' = 0.
Получим: −(x4)' + 6(x3)' + 5(x)' + (23)' = −4x3 + 6·3x2 + 5·1 + 0 =
= −4x3 + 18x2 + 5.
Следовательно: f '(x) = −4x3 + 18x2 + 5.
Задачи на физический смысл производной.
Физический смысл производной заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y = f(x).
Это может означать, например, следующее:
Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
Если же мы рассматриваем в качестве функции мгновенную скорость автомобиля, то производная задает изменение его ускорения.
Если мы рассматриваем функцию, задающую зависимость объема произведенной продукции от времени, то производная позволит узнать, как изменялась со временем производительность труда на этом предприятии.
Если мы рассматриваем электромагнитные волны, то нам могут потребоваться функции, характеризующие изменение со временем электрического и магнитного полей, а также их производные - скорости изменения этих полей, ведь величина магнитного поля пропорциональна скорости изменения электрического поля.
И т.п.
|
|
|
Решая конкретные текстовые задачи на скорость процесса с применением производной, следует не забывать о размерностях величин. Если переменная y, заданная функцией f(x) измеряется в некоторых единицах [y], а её аргумент в единицах [x], то производная (скорость) измеряется в единицах [y/x].
Пример1:
Точка движется по закону s(t)=2t³-3t (s – путь в метрах, t – время в секундах). Вычислите скорость движения точки, ее ускорение в момент времени 2с
| Дано: | Решение: |
| s(t)= 2t³-3t t=2с ______________ υ(2)=? а(2)=? | υ(t)=s’(t) υ(t)= (2t³-3t)’=6t²-3 υ(2)= 6·2²-3=21 м/с a(t)=υ’(t) а(t)=(6t²-3)’=12t a(2)=12·2=24м/с² Ответ: υ(2)= 21 м/с; a(2)= 24м/с² |
Пример 2:
Маховик вращается вокруг оси по закону φ(t)= t4-5t. Найдите его угловую скорость ω в момент времени 2с (φ – угол вращения в радианах, ω – угловая скорость рад/с)
| Дано: | Решение: |
| φ(t)=t4-5t t=2с ______________ φ(2)=? | ω(t)= φ’(t) ω(t)=(t4-5t)’= 4t³-5 ω(2)=4·2³-5=32-5=27рад/c Ответ: ω(2)= 27рад/c |
Дата добавления: 2019-09-13; просмотров: 172; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
