Закон сохранения момента импульса

Для систем материальных точек и при движении твёрдого тела выполняется уравнение моментов:

Скорость изменения момента импульса системы материальных точек равна сумме моментов внешних сил, действующих на все частицы этой системы.

Опираясь на него, мы можем сформулировать ещё один закон сохранения: Если сумма моментов всех внешних сил, действующих на тела системы равна нулю, то момент импульса системы не меняется с течением времени (т.е. сохраняется).

Если равна нулю сумма проекций моментов внешних сил на некоторое направление, например, закреплённую ось вращения Z, то сохраняется проекция момента импульса системы только на это направление:

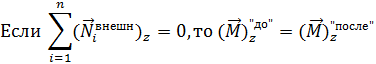
В частности, для систем с переменным моментом инерции выполняется равенство:

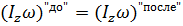
17. Работа силы. Механическая энергия – кинетическая и потенциальная. Связь силы и потенциальной энергии.

(Опр.) Элементарной работой δ A называется произведение проекции силы на направление малого перемещения точки приложения силы dl̄ на модуль этого перемещения: 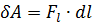или

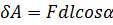
(Опр.) Работа на конечном участке траектории вычисляется как сумма элементарных работ:

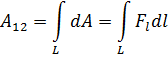
Работа силы – величина скалярная и зависит от взаимной ориентации векторов силы и скорости.

Работа при вращении тела относительно закреплённой оси:

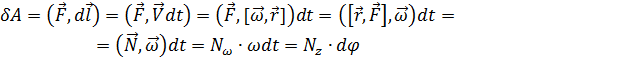
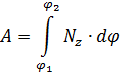
(Опр.) Мощность силы равна отношению работы δA, совершаемой за малый интервал времени dt к величине этого интервала:

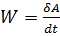
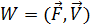
(Опр.) Механическая энергия есть физическая величина, измеряемая запасённой работой, которую способна совершить система тел.

(Опр.) Кинетическая энергия системы материальных точек равна:

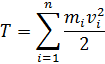
Кинетическая энергия величина аддитивная, скалярная и всегда положительная.

(Опр.) Потенциальная энергия измеряется работой, которую тела системы способны совершить при изменении своей конфигурации (взаимного расположения её частей).

Потенциальная энергия является такой функцией координат U = f(x,y,z), что работа консервативных сил A₁₂^(к) равна разности значений этой функции при изменении положений тел системы (конфигурации системы), т.е. A₁₂^(к) = U₁ – U₂ = -∆U.

Связь силы и потенциальной энергии

1) Как найти потенциальную энергию, если известны действующие консервативные силы F̄(x,y,z)?

Пусть в некоторой точке пространства P₀(x₀,y₀,z₀) потенциальная энергия равна нулю: U(x₀,y₀,z₀) = 0. Тогда для произвольного положения частиц системы P(x,y,z) потенциальная энергия равна:

, а значит

2) Как, зная функцию U(x,y,z) для потенциальной энергии, определить силу?

Для малого перемещения dl ̄ элементарную работу можно записать двумя способами: dA₁₂^(к) = -dU и dA₁₂^(к) = (F̄, dl̄). Приравняв правые части, получаем: (F̄, dl̄) = -dU. Скалярное произведение и полный дифференциал функции U(x,y,z) можно перепивать иначе:

Это равенство говорит о том, что проекции вектора силы в любой точке пространства равны с противоположным знаком частным производным по координатам от потенциальной энергии:

Сам вектор F̄ можно задать таким способом:

Модуль силы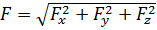

Направление вектора силы (если одну из осей направить по нормали к эквипотенциальной поверхности)

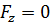
Градиент – вектор, имеющий компоненты и показывающий направление, в котором быстрее всего растёт потенциальная энергия U вблизи данной точки пространства. Сами компоненты вектора градиента дают скорость роста U по координатным направлениям, а вот его модуль определяет скорость в направлении максимального изменения U (в направлении вектора gradU). Таким образом, F определяет изменение потенциальной энергии на единицу длины, в направлении наиболее быстрого изменения энергии. Знак «минус» означает при этом, что сила направлена в сторону убывания потенциальной энергии.

18. Кинетическая энергия при поступательном, вращательном и плоском движении твёрдого тела.

(Опр.) Кинетическая энергия системы материальных точек равна:

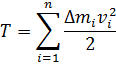
Кинетическая энергия величина аддитивная, скалярная и всегда положительная.

а) При поступательном движении в любой момент времени все элементы тела ∆m_i обладают одной и той же линейной скоростью V ̄₁ = V ̄₂= … = V ̄_i – той же, с которой движется его центр масс – V ̄_c. Поэтому кинетическая энергия поступательно движущегося твёрдого тела равна

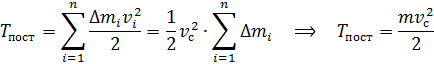
б) При вращательном движении в любой момент времени у всех элементов тела ∆m_i одинаковы угловые скорости. Поэтому

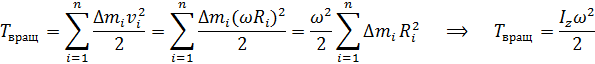
в) Плоское движение можно представить, как совокупность одновременно происходящих поступательного и вращательного. Чтобы найти кинетическую энергию такого движения, удобно вспомнить о понятии мгновенной оси вращения: в каждый момент времени движение представляет собой лишь поворот относительно такой оси, а значит 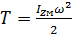. Момент инерции тела относительно мгновенной оси вращения I_zм по теореме Штейнера можно связать с моментом инерции относительно оси, проходящей через центр масс тела I_c:

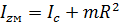
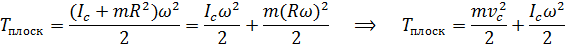
Кинетическая энергия при плоском движении твёрдого тела равна сумме энергии поступательного движения со скоростью центра масс и вращения относительно оси, проходящей через центр масс.

19. Теорема о кинетической энергии. Консервативные и неконсервативные силы. Связь силы и потенциальной энергии.

(Опр.) Кинетическая энергия системы материальных точек равна:

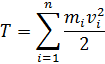
Кинетическая энергия величина аддитивная, скалярная и всегда положительная.

Теорема о кинетической энергии

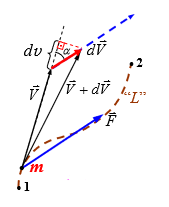
Пусть материальная точка перемещается из точки 1 в точку 2 по произвольной траектории “L”. Найдём элементарную работу действующей на неё силы F ̄ на малом перемещении dl̄:

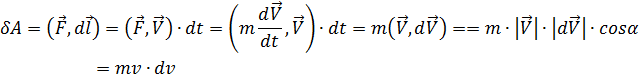
Полученный результат есть не что иное, как дифференциал (малое изменение) кинетической энергии частицы: .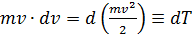

Просуммируем элементарные работы на всех малых участках траектории:

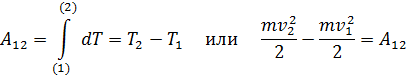
Утверждение теоремы:

Изменение кинетической энергии системы равно работе сил, действующих на тела системы.

Дата добавления: 2019-09-13; просмотров: 173; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!