Определение криволинейного интеграла 2-го рода.
Пусть в области D плоскости xy задана кривая L и функции P ( x , y ) и Q ( x , y ), непрерывные в каждой точке кривой L. Разобьем кривую L произвольно на п частей и обозначим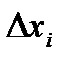 
- проекция i-го участка разбиения на ось x, 
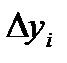- проекция i-го участка на ось у. На каждом участке разбиения произвольно выберем точку 
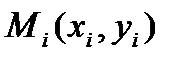и составим интегральную сумму
.
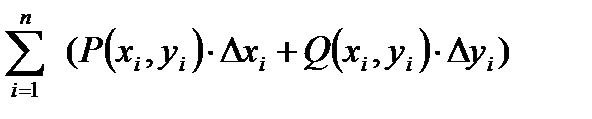Если существует конечный предел полученной интегральной суммы, не зависящий ни от способа разбиения кривой L на части, ни от выбора точек, тогда этот предел называется криволинейным интегралом 2-го рода или интегралом по координатам.
.
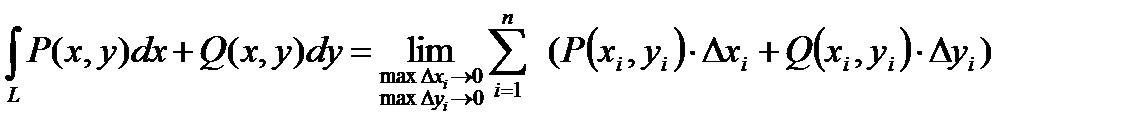Свойства криволинейных интегралов 2-го рода.
1) Криволинейный интеграл 2-го рода зависит от направления интегрирования:
.
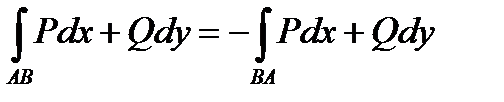2) Если кривая L разбита на части L 1 и L 2, тогда
.
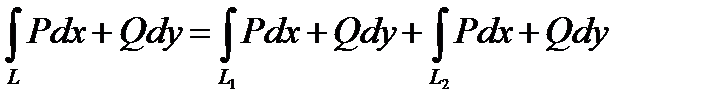3) Криволинейный интеграл можно рассматривать как сумму интегралов
.
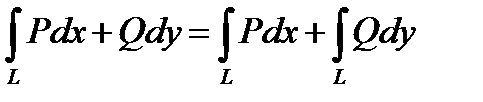1-ый интеграл называется интегралом по координате х, а 2-ой ― по координате у.
4) Если кривая L замкнута, то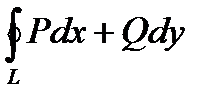 
.
В этом случае обязательно указывается направление интегрирования. Направление интегрирования называется положительным, если при обходе по контуру L область D всегда остается при этом слева, т. е. против часовой стрелки. Если обход совершается по ходу часовой стрелки, то направление интегрирования называется отрицательным.
Вычисление криволинейного интеграла 2-го рода.
1) Пусть кривая L задана параметрически:
, 
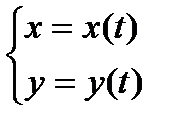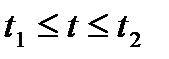. Причем, t 1 соответствует началу кривой, а t 2 – концу кривой.
|
|
|
Рассмотрим интегральную сумму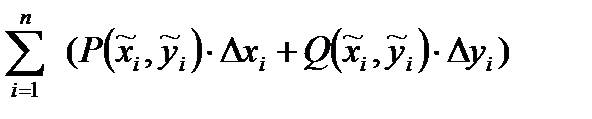 
.
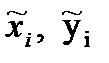- точка, произвольно выбранная на i-ом участке.
Рассмотрим 1-ое слагаемое.
Пусть значение параметра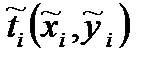 
, тогда функция 
.
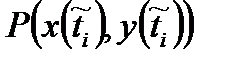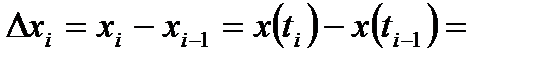(применим теорему Лагранжа)=
.
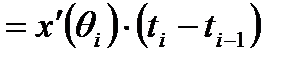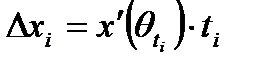, где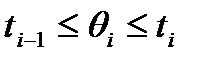 
.
Проведя аналогичные рассуждения для 2-го слагаемого, получим:
.
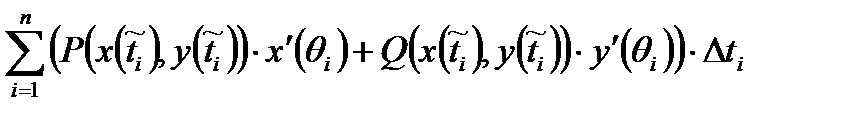Таким образом, получаем равенство:
.
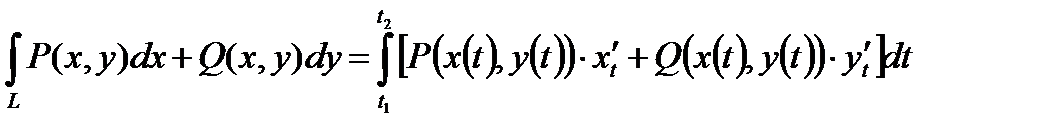2) Пусть кривая L задана в декартовых координатах:
.
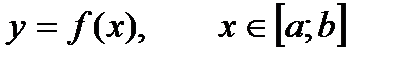Выберем в качестве параметра х.
L :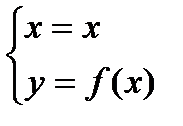 
, 
.
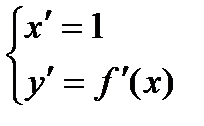Тогда имеет место равенство:
.
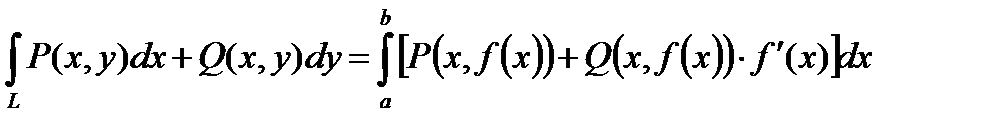Замечание. Кривая L задана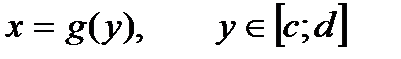 
. Тогда в качестве параметра выберем y .
L :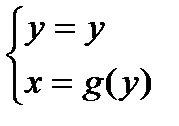 
, 
.
.
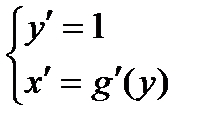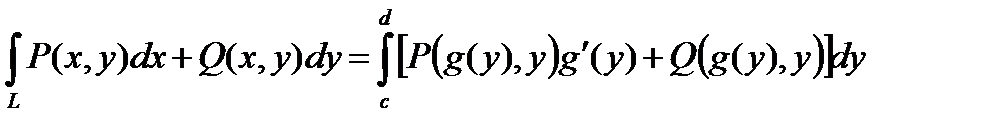Пример. Вычислить криволинейный интеграл 2-го рода по кривой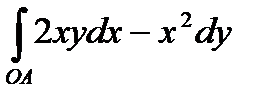 
, где О(0;0), А(2;1).
1) Пусть ОА – прямая соединяющая точки О и А.
, 
.
, 
.
.
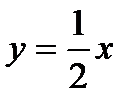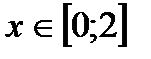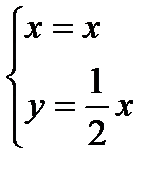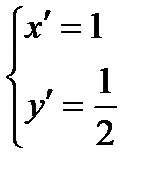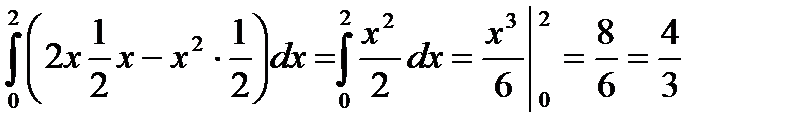2) Пусть ОА ― парабола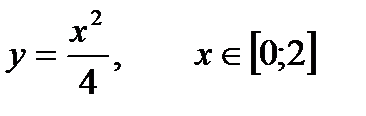 
.
, 
.
.
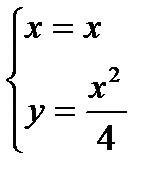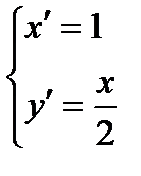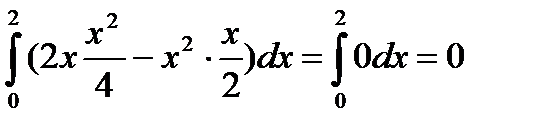Вывод: Криволинейный интеграл 2-го рода зависит не только от функций P и Q и направления интегрирования, но и от формы кривой L.
Пример. Вычислить интеграл по замкнутой кривой L: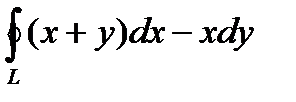 
, где L – окружность 
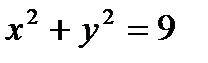, причем обход совершается по часовой стрелке.
Так как обход совершается по часовой стрелке, то обход отрицательный. Запишем уравнение окружности параметрически:
, 
. 
.
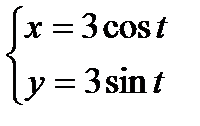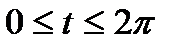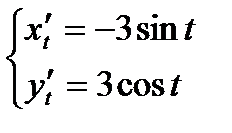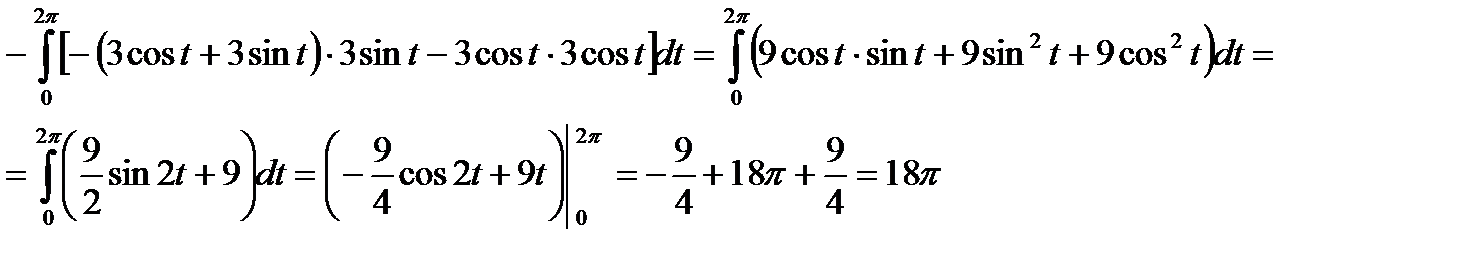
Замечание.
Если кривая L задана в пространстве, то все вычисления производятся аналогично.
|
|
|
Формула Грина.
Эта формула устанавливает связь между криволинейным интегралом 2-го рода по замкнутому контуру L и двойным интегралом по области D, ограниченной этим контуром.
Теорема. Если функции P ( x , y ) и Q ( x , y ) непрерывны вместе со своими частными производными в некоторой области D плоскости ху, ограниченной замкнутым контуром L, тогда справедливо равенство:
,
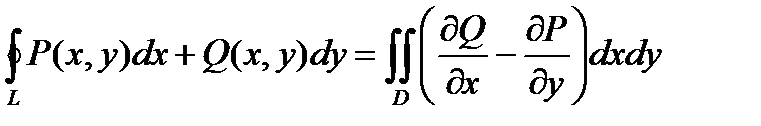причем интегрирование по кривой L происходит в положительном направлении.
Пример. Вычислить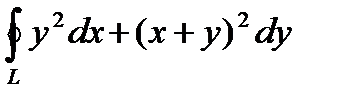 
, где L : ΔABC . A (3;0), B (3;3), C (0;3).
, 
. 
, 
.
.
;
.
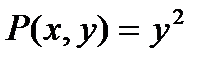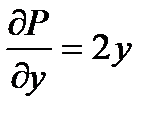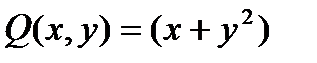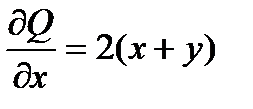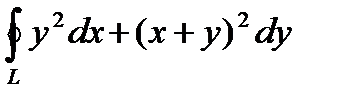
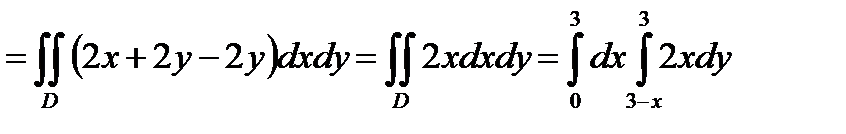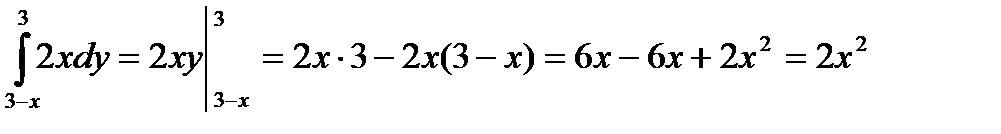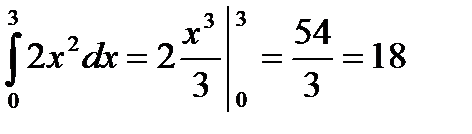Следствие из формулы Грина.
Если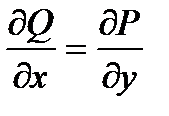 
, тогда справедливы 3 утверждения:
1. 
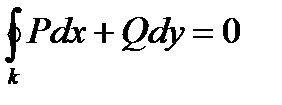, причем замкнутый контур к полностью находится внутри области D.
2. 
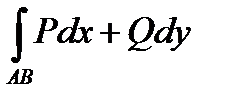не зависит от формы кривой АВ, если и сама кривая, и точки АВ полностью находятся в области D, а зависит только от положения точек АВ.
3. Если подынтегральное выражение является полным дифференциалом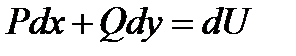 
, тогда можно восстановить саму функцию.
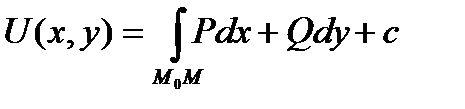, с – произвольная постоянная.
Примеры.
Рассмотрим 2-ое следствие.
Вычислить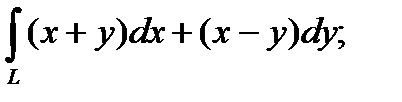 
где кривая L соединяет точки О и А.
L: O(0;0), A(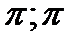 
) .
P=x+y;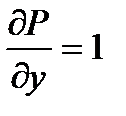 
; Q=x-y; 
.
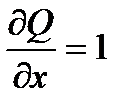1)Пусть L – прямая ОА.
ОА: y = x ,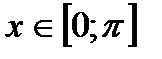 
, 
.
.
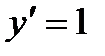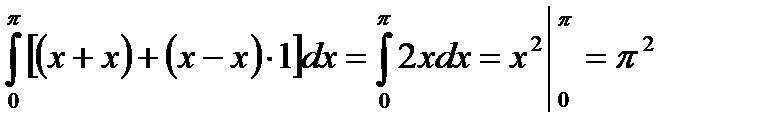2) Пусть кривая L –ломанная ОАВ, В(π;0).
ОВ: y =0,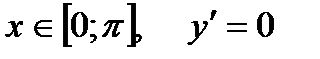 
.
.
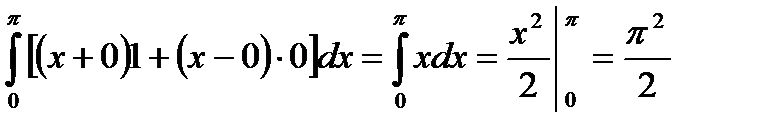BA : x = π ,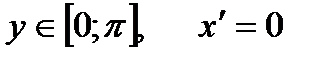 
.
.
.
|
|
|
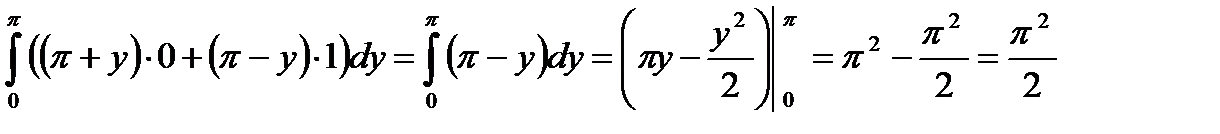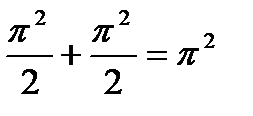3) Пусть кривая L – парабола OA :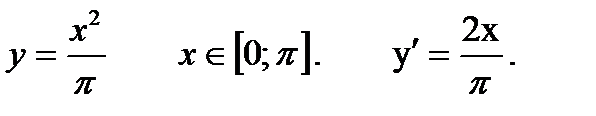 
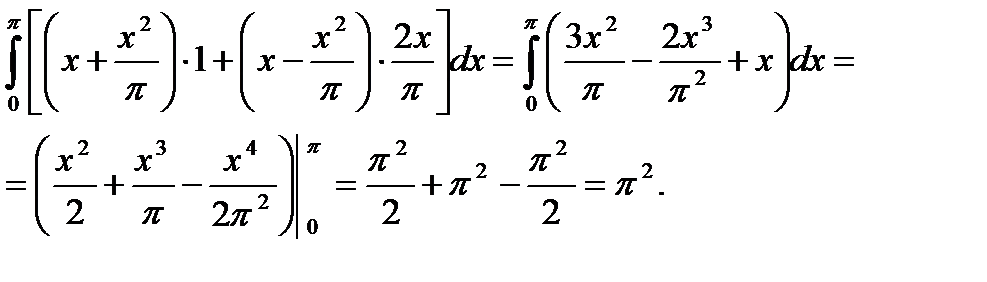
Рассмотрим третье следствие.
Восстановить функцию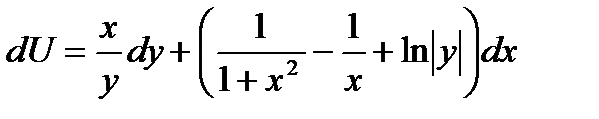 
.
; 
. 
; 
.
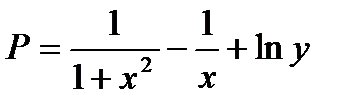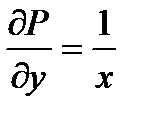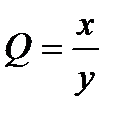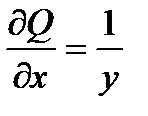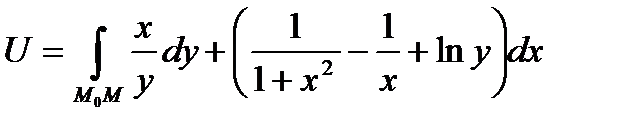
M0(1;1), M(X;Y)
1) 
.
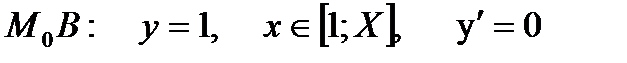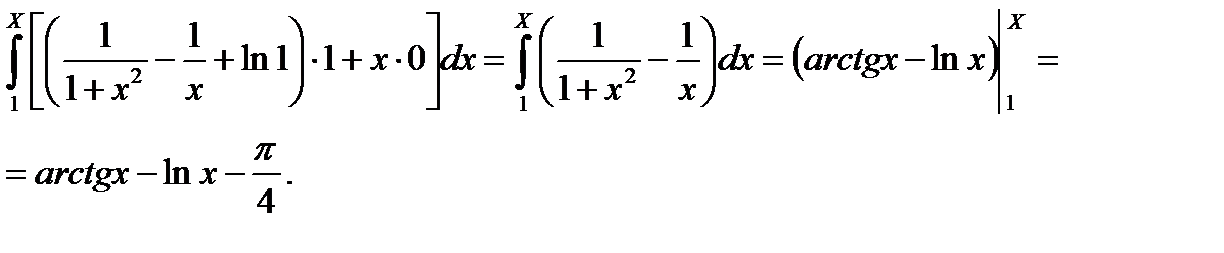
2) 
.
.
;
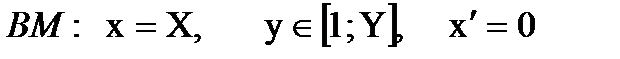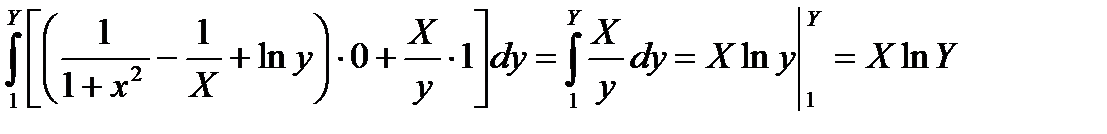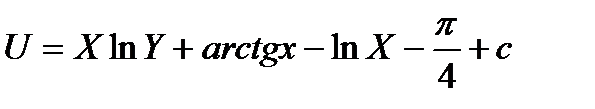Пусть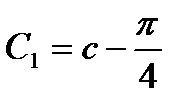 
.
.
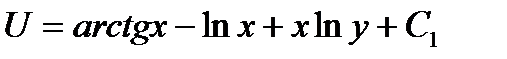Дата добавления: 2019-09-13; просмотров: 144; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!