Задача о массе неоднородного тела.

⇐ ПредыдущаяСтр 3 из 7Следующая ⇒

Пусть дано тело, ограниченное замкнутой поверхностью Т, причем плотность в каждой ее точке зависит от координат этой точки 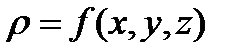. Требуется найти массу данного тела. Разобьем все тело на п частей. Пусть 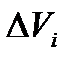- объем i-ой части. В каждой части произвольно выберем точку 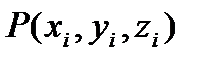и предположим, что плотность каждой i-ой части постоянна и равна значению в точке Р. Тогда масса i-ой части 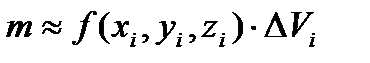. Тогда масса всего тела 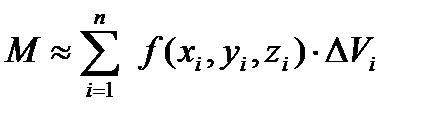. Данное равенство тем точнее, чем на большее число частей мы разбиваем тело .

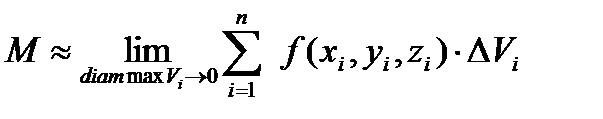Дадим общее определение, не связанное с физическими или геометрическими свойствами.

Определение тройного интеграла.

Пусть дана область Т, в каждой точке которой определена непрерывная функция U = f ( x , y , z ). Разобьем область Т произвольно на п частей и обозначим 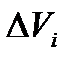- объем i-ой части. На каждом участке разбиения произвольно выберем точку 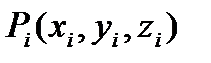и составим интегральную сумму .

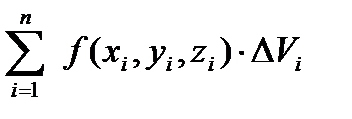Если существует конечный предел интегральной суммы, не зависящий ни от способа разбиения области Т на части, ни от выбора точек P_i, тогда этот предел называется тройным интегралом по области Т от функции f ( x , y , z ).

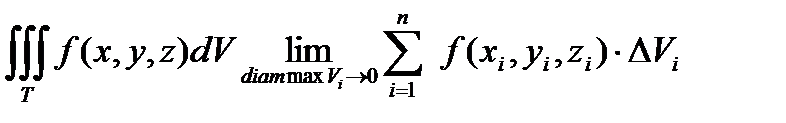, где dV – элемент объема.

Свойства тройных интегралов.

1. .

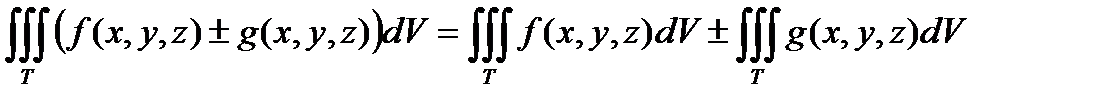2. .

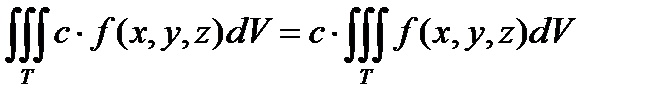3. Если .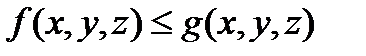

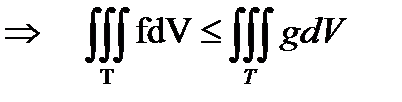4. .

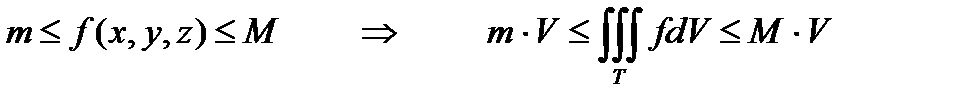5. точка 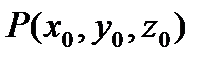такая, что выполняется равенство

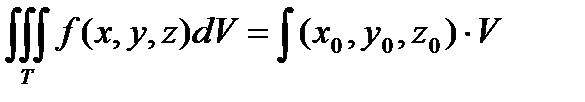, где V – объем области Т.

6. Область Т разбита на не пересекающиеся части Т₁ и Т₂ , тогда

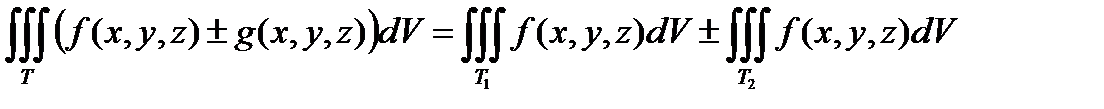Вычисление тройного интеграла в декартовых координатах.

Пусть дан 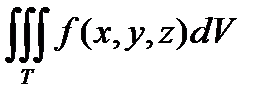. Разобьем область Т плоскостями параллельными координатным плоскостям. В результате каждая часть разбиения будет являться параллелепипедом.

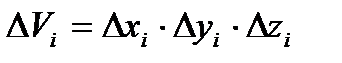. Тогда .

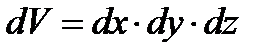Таким образом, получаем .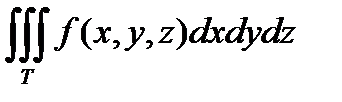

Область D является правильной в направлении оси z, если любая прямая параллельная этой оси пересекает границу тела не более чем 2 раза. Тело может быть правильным также в направлении оси x и оси y.

Пусть область D будет правильной в направлении оси z, т.е. всю поверхность, ограничивающую данную область можно разбить на 2 части: нижнюю z ₁ = f ₁ ( x , y ) и верхнюю z ₂ = f ₂ ( x , y ). Область D – проекция тела на плоскость xy.

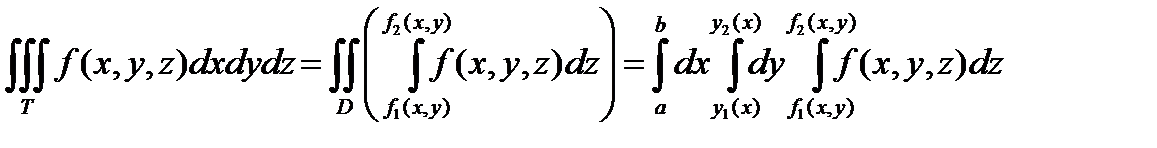― трехкратный интеграл.

Причем, 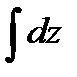- называется внутренним, 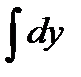- средним, 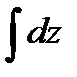- внешним.

Замечание.

1) Если тело является правильным в направлении другой оси, то трехкратный интеграл изменится соответствующим образом.

2) Если область Т не является правильной в направлении ни одной оси, тогда область разбиваем на части таким образом, чтобы каждая часть была правильной в направлении хотя бы одной оси.

Пример. Вычислить тройной интеграл 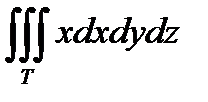, где T : x =0, y =0, z =0, y = x , x + z =1.

Спроецируем тело на плоскость xz .

;

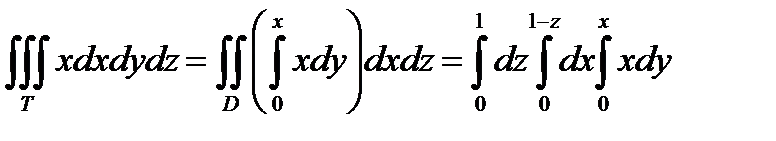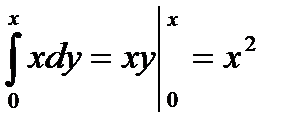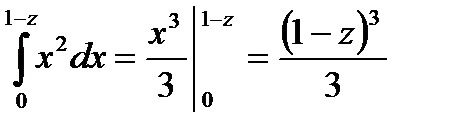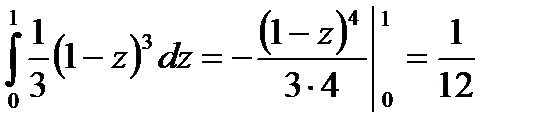Замена переменной в тройном интеграле.

Пусть дан .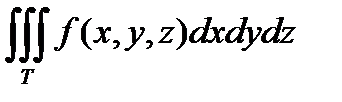

Пусть .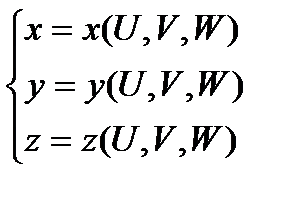

Если для каждой тройки xyz существует единственное решение U , V , W, тогда справедливо равенство:

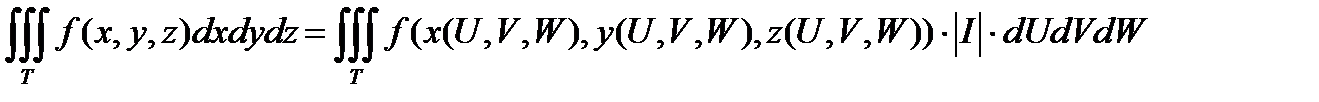где 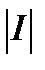- якобиан перехода:

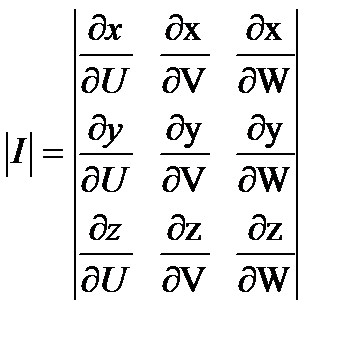Дата добавления: 2019-09-13; просмотров: 520; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!