Определение криволинейного интеграла 1-го рода.

Пусть на плоскости xy дана некоторая область D. Пусть в этой области дана гладкая кривая, в каждой точке которой определена функция 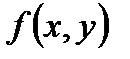. Разобьем всю кривую произвольным образом на n частей точками  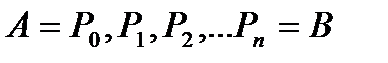и обозначим  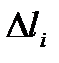- длина i-го участка разбиения. На каждом участке разбиения произвольно выберем точку  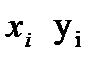и составим интегральную сумму .

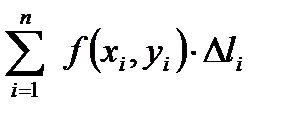Если существует конечный предел интегральной суммы, не зависящий ни от способа разбиения кривой на части, ни от выбора точек, тогда он называется криволинейным интегралом 1-го рода или криволинейным интегралом по длине дуги.

.

 

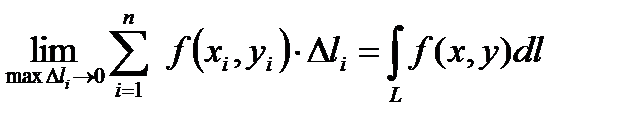Свойства криволинейных интегралов 1-го рода.

1. .

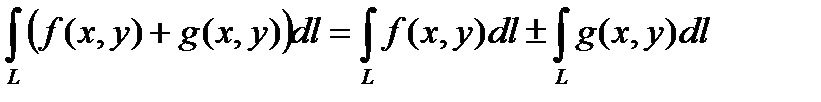2. .

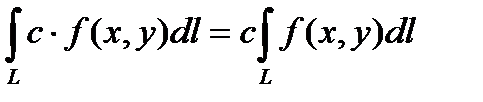3. Если кривая L разбита на 2 части l ₁  и l ₂, тогда справедливо равенство

.

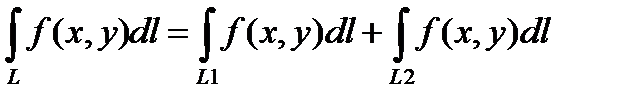4. Значение интеграла не зависит от порядка интегрирования

.

 

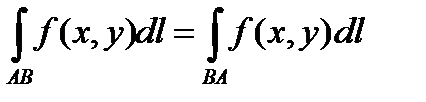Вычисление криволинейного интеграла 1-го рода.

 

1) Кривая L задана параметрически:

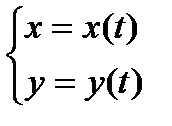 , причем .

t ₁ – соответствует началу кривой, т. е. точке A, t ₂ – концу кривой B.

Из приложений определенных интегралов .

Тогда справедливо равенство:

.

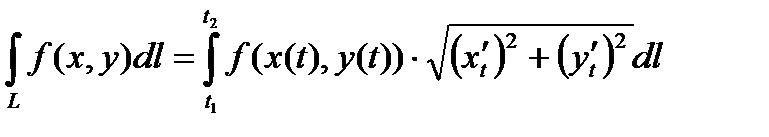Таким образом, криволинейный интеграл 1-го рода сводится к определенному интегралу.

2) Кривая L задана в декартовых координатах:

.

Тогда выберем в качестве параметра x:

, , .

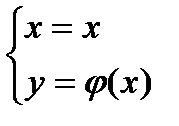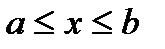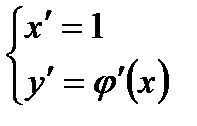Получаем равенство:

.

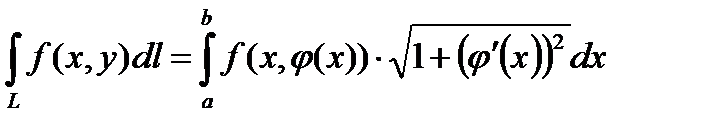Замечание.

Если кривая L задана , тогда в качестве параметра выбирается y.

, .

.

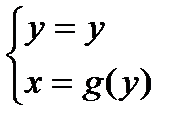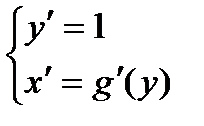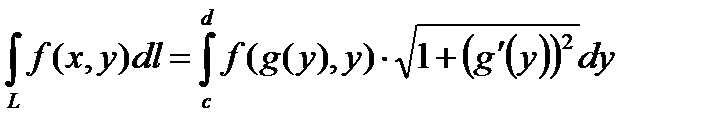3) Кривая L задана в полярных координатах:

.

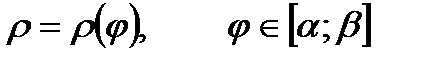Связь между декартовыми и полярными координатами: .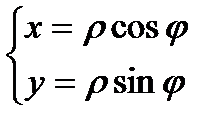

Учитывая, что 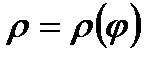, получаем .

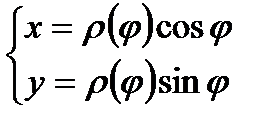Т. е. параметром является φ. Найдем дифференциал дуги.

.

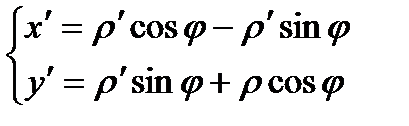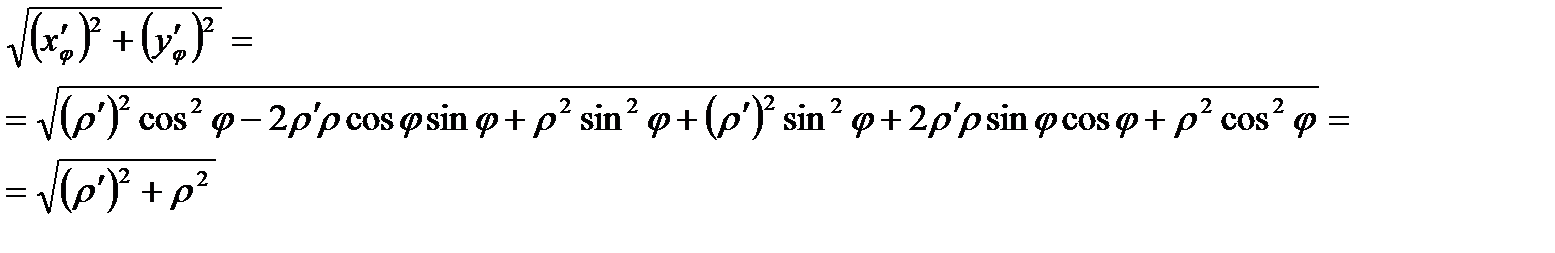Тогда справедливо равенство:

.

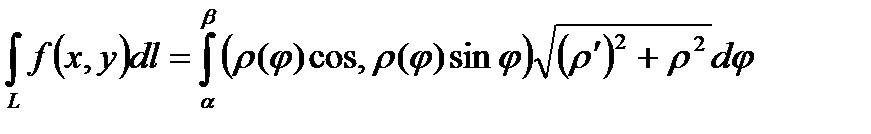Замечание.

Кривая L на плоскости может быть замкнутой, тогда криволинейный интеграл 1-го рода обозначается следующим образом: .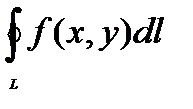

Пример. Вычислить криволинейный интеграл 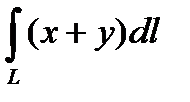, L – контур треугольника АВО.

L : ΔABO , A (1;0), B (0;1), O (0;0).

Построим контур L.

Разобьем криволинейный интеграл на части: .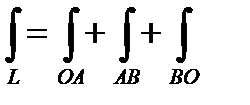

1. OA: y=0, , .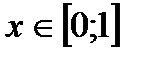

.

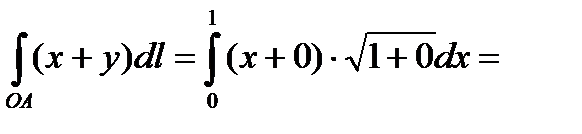
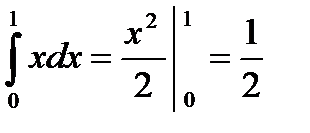2. AB: x+y=1, x=1-y, .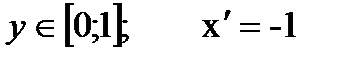

.

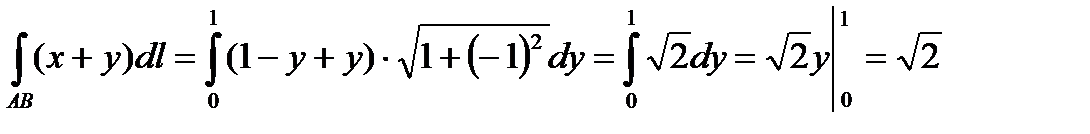3. BO: .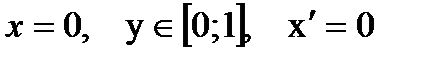

.

.

 

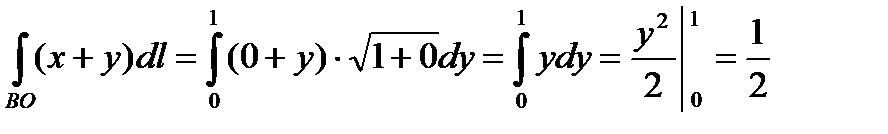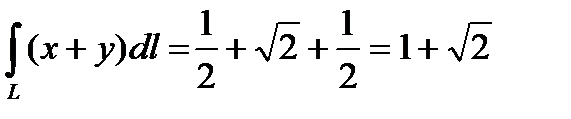Применение криволинейного интеграла 1-го рода.

1. Вычисление массы кривой L с переменной плотностью.

.

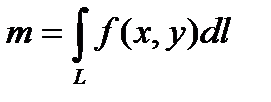2. Вычисление площади боковой поверхности цилиндрического тела.

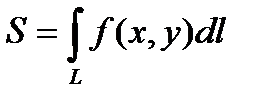, где z = f ( x , y ) – поверхность, ограничивающая цилиндрическое тело сверху, L ― кривая на плоскости xy , образованная цилиндрической поверхностью.

3. Вычисление длины дуги кривой AB .

.

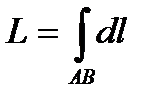Пример. Вычислить массу дуги окружности 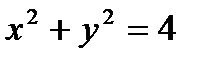 (ее верхней части), если плотность в каждой точке равна у.

Плотность .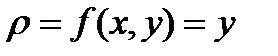

L – верхняя часть окружности .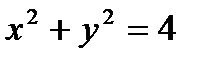

Масса находится по формуле .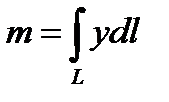

Построим контур L:

Запишем уравнение окружности параметрически:

, . .

.

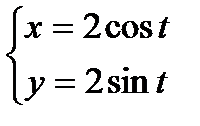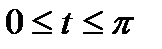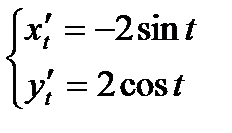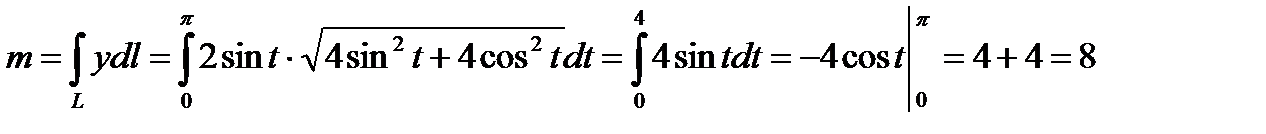Замечание.

Если кривая L задана в пространстве, то выводы все аналогичны, как и для плоского случая.

Пример. Вычислить криволинейный интеграл 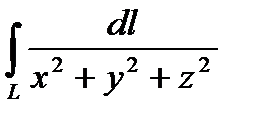, L – первый виток винтовой линии.

L : 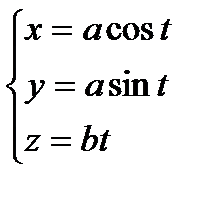 , , 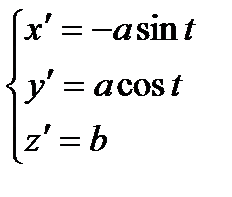, 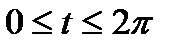т. к. берем 1 виток.

.

 

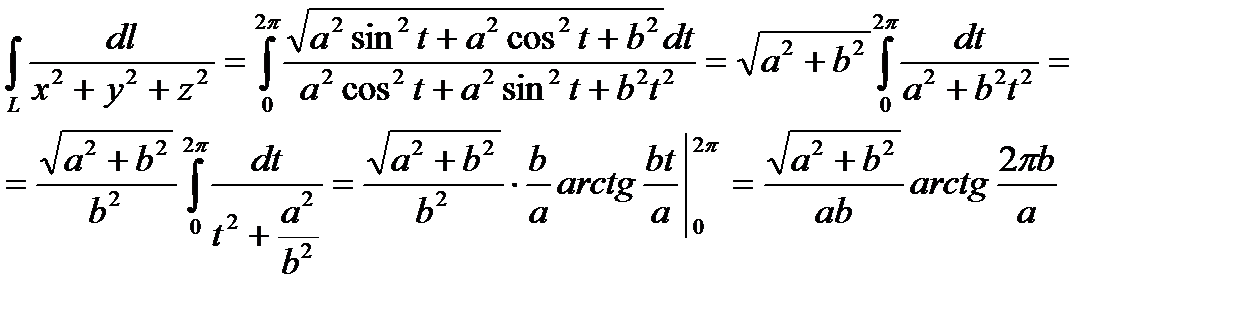Задача о работе силового поля.

 

Пусть в некоторой области D на плоскости xy действует силовое поле, т. е. в каждой точке этой области действует сила, величина и направление которой зависит от координат этой точки .

Пусть под действием данной силы точка перемещается вдоль кривой L с началом в точке A и с концом в точке B. Требуется найти работу, затраченную силой на перемещение этой точки вдоль кривой L.

Разобьем кривую L на п частей точками A = M ₀ , M ₁ ,…, M_n = B и рассмотрим i -ый участок разбиения ( M_{i -1} , M_i ).

Предположим, что на i-ом участке разбиения сила постоянна и принимает значение в точке M_{i -1}: .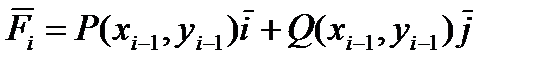

Т. к. длина i-го участка разбиения достаточно мала, будем считать, что перемещение происходит вдоль вектора 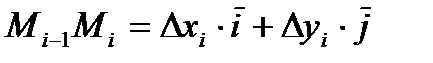. Тогда работа на i-том участке – это скалярное произведение вектора силы на вектор перемещения.

.

.

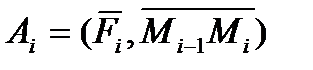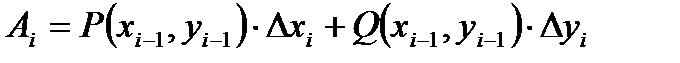Тогда работа по перемещению вдоль всей кривой L от A до В:

.

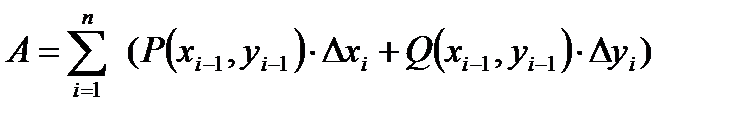Данное равенство тем точнее, чем на большее число частей мы разбиваем кривую L, тогда работа:

.

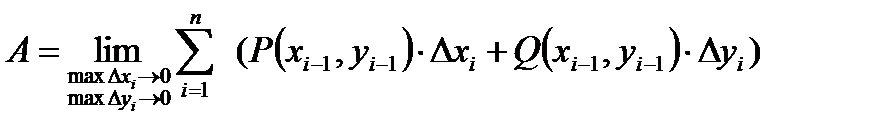Задач, приводящих к подобным пределам, достаточно много в физике, химии и других областях.

 

---

Дата добавления: 2019-09-13; просмотров: 244; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!