Тройной интеграл в цилиндрических координатах.
Пусть дан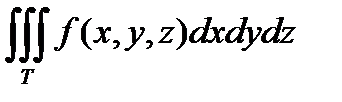 
.
Пусть область Т будет правильной в направлении оси z, тогда цилиндрические координаты имеют вид:
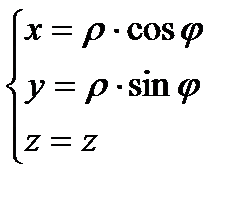, где 
.
Вычислим якобиан перехода:
.
.
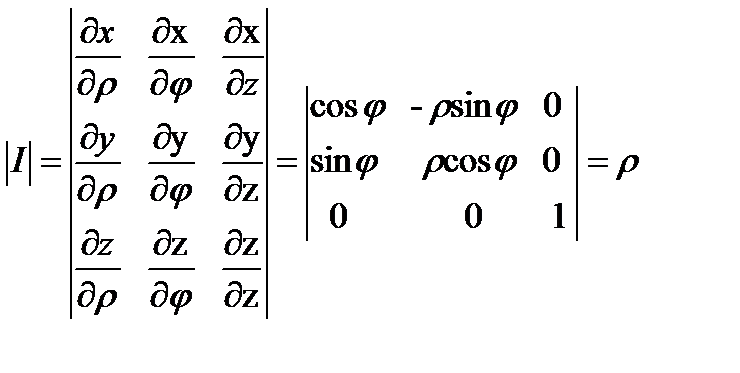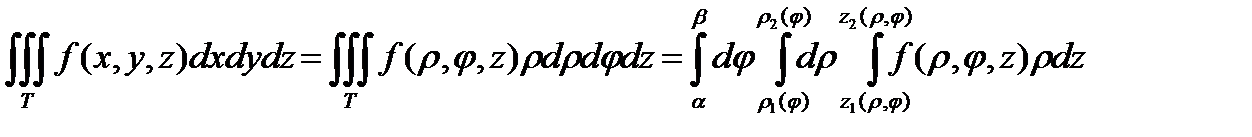Замечание.
1) Переходить к цилиндрическим координатам удобно в том случае, когда область D (проекция тела Т на координатную плоскость) связана с дугами окружности.
2) Если область D правильная в направлении оси x или y, тогда формула изменит свой вид.
Пример. Вычислить тройной интеграл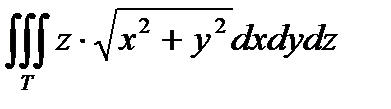 
, где T : x 2 + y 2 =2 x , y =0, z =0, z =1.
( x -1)2+ y 2 =1 – эллиптический цилиндр. Направляющая – окружность с центром в точке (1;0), радиус – 1, образующие параллельны оси z.
Перейдем к цилиндрическим координатам:
.
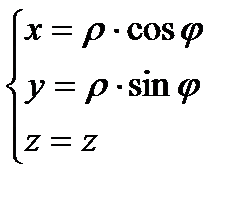Подынтегральная функция будет иметь вид: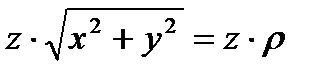 
.
Уравнение цилиндра в цилиндрических координатах: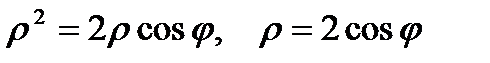 
.
.
;
;
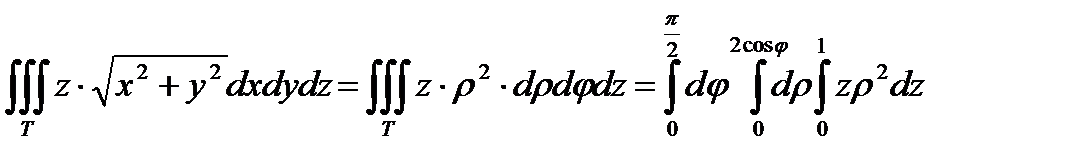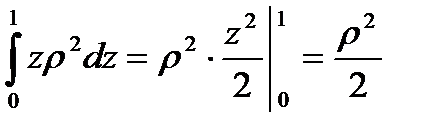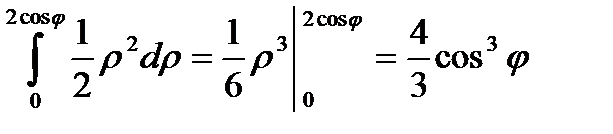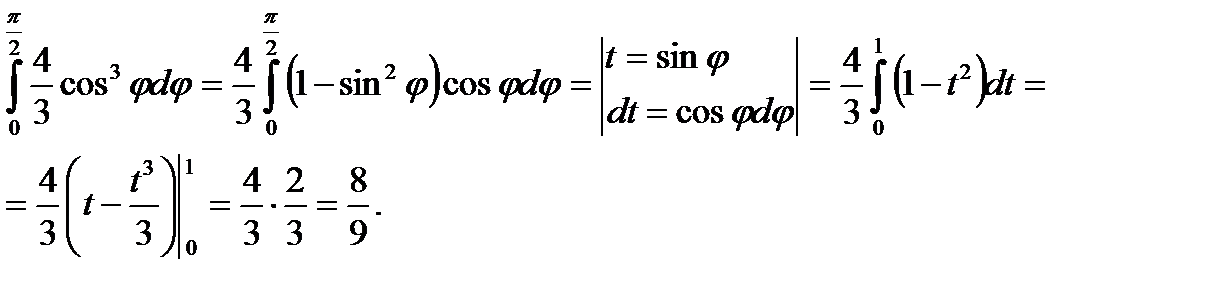
Тройной интеграл в сферических координатах.
Пусть дан .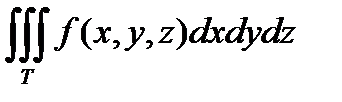
Связь между декартовыми и сферическими координатами (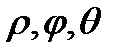 
):
, где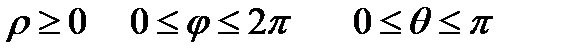 
.
Вычислим якобиан перехода:
.
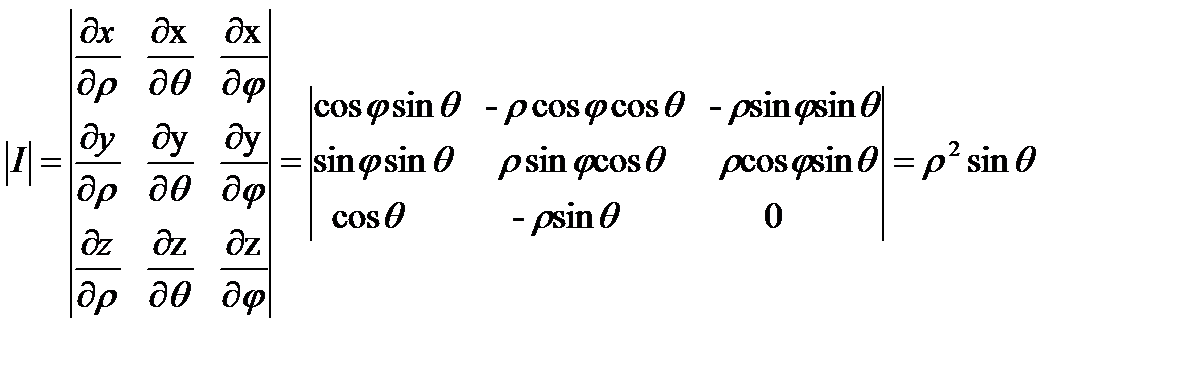Тогда имеет место равенство:
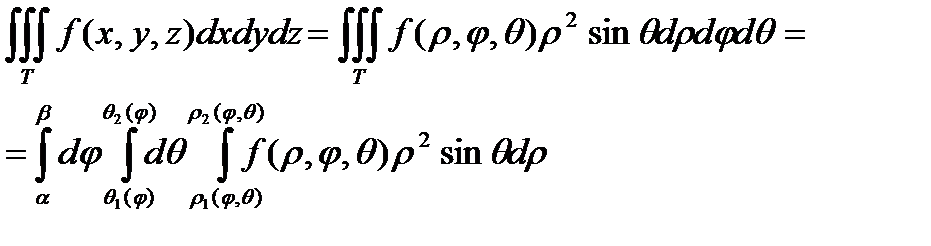
Замечание.
К сферическим координатам удобно переходить в том случае, если поверхности ограничивающие область Т являются сферой.
Пример. Вычислить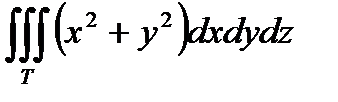 
, где T : x 2 + y 2 + z 2 =1, z =0, z >0.
Построим область T :
Перейдем к сферическим координатам.
Уравнение сферы в новых координатах:
.
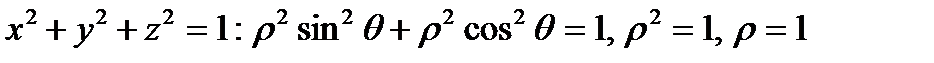Подынтегральная функция в сферических координатах:
.
.
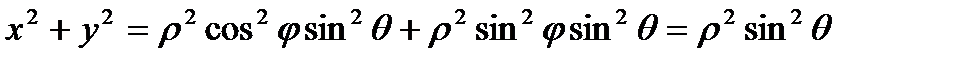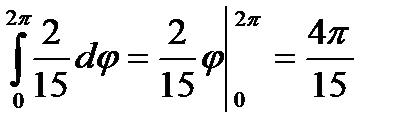Применение тройных интегралов.
1. Вычисление массы тела, ограниченного областью Т и имеющего переменную плотность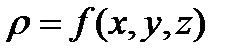 
.
|
|
|
.
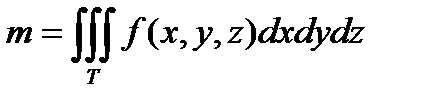2. Вычисление объема тела, ограниченного областью Т.
.
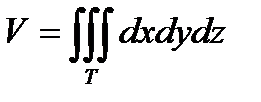Пример. Найти объем тела, ограниченного областью T : ( z -2)2= x 2 + y 2 – конус, z =0.
Объем тела находится по формуле: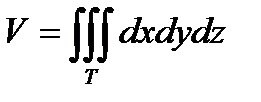 
.
Построим область T .
x 2 + y 2 =4 – линия пересечения конуса и плоскости xy .
Перейдем к цилиндрическим координатам:
.
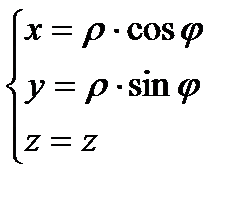Найдем уравнение конуса в цилиндрических координатах:
( z -2)2= x 2 + y 2 ( z -2)2= ρ 2 
, 
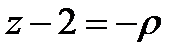- нижняя часть конуса, 
.
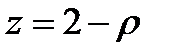Уравнение границы области D в цилиндрических координатах: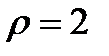 
.
.
;
;
.
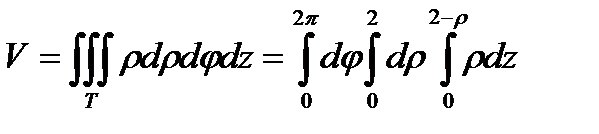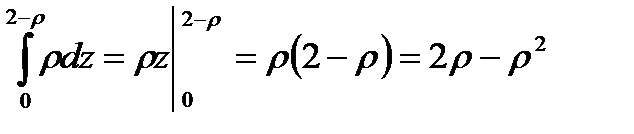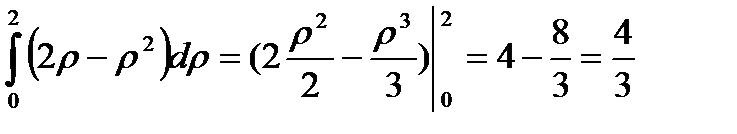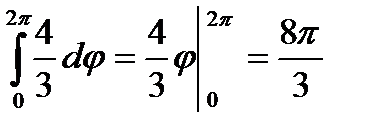Криволинейные интегралы.
Задача о массе неоднородной кривой.
Пусть на плоскости xy дана кривая l с началом в точке A и с концом в точке B. Пусть в каждой точке кривой плотность определена как функция координат этой точки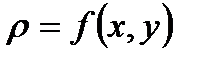 
. Требуется найти массу данной кривой.
Всю кривую разобьем на п частей точками так, чтобы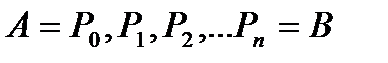 
. Обозначим 
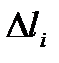- длина i-го участка разбиения. На каждом промежутке разбиения произвольным образом выберем точку 
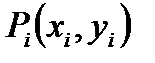. Предположим, что плотность на каждом участке разбиения постоянна и равна значению в точке 
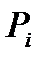. Тогда масса i-го участка 
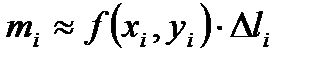. Таким образом, масса всей кривой 
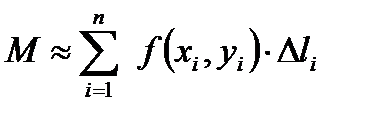. Данное равенство тем точнее, чем на большее число частей мы разбиваем кривую.
|
|
|
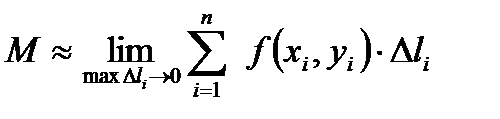
Замечание.
Подобные задачи возникают не только в физике, но и в геометрии. Например, задача о площади боковой поверхности цилиндрического тела.
Дадим общее определение, не связанное с физическими и геометрическими свойствами.
Дата добавления: 2019-09-13; просмотров: 176; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!