Интегральная форма теоремы об изменении кинетической энергии
Применение этой формы теоремы об изменении кинетической энергии наиболее эффективно при решении задач, в которых необходимо определить зависимость какой-либо скорости (линейной или угловой) от перемещений, совершенных точками механической системы, причём, предоставляется возможность вычисления работы сил без детального кинематического анализа движения механической системы. Например, при наличии потенциальных сил, можно вычислить работу сил, имея информацию только о начальном и конечном состояниях системы.
Пример 5.1
Колесо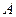 
скатывается без скольжения по наклонной плоскости, образующей угол 
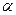с горизонтом (Рис. 5.1). К оси колеса привязан трос, переброшенный через неподвижный блок 
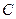и прикрепленный к грузу 
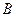, поднимающемуся по наклонной плоскости, образующей угол 
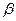с горизонтом. В начальный момент система находилась в покое. Колесо и блок представляют собой сплошные однородные диски с массами 
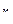и и радиусами 
и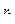 
соответственно. Масса груза равна 
. Коэффициент трения между грузом и наклонной плоскостью равен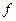 
. Определить зависимость скорости оси колеса 
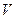от числа оборотов 
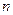блока .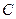
|
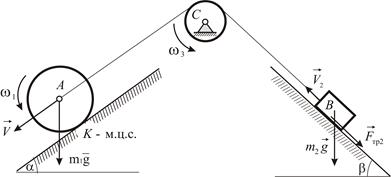
| Рис. 5.1 |
Начальная кинетическая энергия системы равна нулю. Система состоит из трех абсолютно твердых тел и нерастяжимого троса, поэтому суммарная работа всех внутренних сил также равна нулю. При таких условиях кинетическая энергия системы в любой момент времени равна сумме работ внешних сил, совершенных к этому моменту времени.
|
|
|
Найдем кинетическую энергию системы. Вычисляем кинетическую энергию системы:
.
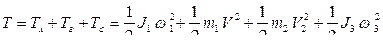Учитывая кинематические соотношения
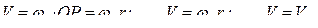
получаем: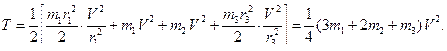 
|
| Рис. 5.2 |
При вычислении работы внешних сил заметим, что сила трения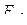 
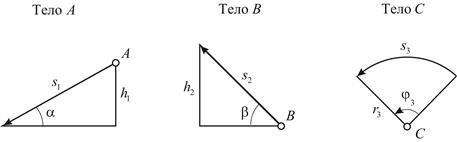
работу не совершает, поскольку точка приложения этой силы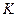 
в любой момент времени имеет нулевую скорость. Перемещения точек связаны между собой соотношениями (Рис. 5.2):
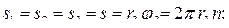
Вычислим работу внешних сил:
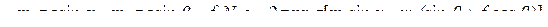
Возвращаясь к теореме об изменении кинетической энергии, находим:
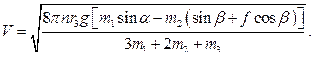
Применение теоремы об изменении кинетической энергии к определению реакций связей
Реакции связей зависят от движения точек механической системы, которое заранее неизвестно. Однако можно привести множество задач, в которых именно теорема об изменении кинетической энергии в дифференциальной или интегральной форме предоставляет возможность достаточно просто определить кинематические характеристики механической системы. Это замечание относится, в первую очередь, к механическим системам с одной степенью свободы.
|
|
|
Пример 5.2
По рельсам, положенным по пути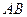 
и образующим затем петлю в виде кругового кольца 
радиуса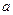 
, скатывается тележка массы 
(Рис. 5.3). Пренебрегая трением, определить, с какой высоты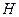 
нужно пустить тележку без начальной скорости, чтобы она могла пройти всю окружность кольца, не отрываясь от него. Определить давление тележки на кольцо в любой точке 
.
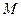Положение точки 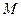на кольце будем задавать углом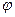 
. В соответствии со вторым законом Ньютона
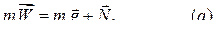
Траектория точки 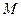на участке — окружность. Интересующая нас сила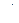 
направлена по нормали к этой окружности. Поэтому запишем уравнение 
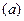в проекциях на главную нормаль к траектории. Учитывая формулы (1.4), получаем:
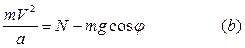
Остается определить скорость точки. Это в данном случае удобно сделать при помощи теоремы об изменении кинетической энергии.
Заметим, что нормальная реакция не совершает работу, т.к. сила 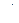всегда направлена перпендикулярно скорости точки приложения силы. Работу совершает только сила тяжести. Поэтому в рассматриваемом случае имеем:
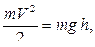где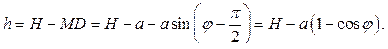 
|
|
|
Отсюда:
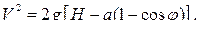
Подставляя полученный результат в уравнение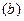 
, находим:
|
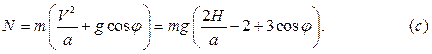
| Рис. 5.3 |
Как видно из решения (с), давление на опорное кольцо минимально в верхней точке окружности при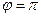 
:
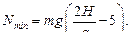
Чтобы тележка не отделялась от опоры в верхней точке, должно выполняться условие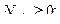 
отсюда:
Пример 5.3
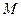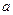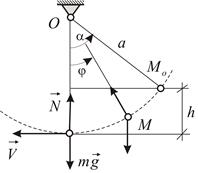
Шарик массы привязан к концу нерастяжимой нити длины , другой конец которой закреплен. Нить отклонили от вертикали на угол 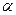и отпустили шарик без начальной скорости (Рис. 5.4). Определить скорость шарика при прохождении им нижней точки траектории, а также натяжение нити в этом положении.
Для решения задачи используем дифференциальное уравнение движения точки в проекциях на главную нормаль к траектории (1.4):
которое в нижней точке траектории принимает вид
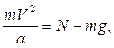
и теорему об изменении кинетической энергии:
|
| Рис. 5.4 |
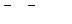или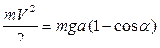 
поскольку в рассматриваемом случае начальная кинетическая энергия равна нулю, а работу совершает только сила тяжести
|
|
|
Таким образом,
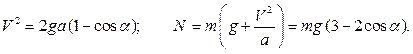
Пример 5.4
Тело 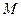, масса которого равна , скользит по гладкой цилиндрической поверхности радиуса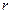 
. К телу прикреплена пружина жесткости 
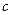, второй конец которой прикреплен к шарниру 
. Длина недеформированной пружины, массой которой можно пренебречь по сравнению с массой тела, равна 
. Расстояние от шарнира до цилиндрической поверхности 
(Рис. 5.5). Определить скорость тела и его давление на цилиндрическую поверхность в момент прохождения положения статического равновесия, если в начальный момент времени тело смещено от положения равновесия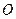 
по дуге окружности на центральный угол 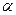и отпущено без начальной скорости.
На тело действуют две потенциальные силы – сила реакции пружины 
и сила тяжести 
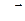, а также реакция 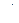гладкой поверхности, работа которой равна нулю. Следовательно, имеет место закон сохранения полной механической энергии.
В начальном положении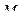 
имеем
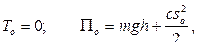
где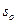 
– начальное удлинение пружины, 
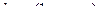– высота точки 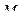над нулевым уровнем, проходящим через точку 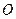. Из прямоугольного треугольника 
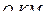получаем:
.
|
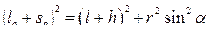| Рис. 5.5 |
Отсюда:
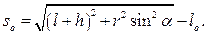
В момент прохождения телом положения статического равновесия имеем:
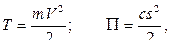где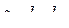 
Подставляя найденные величины в закон сохранения полной механической энергии
,
получаем:
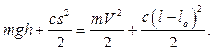
Отсюда:
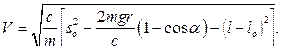
Для определения давления тела на опорную поверхность используем теорему о движении центра масс тела в проекциях на главную нормаль в нижней точке траектории:
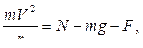
где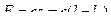 
– сила реакции пружины. Отсюда получаем давление тела на поверхность, равное по модулю реакции:
.
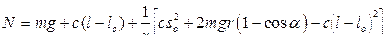Дата добавления: 2019-09-02; просмотров: 325; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!