ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ

Пример 2.1

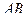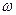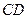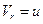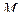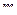Балка  равномерно вращается с угловой скоростью  вокруг вертикальной оси , образуя с ней прямой угол. По балке движется с постоянной относительной скоростью  ползун  массы  (Рис. 2.1). Определить изгибающий момент относительно оси вращения, действующий на балку. При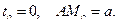  

 

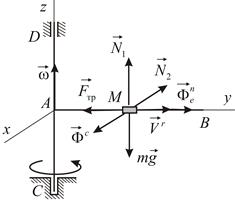
Рис. 2.1

На ползун действуют сила трения 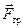, сила тяжести  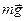и нормальная реакция балки 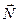, которую разложим на две составляющие  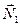и 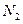. По условию ползун движется равномерно и прямолинейно, так что его относительное ускорение равно нулю. Искомый изгибающий момент создает приложенная к балке горизонтальная составляющая реакции ползуна, которая (в соответствии с третьим законом Ньютона) равна по модулю и противоположна по направлению силе 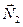. Записывая дифференциальное уравнение относительного движения ползуна в проекциях на ось 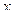, получаем:

  

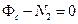
и, следовательно,

                                                                                           

 

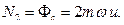
Остается вычислить плечо силы, которое равно координате 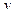 ползуна. Учитывая, что ползун движется относительно балки равномерно, получаем:

 

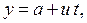
где 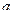 – начальное расстояние ползуна от оси вращения. Таким образом, модуль изгибающего момента относительно оси вращения равен

 

                                               

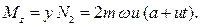
Пример 2.2

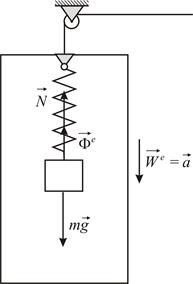
Кабина лифта опускается по вертикали с ускорением 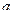. Груз массы  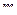подвешен к концу пружины, закрепленной в кабине (Рис. 2.2). Груз покоится по отношению к кабине. Каково показание пружинных весов?

 

Рис. 2.2

Условие относительного равновесия имеет вид:

 

                                                        

 

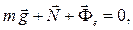
где 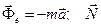 – реакция пружины. В проекциях на вертикальную ось получаем:

 

 

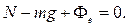
Отсюда

 

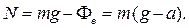
Если лифт поднимается с тем же ускорением, то

 

 

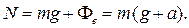
С точки зрения наблюдателя, находящегося в лифте и не знающего о его движении, наблюдаемое уменьшение или увеличение веса груза можно объяснить изменением интенсивности поля тяготения, в котором находится груз.

 

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

 

Из сборника задач И.В.Мещерского: 26.6; 26.7; 26.9; 26.10; 26.27; 27.9; 27.12; 27.13; 27.16; 27.18; 27.22; 27.30; 27.31.

 

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-26.

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

ЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ

Пример 3.1

 

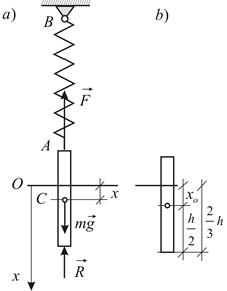
Однородный цилиндр веса 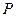, радиуса  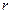и высоты  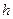подвешен на пружине 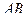, верхний конец которой  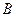закреплен; цилиндр погружен в воду (Рис. 3.1). В положении равновесия цилиндр погружается в воду на половину своей высоты. В начальный момент цилиндр был погружен в воду на 2/3 своей высоты и затем без начальной скорости пришел в движение по вертикальной прямой. Считая жесткость пружины равной 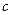, и предполагая, что действие воды сводится к добавочной архимедовой силе, определить движение цилиндра. Принять удельный вес воды равным .

 

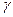Цилиндр движется поступательно. Положение цилиндра будем определять положением его центра масс 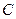. Направим ось  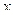вертикально вниз, приняв за начало точку 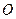, расположенную на поверхности воды, т.е. в равновесном положении точки 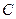. Помимо силы тяжести на цилиндр действуют упругая сила  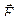и архимедова сила 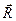, направленная вверх и пропорциональная объему погруженной части цилиндра. Дифференциальное уравнение движения, записанное в проекциях на ось 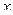, имеет вид:

 

Рис. 3.1

 

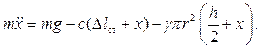
В положении равновесия цилиндр погружен в воду на половину своей высоты, следовательно:

                                                                             

 

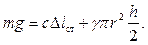
С учетом условия статического равновесия дифференциальное уравнение движения цилиндра представляется в виде:

 

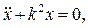
где

 

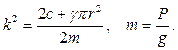
Общее решение полученного дифференциального уравнения имеет вид:

 

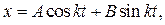
 Остается записать начальные условия. Начальная скорость равна нулю; для начального смещения точки 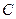 из равновесного положения получаем (Рис. 3.1 ):

 

                                                         

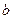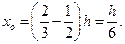
Окончательно получаем: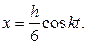

Пример 3.2

 

При равномерном спуске груза массы 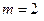т со скоростью 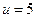м/с произошла неожиданная задержка верхнего конца троса, на котором опускался груз, из–за защемления троса в обойме блока (Рис. 3.2). Пренебрегая массой троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса 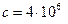Н/м.

По условию груз опускается равномерно, следовательно, приложенные к нему силы уравновешены. В момент начала колебаний груз находится в положении статического равновесия и имеет заданную скорость. Таким образом, начальные условия для задачи о колебании груза имеют вид:

                                      при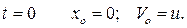   

Составим дифференциальное уравнение движения

 

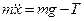             где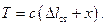           

 

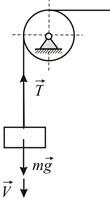
Рис. 3.2

Учитывая условие статического равновесия, получаем

 

 

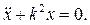
Решение при заданных начальных условиях записывается в виде:

 

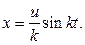
Возвращаясь к дифференциальному уравнению движения, находим силу натяжения троса:

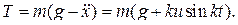
Если 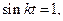 то

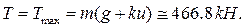
Разобранный пример примечателен в том отношении, что ясно показывает значение динамических нагрузок. Как видно они могут многократно превосходить нагрузки статические.

 

Пример 3.3

 

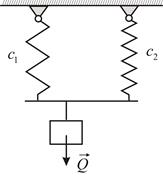
Груз весом 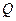 прикреплен к подвеске, состоящей из двух параллельно включенных пружин так, что удлинения пружин, обладающих заданными коэффициентами жесткост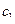и  и 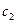, одинаковы (Рис. 3.3). Определить жесткость  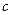эквивалентной пружины.

Период и частота колебаний выражаются через статическую деформацию:

 

 

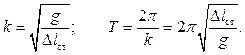
Поскольку период эквивалентной пружины должен совпадать с периодом колебаний тела, подвешенного к системе пружин, статическая деформация эквивалентной пружины должна равняться статической деформации заданной системы, т.е.

 

.

 

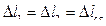Рис. 3.3

 

Запишем условия статического равновесия для каждой из трех пружин:

 

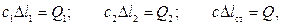
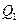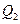где  и  — нагрузка, приходящаяся на каждую из пружин. Эти нагрузки связаны соотношением:

 

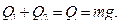
Учитывая, что удлинения пружин одинаковые, получаем:

 

 

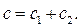
Пример 3.4

 

Определить коэффициент жесткости 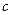 пружины, эквивалентной двойной пружине, состоящей из двух последовательно включенных пружин с разными коэффициентами жесткост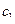и  и 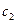 (Рис. 3.4).

 

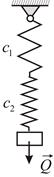
Рис. 3.4

Запишем условия статического равновесия для каждой из трех пружин:

 

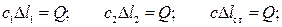
поскольку на каждую из пружин приходится нагрузка, равная весу груза. Статическое удлинение эквивалентной пружины складывается из удлинений пружин, составляющих подвеску:

 

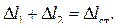     Отсюда: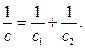      

 

Пример 3.5

 

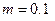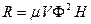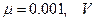Пластина массы кг, подвешенная на пружине, движется между полюсами магнита (Рис. 3.5). Вследствие вихревых токов движение тормозится силой, пропорциональной скорости. Сила сопротивления движению равна , где  – скорость в м/с,  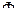– магнитный поток между полюсами магнита. В начальный момент скорость пластины равна нулю и пружина не растянута. Для удлинения пружины на 1 м необходимо приложить силу 19.6 Н. Определить движение пластины в том случае, когда 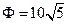Вб (Вебер – единица магнитного потока в СИ).

Дифференциальное уравнение движения пластины имеет вид:

 

                                           

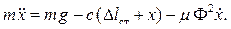
Учитывая условие статического равновесия

 

                                                             

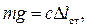
получаем:

                                                        

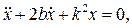
где

 

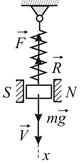
Рис. 3.5

                                                   

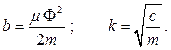
Вид решения зависит от соотношения между 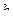 и 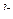. В рассматриваемом случае 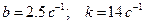. Таким образам,  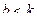и, следовательно, решение имеет вид:

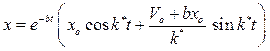                 , где

 

В начальный момент пластина покоится 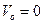 и пружина по условию не растянута; начало отсчета находится в положении статического равновесия. Учитывая условие статического равновесия, получаем:

                                               

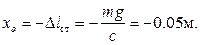
Окончательно получаем:

                                            

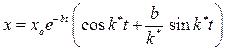
или, учитывая, что 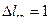м,  а 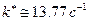, получаем:

 

                              

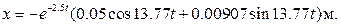
Пример 3.6

Определить движение пластинки при условиях предыдущей задачи (Рис. 3.5) в том случае, когда магнитный поток 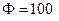Вб.

При таких условиях 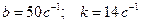 и, следовательно, имеет место случай большого сопротивления:

                                                   

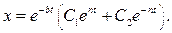
Скорость пластины определяется по формуле:

 

                                        

 

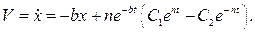
Для начального момента времени 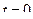 имеем

 

                                                    

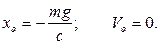
Следовательно,

                                      

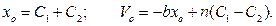
Отсюда:

                                     

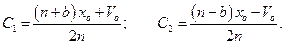
Учитывая, что начальная скорость равна нулю, получаем:

                                          

 

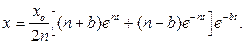
Остается добавить, что 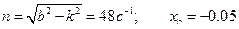м.

 

 

Пример 3.7

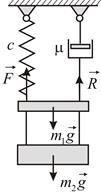
Грузы массы 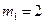кг и 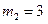кг подвешены в положении статического равновесия к пружине, коэффициент жесткости которой 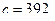Н/м (Рис. 3.6). Масляный демпфер вызывает силу сопротивления, пропорциональную первой степени скорости и равную  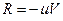где 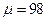Нс/м Груз  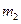сняли. Найти уравнение движения груза .

 

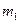Рис. 3.6

Совместим начало отсчета координаты  с положением статического равновесия груза 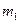. Дифференциальное уравнение движения груза  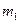имеет вид:

                                             

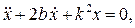
где

                      

 

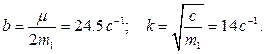
Таким образом, имеем дело со случаем большого сопротивления. Так же, как в примере 3.6 начальная скорость равна нулю. Аналогично получаем:

,

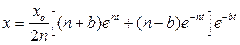причем .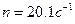

Остается определить 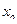. Пока груз  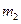не снят, он смещает груз  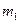из его положения равновесия, принятого за начало отсчета, в положительном направлении на величину

 

                                                            

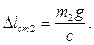
Это и есть начальная координата груза :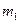

 

                                                       

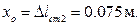
Окончательно получаем:

 

                                                                   

 

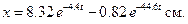
Пример 3.8

Найти уравнение движения точки массы 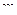, на которую действуют восстанавливающая сила  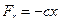и сила 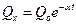, если в начальный момент точка находилась в положении равновесия в состоянии покоя.

 

Дифференциальное уравнение движения точки имеет вид:

 

                                                        

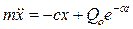
или

                                                          

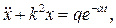
где

                                                      

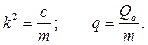
Частное решение будем искать в ви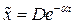де:

 

                                   ,   где 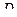– искомая константа.

 

Подставляя предполагаемый вид решения в уравнение, получаем:

 

                                                  

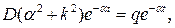
откуда

                                                            

 

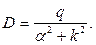
Получаем общее решение дифференциального уравнения движения в виде:

 

                                         

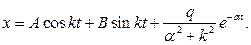
Вычислим скорость точки:

                                 

 

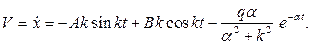
Остается определить постоянные интегрирования 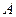 и 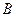. Подставляя начальные условия

 

                                              

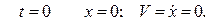
в полученные уравнения, находим:

 

                                              

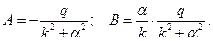
Окончательно получаем:

                                        

 

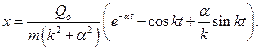
Пример 3.9

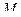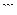Определить движение гири  массы , подвешенной на пружине 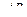, верхний конец которой начинает совершать гармонические колебания по вертикали амплитуды  с частотой 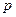 (Рис. 3.7). Жесткость пружины равна 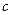. В начальный момент точка  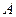занимает свое среднее положение и её скорость направлена вниз, а гиря  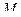висит на пружине в состоянии покоя.

Начальное положение точки 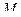, т.е. её положение статического равновесия, примем за начало координат, а ось  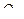направим по вертикали вниз.

Удлинение пружины в любой момент времени складывается из статического удлинения, удлинения, которое возникает при смещении груза из положения равновесия, при заданных начальных условиях, и удлинения за счёт принудительного перемещения верхнего конца пружины:

 

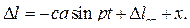
Возмущающая сила возникает из-за принудительного перемещения верхнего конца пружины:

 

 

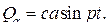
Дифференциальное уравнение движения имеет вид:

 

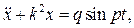
где

 

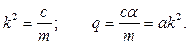
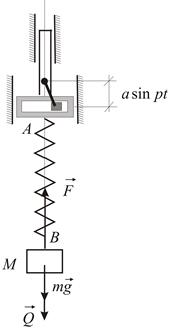
Рис. 3.7

Рассмотрим возможные случаи.

 

Если 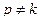, общее решение имеет вид:

 

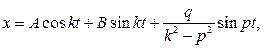
а скорость точки вычисляется по формуле:

 

 

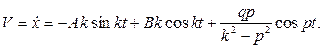
Подставляя в полученное общее решение нулевые (по условию задачи) начальные условия, находим:

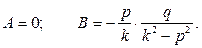
Искомое решение имеет вид:

 

                      

 

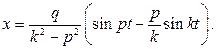
2. Если 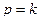, общее решение может быть записано в виде:

                                           

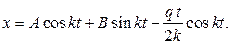
Для скорости точки получаем:

                               

 

Подставляя в полученное общее решение нулевые начальные условия, находим: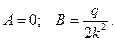

Окончательно получаем:

                              

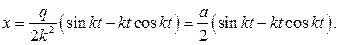
Пример 3.10

Статический прогиб рессор груженого товарного вагона 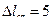см. Определить критическую скорость движения вагона, при которой начинается "галопирование" вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания вагона на рессорах; длина рельсов 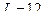м.

 

Очевидно, речь идет о резонансе, который наступит при совпадении частот собственных и вынужденных колебаний вагона. Определим частоту и период собственных колебаний:

 

                                      

 

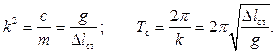
Период вынужденных колебаний равен времени прохождения вагоном одного рельса:

 

                                                                 

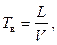
где 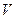 — скорость вагона.  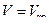при 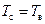, т.е.

 

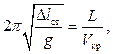                         отсюда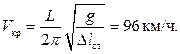  

 

 

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

 

Из сборника задач И.В.Мещерского: 32.1;  32.2; 32.4; 32.10; 32.16; 32.24; 32.28; 32.53; 32.54; 32.55; 32.78; 32.80; 32.84; 32.86; 33.6; 33.9; 33.10.

 

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-27; СР-28.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

---

Дата добавления: 2019-09-02; просмотров: 214; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!