Принцип возможных перемещений
Принцип возможных перемещений устанавливает условия равновесия механических систем. Под равновесием механической системы традиционно понимают состояние ее покоя по отношению к выбранной инерциальной системе отсчета.
Рассмотрим механическую систему, состоящую из 
материальных точек. Для ее равновесия необходимо и достаточно, чтобы суммы всех сил, действующих на каждую точку системы, и скорости всех точек в начальный момент времени равнялись нулю:
(7.1)
где 
– равнодействующая всех активных сил, действующих на точку с номером 
;
– равнодействующая всех сил реакций связей, наложенных на точку с номером 
.
Для равновесия механической системы с идеальными удерживающими стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к системе активных сил на любом возможном перемещении системы равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю:
(7.2)
Сформулированное утверждение называют принципом возможных перемещений. Необходимость. Пусть механическая система находится в равновесии. Следовательно, выполняются условия (7.1). Из данного положения дадим системе возможное перемещение. Умножим каждое из уравнений (7.1) скалярно на соответствующее точке возможное перемещение 
и сложим все полученные уравнения:
|
|
|
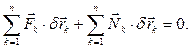(7.3)
По условию связи идеальные, следовательно, справедливо равенство (6.7). Из (6.7) и (7.3) получаем (7.2).
Достаточность. Приложим к точкам покоящейся механической системы систему сил, удовлетворяющих равенству (7.2) и, следовательно, поскольку связи идеальные (6.7), равенству
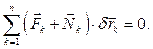(7.4)
Покажем, что механическая система останется в покое. Допустим противное – система под действием приложенных сил пришла в движение, т.е. ее точки получили ускорения 
. Эти ускорения должны быть направлены по касательным к траекториям точек, поскольку скорости равны нулю и нормальные составляющие ускорений отсутствуют. Таким образом, действительные перемещения точек пропорциональны их ускорениям. По условию связи стационарные и, следовательно, среди возможных перемещений системы найдется такое, которое совпадает с действительным. Возьмем в качестве возможного перемещения систему векторов, пропорциональных ускорениям точек 
. Равенство (7.4) примет вид: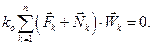 
или, учитывая, что для каждой точки справедлив второй закон Ньютона, 
|
|
|
Это равенство может иметь место только в том случае, если ускорения всех точек равны нулю 
Следовательно, механическая система после приложения активных сил останется в покое.
Заметим, что если вместо возможных перемещений использовать пропорциональные им возможные скорости (что позволяет в полной мере использовать при решении задач кинематические методы), то условия равновесия записываются в виде:
(7.5)
т.е.
для равновесия механической системы с идеальными, удерживающими, стационарными связями необходимо и достаточно, чтобы сумма мощностей всех приложенных к системе активных сил при любых возможных скоростях ее точек равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю.
Пример 1
Определить зависимость между модулями сил 
и 
в клиновом прессе, если сила приложена к концу рукоятки длины 
перпендикулярно плоскости, содержащей рукоятку и ось винта (Рис.7.8). Шаг винта равен 
. Угол при вершине клина 
.
Дадим системе возможное перемещение: пусть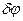 
– угол поворота рукоятки; 
– перемещение точки 
; 
– горизонтальное перемещение клина; 
– вертикальное перемещение точки 
.
|
|
|
|
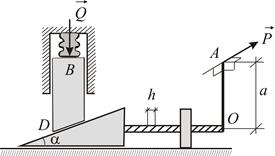
| Рис.7.8 |
При исследовании условий равновесия механизмов в зависимости от конкретной задачи, исходя из соображений удобства, можно использовать как возможные скорости, так и возможные перемещения. Для сравнения в этом первом разбираемом примере рассмотрим и возможные перемещения, и возможные скорости.
Условия равновесия системы можно записать в виде (7.2):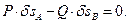 
Возможные перемещения связаны между собой соотношениями
. Отсюда: 
Теперь условия равновесия записываются в виде: 
Отсюда: 
Пример 2
Полиспаст состоит из неподвижного блока и 
подвижных блоков (Рис.7.9). Определить в случае равновесия отношение веса 
поднимаемого груза к величине силы 
, приложенной к свободному концу троса.
|
| Рис.7.9 |
Условие равновесия (7.5) имеет вид 
Рассмотрим первый из подвижных блоков. Точка 
– мгновенный центр скоростей блока. Возможная скорость точки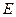 
численно равна возможной скорости точки 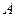. Следовательно, 
Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом, 
|
|
|
Подставляя полученный результат в условие равновесия, имеем:
Общее уравнение динамики
Рассмотрим механическую систему, состоящую из 
материальных точек, на которую наложены идеальные удерживающие связи. Уравнения движения точек имеют вид:
где
– равнодействующая всех активных сил, действующих на точку с номером ;
– равнодействующая реакций связей, наложенных на точку с номером .
При фиксированном времени дадим точкам системы возможные перемещения. Умножим каждое из уравнений движения скалярно на соответствующее возможное перемещение и сложим все полученные уравнения:
Поскольку по условию связи идеальные (6.7), последняя сумма равна нулю и, следовательно,
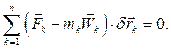(7.6)
Уравнение (7.6) называется общим уравнением динамики.
При использовании общего уравнения динамики удобно вводить в рассмотрение силы инерции. В этом случае уравнение (7.6) принимает вид:
(7.7)
Равенство (7.7) составляет содержание так называемого принципа Лагранжа–Даламбера:
в каждый момент времени для механической системы с идеальными удерживающими связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении системы равна нулю.
Пример
Призма массы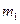 
может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки. Конец троса прикреплен к оси катка, который катится без скольжения по боковой поверхности призмы. Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы 
и одинакового радиуса 
. К барабану лебедки приложен постоянный вращающий момент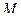 
. Составить дифференциальные уравнения движения системы.
Силовая и кинематическая схемы представлены на Рис.7.10. Общее уравнение динамики в рассматриваемом случае имеет вид:
|
| Рис.7.10 |
Система имеет две степени свободы. В качестве независимых координат примем координату призмы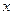 
и относительную координату оси катка 
. Кинематические условия, налагаемые связями, имеют вид: 
Отсюда: 
и 
Учитывая, что
получаем общее уравнение динамики в виде:
Поскольку возможные перемещения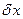 
и 
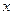могут принимать любые значения и не зависят друг от друга, общее уравнение динамики распадается на систему двух дифференциальных уравнений относительно координат и 
:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- В чём состоит принцип возможных перемещений?
- Как выглядит общее уравнение динамики?
ЛЕКЦИЯ 8 (16)
Дата добавления: 2019-09-02; просмотров: 302; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!