ПЕРВАЯ И ВТОРАЯ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Пример 1.1
Груз 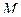 массы
массы  , подвешенный на нити длины
, подвешенный на нити длины 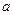 , другой конец которой закреплен в точке
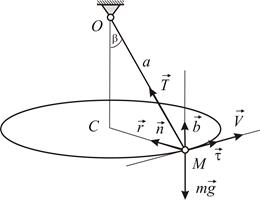
, другой конец которой закреплен в точке 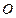 , представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости (Рис.1.1). Нить образует с вертикалью угол
, представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости (Рис.1.1). Нить образует с вертикалью угол 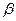 . Определить скорость груза
. Определить скорость груза 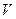 и силу натяжения нити
и силу натяжения нити 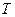 .
.
|
| Рис.1.1 |
Рассмотрим движение груза 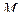 , который по условию задачи можно считать материальной точкой. Поскольку траектория точки известна, используем уравнения движения в проекциях на оси естественного трёхгранника. В рассматриваемом случае эти уравнения имеют вид:
, который по условию задачи можно считать материальной точкой. Поскольку траектория точки известна, используем уравнения движения в проекциях на оси естественного трёхгранника. В рассматриваемом случае эти уравнения имеют вид:
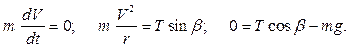
Последнее уравнение позволяет определить силу 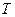 :
: 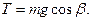 Из первого уравнения можно сделать вывод, что в процессе движения скорость точки не изменяет свою величину; определить эту величину можно из второго уравнения:
Из первого уравнения можно сделать вывод, что в процессе движения скорость точки не изменяет свою величину; определить эту величину можно из второго уравнения:
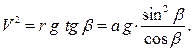
Заметим, что в решении фигурирует сила реакции нити, но искомая сила натяжения нити равна ей по модулю.
Пример 1.2
Автомобиль массы 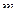 движется по выпуклому мосту равномерно со скоростью
движется по выпуклому мосту равномерно со скоростью 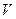 (Рис.1.2). Радиус кривизны в середине моста
(Рис.1.2). Радиус кривизны в середине моста 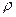 . Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
. Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
|
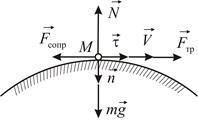
| Рис.1.2 |
Рассмотрим автомобиль в верней точке моста. Силы, действующие в направлении касательной к траектории – сила трения, сила сопротивления воздуха неизвестны. В направлении главной нормали к траектории действуют известная сила тяжести и нормальная реакция опоры, которую и требуется определить. Поэтому запишем уравнение движения в проекциях на главную нормаль к траектории. В рассматриваемом случае это уравнение принимает вид:
|
|
|
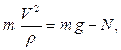 отсюда:
отсюда: 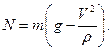
По третьему закону Ньютона сила давления автомобиля на мост по модулю равна нормальной реакции.
Пример 1.3
Решето рудообогатительного грохота движется поступательно по вертикали по закону 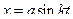 . Найти наименьшую частоту
. Найти наименьшую частоту 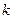 колебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.
колебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.
|
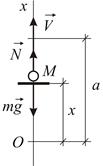
| Рис.1.3. |
Направим ось 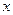 вертикально вверх (Рис.1.3). Дифференциальное уравнение движения имеет вид:
вертикально вверх (Рис.1.3). Дифференциальное уравнение движения имеет вид:
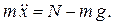
Отсюда:
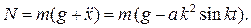
Минимальное значение нормальная реакция принимает в верхней точке, где 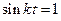 :
:
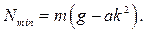
Если кусок руды отделяется от решета, то 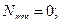 отсюда
отсюда
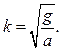
|
|
|
Пример 1.4
Материальная точка массы 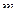 совершает прямолинейное движение под действием силы, изменяющейся по закону
совершает прямолинейное движение под действием силы, изменяющейся по закону 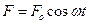 , где
, где 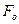 и
и 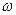 — постоянные величины. В начальный момент точка имела скорость
— постоянные величины. В начальный момент точка имела скорость 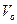 . Найти уравнение движения точки.
. Найти уравнение движения точки.
Направим ось 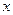 вдоль прямой, по которой движется точка, совместив начало отсчета с начальным положением точки. На основании второго закона Ньютона в проекции на ось
вдоль прямой, по которой движется точка, совместив начало отсчета с начальным положением точки. На основании второго закона Ньютона в проекции на ось 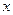 получаем:
получаем:
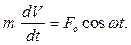
Интегрируя полученное дифференциальное уравнение движения точки
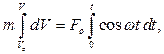
определяем зависимость ее скорости от времени: 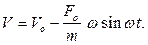
Поскольку 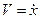 , полученное уравнение представляет собой дифференциальное уравнение относительно функции
, полученное уравнение представляет собой дифференциальное уравнение относительно функции 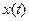 :
:
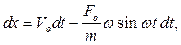
интегрируя которое, определяем закон движения точки:
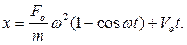
Пример 1.5
На какую высоту 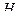 и за какое время
и за какое время 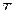 поднимется тело весом
поднимется тело весом 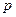 , брошенное вертикально вверх со скоростью
, брошенное вертикально вверх со скоростью 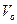 , если сопротивление воздуха может быть выражено формулой
, если сопротивление воздуха может быть выражено формулой 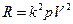 , где
, где 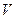 — скорость тела?
— скорость тела?
|
|
|
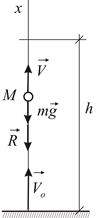
Направим ось 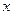 вертикально вверх, полагая
вертикально вверх, полагая 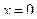 на поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:
на поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:
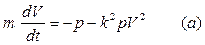
или, учитывая что 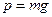 , вид:
, вид:
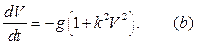
|
| Рис.1.4 |
Уравнение 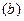 представляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:
представляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:
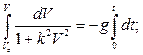
отсюда:
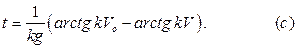
Теперь мы имеем возможность определить время подъема тела на максимальную высоту. Подставляя в уравнение (с) условия
при  получаем
получаем 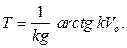
Остается определить максимальную высоту подъема 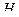 . Уравнение
. Уравнение 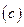 можно рассматривать как дифференциальное уравнение относительно функции
можно рассматривать как дифференциальное уравнение относительно функции 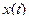 , поскольку
, поскольку 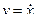 , но интегрирование уравнения
, но интегрирование уравнения
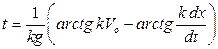
представляется неудобным.
Помимо зависимости 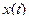 , для определения
, для определения 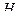 нас вполне устраивает зависимость
нас вполне устраивает зависимость 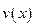 , поскольку скорость в верхней точке известна:
, поскольку скорость в верхней точке известна: 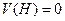 . Перейдем в уравнении
. Перейдем в уравнении 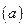 от производной по
от производной по 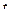 к производной по
к производной по 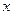 , полагая
, полагая
|
|
|
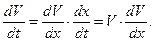
Уравнение 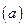 принимает вид:
принимает вид:
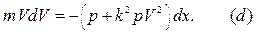
Интегрируя уравнение 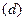
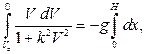 получаем:
получаем: 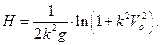
Заметим, что соотношение  представляет собой одну из форм записи теоремы об изменении кинетической энергии, которую мы докажем позднее.
представляет собой одну из форм записи теоремы об изменении кинетической энергии, которую мы докажем позднее.
Дата добавления: 2019-09-02; просмотров: 197; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
