Примеры динамического исследования сложных систем
При изучении движения механической системы, как правило, необходимо использовать несколько теорем. Если система состоит из нескольких твердых тел, то в большинстве случаев оказывается удобным (а иногда необходимым) разделить систему на части, рассматривая движение каждого тела, входящего в систему, в отдельности.
Пример 4.15
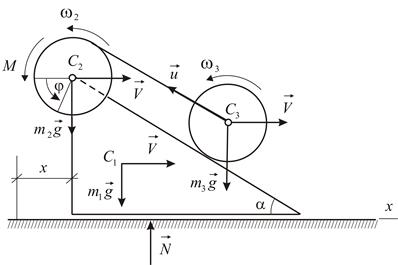
Призма (тело 1) массы 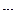 может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки (тело 2). Конец троса прикреплен к оси катка (тело 3), который катится без проскальзывания по боковой поверхности призмы (Рис. 4.15). Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы
может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки (тело 2). Конец троса прикреплен к оси катка (тело 3), который катится без проскальзывания по боковой поверхности призмы (Рис. 4.15). Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы 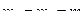 и одинакового радиуса
и одинакового радиуса 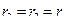 . К барабану лебедки приложен постоянный вращающий момент
. К барабану лебедки приложен постоянный вращающий момент 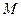 . Определить движение системы, если в начальный момент времени она находилась в покое.
. Определить движение системы, если в начальный момент времени она находилась в покое.
Система имеет две степени свободы. В качестве параметров, определяющих положение системы примем координату 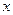 призмы и угол поворота
призмы и угол поворота 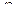 барабана лебедки.
барабана лебедки.
|
| Рис. 4.15 |
Заметим, что внешние силы, приложенные к системе в целом, не имеют проекций на направление движения призмы (Рис. 4.15). Записывая теорему об изменении количества движения механической системы в проекциях на координатную ось 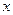 ,
,
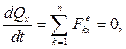
получаем:
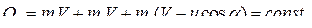
|
|
|
где 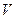 – скорость призмы, а
– скорость призмы, а 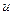 – относительная скорость оси катка. Учитывая, что в начальный момент система находилась в покое,
– относительная скорость оси катка. Учитывая, что в начальный момент система находилась в покое, 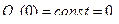 получаем:
получаем:
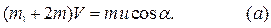
| 
| |
| Рис. 4.16 | Рис. 4.17 |
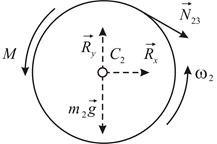
Дифференциальное уравнение вращательного движения для барабана лебедки имеет вид (Рис. 4.16):
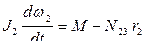
или, учитывая, что  и
и 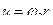
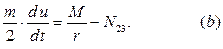
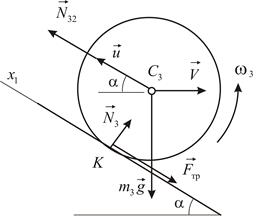
Для катка запишем теорему о движении центра масс в проекциях на направление оси 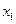 (вдоль наклонной плоскости) и дифференциальное уравнение вращения (Рис. 4.17):
(вдоль наклонной плоскости) и дифференциальное уравнение вращения (Рис. 4.17):
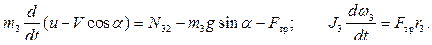
Точка 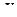 является мгновенным центром скоростей катка в его относительном движении. Учитывая, что
является мгновенным центром скоростей катка в его относительном движении. Учитывая, что 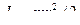 и
и 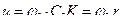 , получаем:
, получаем:
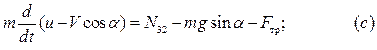
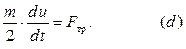
Исключая из системы уравнений 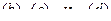 , силы
, силы 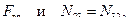 получаем:
получаем:
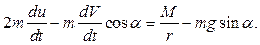
Это уравнение после интегрирования при нулевых начальных условиях принимает вид:
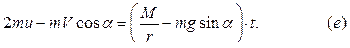
|
|
|
Задача свелась к решению системы уравнений 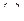 и
и 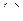 . Получаем:
. Получаем:
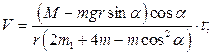
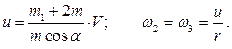
Пример 4.16
Каток массы  радиуса
радиуса 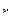 катится без скольжения по горизонтальной поверхности под действием приложенного к нему постоянного вращающего момента
катится без скольжения по горизонтальной поверхности под действием приложенного к нему постоянного вращающего момента 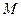 . Трос, намотанный на боковую поверхность катка, сходит с него горизонтально и попадает на неподвижный блок массы
. Трос, намотанный на боковую поверхность катка, сходит с него горизонтально и попадает на неподвижный блок массы 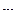 и радиуса
и радиуса 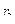 (Рис.4.18). К свободному концу троса привязан груз массы
(Рис.4.18). К свободному концу троса привязан груз массы  . Считая каток и блок сплошными однородными цилиндрами определить скорость оси катка
. Считая каток и блок сплошными однородными цилиндрами определить скорость оси катка 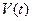 . если в начальный момент времени система находилась в покое.
. если в начальный момент времени система находилась в покое.
Рассматривая движение каждого из тел системы в отдельности, записываем: теорему о движении центра масс катка в проекциях на горизонтальное направление:
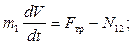
дифференциальное уравнение вращательного движения катка:
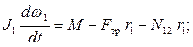
дифференциальное уравнение вращательного движения блока:
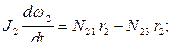
|
| Рис. 4.18 |
и теорему о движении центра масс груза в проекциях на вертикальное направление:
|
|
|
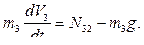
Учитывая очевидные кинематические соотношения:
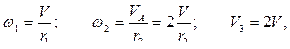
а также тот факт, что
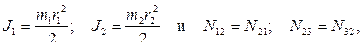
получаем дифференциальное уравнение:
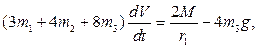
интегрируя которое при нулевых начальных условиях, находим:
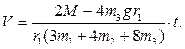
Пример 4.17
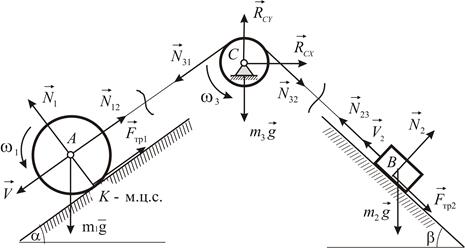
Колесо 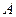 скатывается без скольжения по наклонной плоскости, образующей угол
скатывается без скольжения по наклонной плоскости, образующей угол 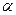 с горизонтом (Рис. 4.19). К оси колеса привязан трос, переброшенный через неподвижный блок
с горизонтом (Рис. 4.19). К оси колеса привязан трос, переброшенный через неподвижный блок 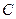 и прикрепленный к грузу
и прикрепленный к грузу 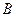 , поднимающемуся по наклонной плоскости, образующей угол
, поднимающемуся по наклонной плоскости, образующей угол 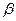 с горизонтом. В начальный момент система находилась в покое. Колесо и блок представляют собой сплошные однородные диски с массами
с горизонтом. В начальный момент система находилась в покое. Колесо и блок представляют собой сплошные однородные диски с массами  и
и  и радиусами
и радиусами 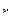 и
и 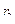 соответственно. Масса груза равна
соответственно. Масса груза равна 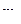 . Коэффициент трения между грузом и наклонной плоскостью равен
. Коэффициент трения между грузом и наклонной плоскостью равен 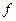 . Определить скорость оси колеса, натяжение троса на участках
. Определить скорость оси колеса, натяжение троса на участках 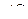 и
и 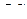 , реакцию оси блока
, реакцию оси блока 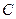 .
.
Рассмотрим движение каждого из трех тел в отдельности. Силовые схемы представлены на Рис. 4.19.
Колесо совершает плоско-параллельное движение. Одну из осей координат направим вниз по наклонной плоскости (в сторону движения центра колеса). Дифференциальные уравнения движения имеют вид:
|
|
|
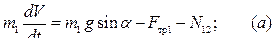
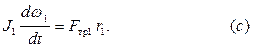
Груз  движется поступательно:
движется поступательно:
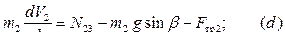
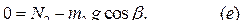
Тело 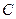 вращается вокруг неподвижной оси:
вращается вокруг неподвижной оси:
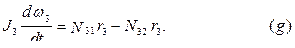
|
| Рис. 4.19 |
Приведенную систему уравнений необходимо дополнить кинематическими соотношениями:
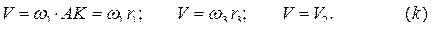
Поскольку масса троса не учитывается, то
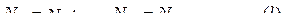
Сила трения скольжения между грузом и опорной поверхностью определяется по формуле:
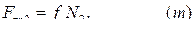
Для определения реакции оси блока 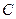 используем теорему о движении центра масс (применительно к блоку
используем теорему о движении центра масс (применительно к блоку 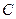 ):
):
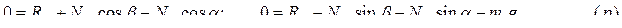

При решении полученной системы уравнений, прежде всего, необходимо определить скорость оси колеса. Используя уравнения 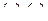 и первое из уравнений
и первое из уравнений 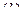 , получаем:
, получаем:
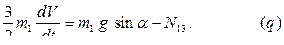
Используя уравнения  и третье из уравнений
и третье из уравнений 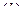 , получаем:
, получаем:
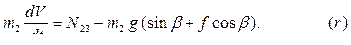
С учетом уравнений 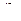 и второго уравнения
и второго уравнения 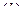 , из
, из 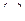 получаем:
получаем:
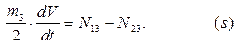
Складывая уравнения  , получаем:
, получаем:
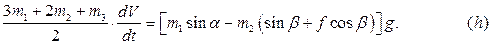
Из уравнения  находим ускорение центра
находим ускорение центра  колеса:
колеса:
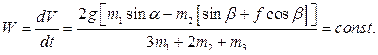
Интегрируя по времени при нулевых начальных условиях, определяем скорость центра 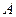 колеса:
колеса:
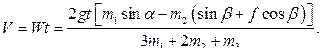
Подставляя ускорение 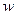 центра колеса в уравнения
центра колеса в уравнения 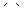 и
и 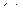 , определяем натяжение троса на участках
, определяем натяжение троса на участках 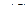 и
и 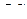 :
:
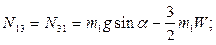
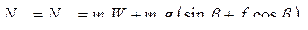
Из уравнений  определяем реакцию шарнира
определяем реакцию шарнира 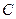 блока:
блока:
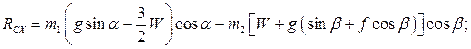
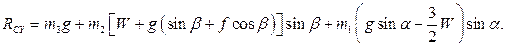
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 37.6; 37.9; 37.43; 37.44; 37.46; 37.50; 37.52; 37.56; 37.57; 37.58; 39.4; 39.6; 39.11; 39.13; 39.15; 39.19.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-30; СР-31.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5
Дата добавления: 2019-09-02; просмотров: 199; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
