Вычислим ошибку коэффициента регрессии

 

,                                 (2.17)

 

.

 

Вычислим остаточную сумму квадратов

 

.

 

Отсюда: .

 

В остальном методика проверки значимости отличия коэффициента регрессии от нуля аналогична проверке значимости коэффициента корреляции.

 

.                                                      (2.18)

 

Коэффициент регрессии показывает, насколько изменяется зависимая переменная при изменении независимой переменной на единицу.

Для данного случая табличное значение t-критерия при восьми степенях свободы и 95 % доверительности равно 2,106. Таким образом, t_b > t_таб, и, следовательно, коэффициент регрессии значимо отличен от нуля.

 

Рассчитаем коэффициент эластичности

 

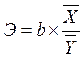,                                                   (2.19)

 

.

 

Коэффициент эластичности показывает, на сколько % увеличится Y при увеличении Х на 1 %.

 

Таблица 2.5 – Промежуточные результаты

Значение коэффициента а	Значение коэффициента b	Ошибка коэффициента регрессии, Sb	Коэффициент эластичности, Э
6,3	0,0217	0,0044	4,96

 

ВЫВОД: Таким образом, произведенный анализ показывает, что величина рентабельности предприятия связана с производительностью труда (коэффициент корреляции 0,78). Из полученного уравнения регрессии  следует, что увеличение производительности труда на 1 тыс. руб. приведет к повышению рентабельности на 0,0217 тыс. руб. Изменение производительности труда на 1 % приведет к увеличению рентабельности на 0,325 %.

 

II ЭТАП (решение задачи с помощью ТП MS Excel)

 

Решение задачи с помощью табличного процессора MS Excel представлено в приложениях 2 и 3.

ОПТИМИЗАЦИОННЫЕ МОДЕЛИ.

ЛИНЕЙНЕОЕ ПРОГРАММИРОВАНИЕ

 

Общая постановка задач линейного программирования

 

Линейноепрограммирование – это один из разделов математического программирования, изучающий способы поиска (отыскания) максимума или минимума линейной функции нескольких переменных при наличии линейных ограничений, т. е. линейных равенств или неравенств, связывающих эти переменные.

К задачам оптимального планирования относится достаточно широкий круг задач оптимизации.

Задача оптимизации – это задача выбора таких условий и зависящих от них факторов, при которых критерий эффективности достигает экстремального значения.

Под решениемзадачоптимизации понимается процесс выбора таких значений переменных х, принадлежащих допустимой области D, которые обеспечивают оптимальное значение некоторой функции F( x), называемойцелевой.

Если целевая функция линейна, а область допустимых значений задается системой линейных уравнений или неравенств, то такая задача являетсязадачейлинейногопрограммирования.

Модель задачи линейного программирования должна иметь вполне определенный вид: требуется найти максимум (минимум) значения целевой функции L при переменных x₁, x₂, _…, x_n.

Общая математическая формулировка задачи линейного программирования выглядит следующим образом:

 

,          (3.1)

 

при соблюдении линейных ограничений

 

                         (3.2)

 

Каждая  из переменных не может принимать отрицательного значения, т. е.

 

                                     (3.3)

 

В выражениях (3.1) и (3.2) коэффициенты a_ij и c_j при переменных и величины b_i – постоянныечисла.

Решение системы уравнений (3.2) при выполнении условия (3.3) называетсядопустимым решением задачи линейногопрограммирования.

Оптимальное решение – это допустимое решение, удовлетворяющее условию (3.1). Для нахождения оптимального решения следует иметь множество допустимых решений. Если число уравнений m в системе (3.2) равно числу переменных n, то такая система уравнений имеет только одно решение. В задачах линейного программирования число уравнений должно быть меньше числа переменных: m<n.

Все переменные, входящие в систему ограничений, должны быть и в целевой функции. Свободные члены b₁, b₂, _…, b_m в системе ограничений должны быть положительными или равны нулю (>=0).

Достаточно часто ограничения (3.2) задаются в виде системы неравенств.

Существует только одна переменная, и ищется только один экстремум.

Требуется найти такое неотрицательное решение системы (3.2), т. е.  (3.3), при котором функция L( x) достигает максимума или минимума.

Функция (3.1) – целевая функция; уравнение (3.2) – ограничения данной функции; неравенство (3.3) – условие не отрицательности.

В сокращенной записи задача линейного программирования заключается в минимизации (максимизации) функции

 

,                                     (3.4)

 

при условиях, что

 

                             (3.5)

 

и

 

.                                           (3.6)

 

К типовым оптимизационным задачам линейного программирования можно отнести:

§ оптимизация производственной программы;

§ оптимизация раскроя материалов;

§ оптимизация состава смеси;

§ оптимизация перевозок;

§ оптимизация финансовых показателей;

§ оптимизация штатного расписания и т. п.

 

---

Дата добавления: 2019-07-17; просмотров: 202; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!