Сущность двойственной экономико-математической задачи и двойственных оценок (0.0.0.).
Каждой задаче линейного программирования можно определенным образом сопоставить другую задачу , называемую двойственной или сопряженной по отношению к исходной .Oпределение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции 
(1)
при условиях
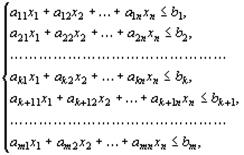(2)
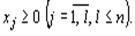(3)
Определение 1. Задача, состоящая в нахождении минимального значения функции
(4) при условиях
(5)
(6)
называется двойственной по отношению к задаче (1) – (3). Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:1. Целевая функция исходной задачи (1) – (3) задается на максимум, а целевая функция двойственной (4) – (6) – на минимум.2. Матрица
(7)
составленная из коэффициентов при неизвестных в системе ограничений (2) исходной задачи (1) – (3), и аналогичная матрица
(8)
в двойственной задаче (4) – (6) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками).
3. Число переменных в двойственной задаче (4) – (6) равно числу ограничений в системе (2) исходной задачи (1) – (3), а число ограничений в системе (5) двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (4) двойственной задачи (4) – (6) являются свободные члены в системе (2) исходной задачи (1) – (3), а правыми частями в соотношениях системы (5) двойственной задачи – коэффициенты при неизвестных в целевой функции (1) исходной задачи.
|
|
|
5. Если переменная xj исходной задачи (1) – (3) может принимать только лишь положительные значения, то j–е условие в системе (5) двойственной задачи (4) – (6) является неравенством вида “? ”.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (2) прямой задачи и соотношения (5) двойственной задачи являются неравенствами вида “ 
”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем в последней переменные могут быть и отрицательными. В симметричных задачах система ограничений как исходной, так и двойственной задачи задается неравенствами, причем на двойственные переменные налагается условие неотрицательности.
Конкретными экономическими свойствами оценок yi (двойственных оценок) оптимального плана является:
Свойство 1. Оценки как мера дефицитности ресурсов и продукции.
|
|
|
Свойство 2. Оценки как мера влияния ограничений на функционал.
Свойство 3. Оценки как инструмент определения эффективности отдельных вариантов.
Свойство 4. Оценки как инструмент балансирования суммарных затрат и результатов.
Экономическое истолкование оценок есть интерпретация их общих экономико-математических свойств применительно к конкретному содержанию задачи. Не использованный полностью в оптимальном плане ресурс получает нулевую оценку. Нулевая оценка ресурса свидетельствует о его недефицитности. Ресурс недефицитен не из-за его неограниченных запасов (они ограничены величиной bi), а из-за невозможности его полного использования в оптимальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производства им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию f().
Ограничивают целевую функцию дефицитные ресурсы. В рассматриваемой сельскохозяйственной задаче – пашня и механизированные работы. Они полностью использованы в оптимальном плане. Оценка таких ресурсов положительна (у1 =1; y3 =0,75). Трудовые ресурсы имеют нулевую оценку (у2=0), они недефицитны.
|
|
|
Оценка ресурса показывает, на сколько изменится критерий оптимальности при изменении количества данного ресурса на единицу. Для недефицитного ресурса оценка равна нулю, поэтому изменение его величины не повлияет на критерий оптимальности. Дефицитность ресурса измеряется вкладом единицы ресурса в изменение целевой функции.
Дата добавления: 2019-07-15; просмотров: 324; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!