Методы и методики сглаживания мультиколлинеарности. Каскадный анализ.

Если основная задача модели - прогноз будущих значений зави­симой переменной, то при достаточно большом коэффициенте детер­минации R² (≥0.9) наличие мультиколлинеарности зачастую не ска­зывается на прогнозных качествах модели. Хотя это утверждение бу­дет обоснованным лишь в том случае, что и в будущем между корре­лированными переменными будут сохраняться те же отношения, что и ранее.

Если же целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую перемен­ную, то наличие мультнколлннеарности, приводящее к увеличению стандартных ошибок, скорее всего, исказит истинные зависимости между переменными. В этой ситуации мультнколлинеарность пред­ставляется серьезной проблемой.

Исключение переменной(ых) из модели

Простейшим методом устранения мультиколлинеарности являет­ся исключение из модели одной или ряда коррелированных перемен­ных.

В этой ситуации возможны ошибки специфи­кации. Например, при исследовании спроса на некоторое благо н каче­ство объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррели­руют друг с другом. Исключив из модели цены заменителей, мы, ско­рее всего, допустим ошибку спецификации. Вследствие этого воз­можно получение смещенных оценок и осуществление необоснован­ных выводов. Таким образом, в прикладных эконометрических моде­лях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой.

2. Получение дополнительных данных или новой выборки

Т.к. мультиколлинеариость напрямую зависит от выборки, то, возможно, при другой выборке мультиколлинеарности не будет либо она не будет столь серьезной.

Иногда для уменьшения мультиколлинеарности достаточно уве­личить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Увеличение коли­чества данных сокращает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость. Однако получение новой выборки или расширение старой не всегда возможно или связа­но с серьезными издержками. Кроме того, данный подход может уси­лить автокорреляцию. Эти проблемы ограничивают возможное ис­пользования данного метода.

3. Изменение спецификации модели

 В ряде случаев проблема мультиколлинеарности может быть ре­шена изменением спецификации модели: либо изменением формы модели, либо добавлением объясняющих переменных, которые не уч­тены в первоначальной модели, но существенно влияющие на зависи­мую переменную. Если данный метод имеет основания, то его исполь­зование уменьшает сумму квадратов отклонений, тем самым сокращая стандартную ошибку регрессии. Это приводит к уменьшению стан­дартных ошибок коэффициентов.

Использование предварительной информации о некоторых параметрах

Иногда при построении модели множественной регрессии можно воспользоваться некоторой предварительной информацией, в часто­сти, извостными значениями некоторых коэффициентов регрессии. Вполне вероятно, что значения коэффициентов, полученные для каких-лнбо предварительных (обычно более простых) моделей, либо для аналогичной модели по ранее полученной выборке, могут быть ис­пользованы для разрабатываемой в данный момент модели.

Для иллюстрации приведем следующий пример. Строится ре­грессия вида (1).

Y = β₀+ β₁×X₁+ β₂×X₂+ε

 Предположим, что переменные X₁ и Х₂ коррели­рованны. Для построенной модели парной регрессии Y = γ₀+γ₁×X₁ + ν  

был определен статистически значимый коэффициент γ₁ (для определенности пусть γ₁= 0.8), связывающий Y с Х₁. Если есть осно­вания думать, что связь между Y и Х₁ останется неизменной, то мож­но положить, что γ₁= β₁=0.8. Тогда (1) примет вид:

Y = β₀+ 0.8×X₁+ β₂×X₂+ε => Y- 0.8X₁ = β₀+ β₂×X₂+ε   (2)

Уравнение (2) фактически является уравнением парной ре­грессии, для которого проблема мультиколлинеарности не существу­ет.

Ограниченность использования данного метода обусловлена тем, что:

1) получение предварительной информации зачастую за­труднительно;

2)вероятность того, что выделенный коэф­фициент регрессии будет одним и тем же для различных моделей, не­высока.

Преобразование переменных

В ряде случаев минимизировать либо вообще устранить пробле­му мультиколлинеарности можно с помощью преобразования пере­менных.

Например, пусть эмпирическое уравнение регрессии имеет вид

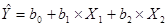                                                    (3)

причем X₁ и Х₂ - коррелированные переменные. В этой ситуации можно попытаться определять регрессионные зависимости относи­тельных величин

 

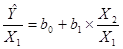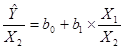,   (4)

 

Вполне вероятно, что в моделях, аналогичных (4), проблема мультиколлинеариости будет отсутствовать.

Возможны п другие преобразования, близкие по своей сути к вышеописанным. Например, если в уравнении рассматриваются взаи­мосвязи номинальных экономических показателей, то для снижения мультиколлинеариости можно попытаться перейти к реальным пока­зателям и т. д.

 

---

Дата добавления: 2019-07-15; просмотров: 270; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!