Основные характеристики соответствия данных требованиям закона нормального распределения (ЗНР).
ЗНР (или закон Гаусса) характеризуется тем, что выбор однородно сформирован по одинаковым закономерностям, то вероятность появления значения возрастает по мере приближения их величины к средней арифметической.
Функция плотности вероятности ЗНР определяется формулой:
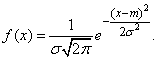(1.1)
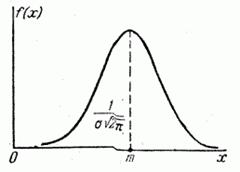
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 1.1). Максимальная ордината кривой, равная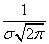 
, соответствует точке 
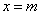; по мере удаления от точки 
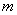плотность распределения падает, и при 
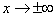кривая асимптотически приближается к оси абсцисс.
Основными характеристиками соответствия данных требованиям ЗНР является: - ассиметрия (А)
; 
, 
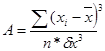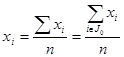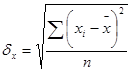
где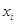 
- значение проверяемого столбца и фактора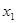 
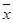- среднее арифметическое значение;
n – число объектов (20 и более)
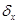- стандартная ошибка
- эксцес (Э)
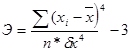
Если информация идеально и отвечает ЗНР, то А, Э = 0; а если информация неоднородна, то А, Э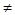 
0.
, 
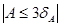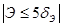- знак всегда положителен и отвечает ЗНР;
, 
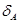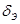= f (n), вытекает из закона больших чисел (100 и более) и зависит от значения данных.
Нарушение указанных требований, а именно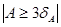 
, 
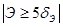, среди проверяемых данных, и есть сильно выделяющие значения.
Сущность закона «трех сигм» и его экономическое содержание.
При рассмотрении ЗНР выделяется важный частный случай, известный как правило «трех сигм». Смысл, которого заключается в определении, принадлежат ли те или иные значения проверяемому столбцу.
|
|
|
Значение принадлежит проверяемому столбцу, если вероятность попадания в интервал (а – 3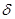 
; а + 3 
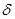), то есть вероятность того, что 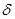принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.
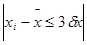- это правило «трех сигм».
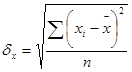
На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Таким образом, при поверке на достоверность всех столбцов, исключаем ≈ 20-25 % объектов, отсюда следует, что min число объектов на основе, которых рассчитывается эконометрическая модель, было < 20, а на начальной стадии надо брать на 20-25 % больше (т.е. 24-25 штук).
Методы и методики обоснования вида ЭМ.
Экспертные оценки обоснования значимости качественных признаков-факторов ЭМ.
В обосновании информации существенное место принадлежит экспертным оценкам. Ценность этих особенно возрастает в период преобразований, перехода от одной формы хозяйствования к другим. Поэтому в нынешних условиях при обосновании программ развития было бы правильно начинать обоснование программ с экспертных оценок. Они должны дать ответ на вопрос: в каком направлении осуществлять развитие, т.е. экспертные оценки позволяют обосновать стратегию развития.
|
|
|
В использовании экспертных оценок существует два подхода:
1. Оценка тенденции, направления развития осуществляется по совокупности факторов одной количественной величиной, чаще всего по 5-тибальной системе. Если по сумме баллов рассматривая концепция имеет 4,5-5 баллов - концепция принимается как единственная и доминирующая; 3,5-4,5 – концепция преобладающая, однако есть параллельные, на которые надо обратить внимание и быть готовыми к их рассмотрению; 2,5-3,5 – есть альтернативные концепции, заслуживающие внимания, которые должны получить развитие.
2. Использование экспертных оценок основано на том, что крупная концепция расчленяется на элементы и оценка важности отдельных элементов позволяет, во-первых, установить приоритет, т.е. очередность решения составляющих проблемы; во-вторых, дать положительную или отрицательную оценку проблемы в целом.
Методика предполагает ранжирование элементов проблемы. Число рангов зависит от числа показателей. Если проблема включает 5 элементов, то самый важный элемент, по мнению эксперта, получает ранг или балл 5 и так да до 1. С помощью специальных формул рассчитывается коэффициент согласованности оценок экспертов. Если выясняется, что он высок, т.е. отвечает критерию проверки, то проблема решается в очередности, вытекающей из суммы рангов по определенным элементам проблемы.
|
|
|
Допустим, что n – число элементов или признаков проблемы; n(n – 1)/2 – сумма рангов или оценок эксперта. Каждый элемент проблемы или признак будет иметь число рангов, которое определяется по формуле:
T = N *(n+1/2), где N – число экспертов.
По каждому элементу проблемы рассчитываем величину отклонения суммы рангов от средней величины.
Решение ЭМ задачи связано с поиском варианта, отвечающего многим требованиям, которые с одной стороны выражаются ограничениями задачи, а с другой записываются требованиями к решению, которые выражаются через критерий оптимальности. Критерий оптимальности есть качественная категория, выражающая требования общества в целом и коллектива, применительно к условиям которого решается задача, к уровню эффективности использования ресурсов.
В силу ограниченности ресурсов надо найти такое решение, учитывающее несколько требований, необходим поиск компромиссного решения.
|
|
|
Наиболее известные методы экспертных оценок: метод Дельфи, мозговой штурм и метод анализа иерархий. Каждому методу соответствуют свои сроки проведения и потребность в экспертах. После выбора метода экспертного оценивания можно определить затраты на процедуру, которые включают оплату экспертов, аренду помещения, приобретение канцтоваров, оплату специалиста по проведению и анализу результатов экспертизы.
Дата добавления: 2019-07-15; просмотров: 363; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!