Построение уравнения регрессии по результатам ПФП

С параллельными опытами

Def . Пусть W_х – область возможных значений входных параметров объекта, которую назовем областью планирования. Планом эксперимента называется некоторое подмножество Р(W_х) Ì W_х точек, в которых проводятся эксперименты. Обычно план задается матрицей значений входных параметров в экспериментальных точках Х=[ 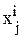] – матрицей планирования, i =1,…N, j = 1,…, m.

Рассмотрим типичный случай, когда областью значений входных параметров объекта является гиперкуб: W_х = [ –1, +1] ^m, т.е. 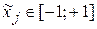, j = 1,…m. Для произвольного отрезка [ 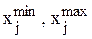] легко найти замену переменных, переводящую его в [ –1, +1]:

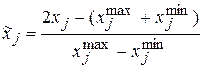,                               (3.11)

где 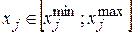 – размерные (натуральные) переменные,  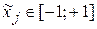– безразмерные переменные.

Одним из наиболее популярных планов экспериментов является полный факторный план (ПФП) – это план, в котором каждый входной параметр принимает только два значения: +1 и –1 и при этом перебираются все возможные комбинации. Число строк в матрице Х равно N =2^m.

Основное свойство ПФП: столбцы матрицы Ф, заданные в безразмерных переменных для линейной

y = b₀ + b₁x₁ +…+ b_mx_m

и неполной квадратичной

y = b₀ + b₁x₁ +…+ b_mx_m + b₁₂ x₁ x₂ + b₁₃ x₁ x₃ + … + b_{m –1, m} x_{m –1} x_m

моделей в ПФП ортогональны, а, следовательно, матрица Ф^ТФ диагональна и равна N×I_k.

Благодаря этому свойству

- МНК-оценки коэффициентов модели независимы;

- матрица Ф^ТФ имеет наилучшую обусловленность.

Пример 3.1. Пусть даны матриц ПФП для m = 3 в безразмерных (X1) и размерных (X2) переменных (W_х = [0; 2] ´ [15; 20] ´ [6; 8]):

 

;                  .

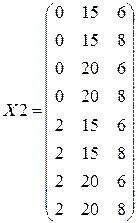Пусть имеем результаты экспериментов, согласно плану с матрицей Х2 и четырьмя параллельными опытами. Результаты опытов – в матрице Y:

 

 

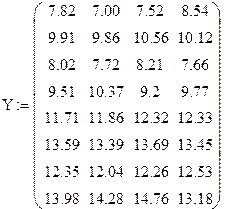
В каждой экспериментальной точке найдем среднее значение выхода 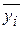 по параллельным опытам (среднее по каждой строке матрицы Y):

 

 

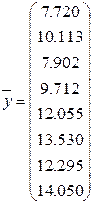
Для проверки гипотезы об однородности точечных дисперсий вычислим значение критерия Кочрена: 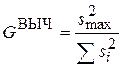  = 0,308,  где вектор точечных дисперсий  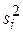имеет вид:

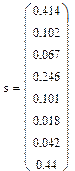
а 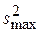= 0.440. По таблице ПРИЛОЖЕНИЯ 2 находим G^ТАБЛ (0.05, 8, 3) = 0.4377. Следовательно, гипотеза об однородности дисперсий принимается.

Пусть требуется построить линейную модель Y = b₀ + b₁ x₁ + b₂ x₂ + b₃ x₃.

Поскольку все ценные качества ПФП проявляются при использовании безразмерных переменных, то построим модель в безразмерных переменных 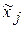, значения которых указаны в матрице Х1.

Вычислим элементы регрессионной матрицы:

.

Далее с помощью функции lsolve решим линейную систему уравнений

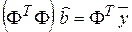
и найдём вектор МНК-оценок регрессии в безразмерных переменных:

.

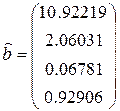Проведём анализ полученного уравнения.

1) По формулам (3.5), (3.6) найдём дисперсию воспроизводимости 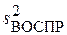 = 0.1786.

2) По формуле (3.10) найдём значения критерия Сьюдента для МНК-оценок

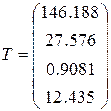
при Т^КРИТ = qt(0,975, 8×3) = 2.064. Оценка 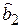 незначима. Исключим её.

Повторим все вычисления при исключённом столбце матрицы Х1, соответствующим 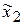. Получим следующие результаты.

Вектор МНК-оценок регрессии в безразмерных переменных:

.

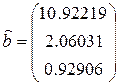Как видим, после пересчёта с новой матрицей Ф значения оставшихся оценок не изменились. Это связано с ортогональностью ПФП.

Поскольку дисперсия воспроизводимости не зависит от построенной модели, её значение не изменилось. Остались неизменными и значения критерия Стьдента у оставшихся МНК-оценок 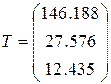 а Т^КРИТ = qt(0,975, 8×3) = 2.064. Все МНК-оценки значимы.

1) Исследуем эффективность модели. По формуле (3.7) найдем дисперсию адекватности 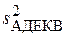= 0.3031. Как известно, величина  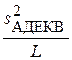= 0.0758 совпадает с остаточной дисперсией и с 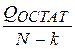. Найдём  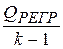= 20.622. Отсюда по (3.4) вычислим 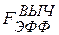= 272.144 при F^КРИТ = qF(1 – a, k –1, N – k) = 5.768. Видим, что  модель эффективна.

2) Оценим статистическую адекватность. По формуле (3.8) получим 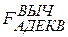= 1.697 при F^КРИТ = qF(1–a, N– k, N×(L–1)) = 2.621. Следовательно, модель адекватна.

Таким образом, получим следующую модель в безразмерных переменных:

.

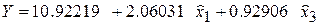Воспользуемся формулой (3.9) и вернёмся к натуральным переменным:

 =

 

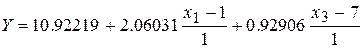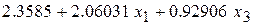
Синтез наилучшей эмпирической модели : метод исключения

Согласно изложенному материалу, регрессионная модель считается “хорошей”, если

1°. Она адекватна

2°. Она эффективна

3°. Все её коэффициенты значимы.

Степень удовлетворения всем перечисленным требованиям при выбранных экспериментальных точках зависит от варианта структуры модели, т.е. от типа модели (линейная, квадратичная или иная), а также от того, какие члены в нее включены. Типичным дефектом является наличие незначимых коэффициентов. Обычно с первой попытки хорошую модель построить не удается и надо перебирать различные ее варианты для поиска лучшей. Наиболее обоснованный и качественный вариант модели можно построить так называемым методом возможных регрессий. Согласно ему перебирают все возможные варианты структуры модели. Однако требуемый объем работы при этом весьма значителен. Более экономичен и достаточно надежен метод исключения, хотя иногда он не позволяет найти действительно наилучший вариант модели.

Согласно этому методу строят начальный вариант модели, самый сложный для данного набора экспериментальных точек, с максимальным числом коэффициентов. Оценивают её эффективность и значимость коэффициентов. Если требования 1°– 3° выполняются, то необходимая модель построена. Иначе поступают следующим образом.

Обычно среди членов модели есть незначимые, модель при этом обычно неэффективна (но может быть и эффективной). Тогда надо попытаться улучшить модель, исключив член (только один) с минимальным значением |Т _j| модуля критерия Стьюдента, пересчитать остальные коэффициенты и проверить новый вариант модели на адекватность, эффективность и значимость коэффициентов. Дальше возможны следующие случаи.

1) Если после исключения

а) адекватная модель не перестала быть таковой,

 

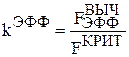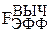б) возросла величина отношения , где проверяет эффективность текущего варианта модели и вычисляется по формуле (3.2), а F^КРИТ соответствует критическому значению распределения Фишера,

в) значение увеличилось, или уменьшилось незначительно (не более 10%),

то исключение было сделано правильно, новый вариант модели лучше предыдущего.

Если в новом варианте остались незначимые коэффициенты, то с ним можно повторить исключение, выбрав коэффициент с минимальным значением модуля критерия Стьюдента |Т _j|, и т. д.

2) Если после исключения хотя бы один из пп. а) – в) не выполнился, то исключение выбранного члена не улучшает модель. Если до исключения модель была адекватна и эффективна, то надо остановиться на её предыдущем варианте. Если при этом в модели остались незначимые коэффициенты, то в принципе, ей можно пользоваться, однако, рекомендуется проверить данные эксперимента. Возможно, в них есть грубые ошибки или просто опытов мало.

3) Если после очередного исключения в модели остался только свободный член: 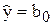, а все предыдущие варианты модели неэффективны, то это означает отсутствие связи между входом и выходом объекта, эффективную модель по имеющимся экспериментальным данным построить невозможно.

4) Модель неадекватна, отбрасывание незначимых членов не улучшает положения. Это означает, что структура модели выбрана неверно. Возможно, следует взять более сложный тип уравнения регрессии (например, вместо линейной – квадратичную).

 

Пример 3.2. Пусть объект характеризуется двумя входными параметрами х1 и х2, экспериментальные значения которых записаны в матрицу Х, и вектором у значений выхода:

; .

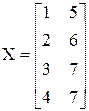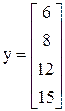Построим по этим данным линейное уравнение регрессии у = b₀ + b₁ x1 + b₂ x2.

Для этого запишем регрессионную матрицу и матрицы, связанные с ней:

; ; .

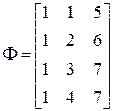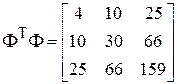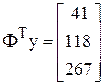В результате применения функции lsolve(Ф^ТФ, Ф^Ту) получаем вектор МНК-оценок, а с его помощью найдем вектор расчетных значений у:

;     .

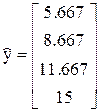Отсюда Q_ОСТАТ = 0.667; Q_ОБЩ = 48.75, следовательно, коэффициент детерминации равен 98.63%, т.е. его значение достаточно велико.

Проверим эффективность модели. F^ВЫЧ = 36.06, при a = 0.05 будет F^КРИТ = 199.5. Следовательно, модель неэффективна.

Оценим значимость коэффициентов. Для этого определим оценку дисперсионной матрицы С:

.

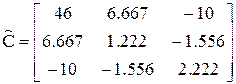Отсюда по формулам (3.3) получим вектор значений критерия Стьюдента для МНК-оценок 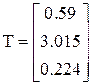 при Т^КРИТ = 12.706. Следовательно, все коэффициенты незначимы. Таким образом, несмотря на весьма удовлетворительное значение R² модель получилась “нехорошей”.

Исключим из уравнения член с минимальным |Т _j|, т.е. b₂×x2. Получим модель у =2.5 + 3.1 х1, которая является эффективной: F^ВЫЧ = 137.3, F^КРИТ = 18.5. Новые значения критерия Стьюдента равны (3.45; 11.72) при Т^КРИТ = 4.3. Следовательно, коэффициент при х1 значим, а свободный член “близок к значимому”. Коэффициент детерминации новой модели равен 98.56%, т.е. практически совпадает с показателем первоначального варианта.

 

 

Задание 2 по теме 3

Провести продвинутый анализ моделей, построенных по заданию 2 темы 2.

и выбрать лучший вариант модели.

 

РПР по теме 3

Провести моделирование технологического процесса, указанного в варианте.

ЦЕЛЬ исследования: определение оптимальных условий функционирования  технологического процесса.

ЗАДАЧИ исследования

1. Провести имитацию натурных экспериментов над исследуемым процессом с использованием ПФП и параллельных опытов.

2. Построить эмпирическую неполную квадратичную модель процесса на основе имитации натурных экспериментов.

3. Проанализировать качество синтезированных вариантов модели и методом исключения подобрать наилучшую модель.

4. Провести оптимизацию построенной целевой функции и определить оптимальные условия функционирования процесса.

5. Провести сравнение полученного результата с базовым (используемым в настоящее время) вариантом и убедиться в преимуществе нового варианта условий протекания процесса.

6. Разработать программное обеспечение автоматизации процесса моделирования в виде документа MathCad и написать отчёт о проведённой НИР. Отразить в выводах по работе результативность проделанной НИР.

 

 

ОБРАЗЕЦ ВЫПОЛНЕНИЯ РПР – Модель № 99

(В этом пункте необходимо описать исследуемый процесс:

- его название;

- перечень входных параметров и диапазона их изменения;

- название выходного параметра и пояснить, как его значение связано с качеством исследуемого процесса;

- указать базовый вариант функционирования процесса)

 

 

Исходные данные:

           Матрицы плана экспериментов                             Вектор базисных функций

в реальных переменных в безразмерных переменных

 

                                                                     

 

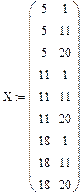
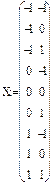
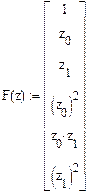
В результате имитации 5 параллельных опытов получаем следующие данные:

 

 

Матрица результатов эксперимента         Усреднённые показатели:

 

                          

 

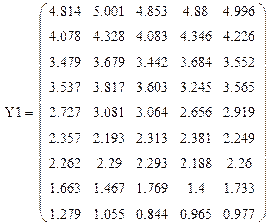
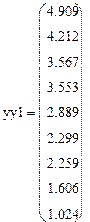
Проверяем однородность точечных дисперсий:

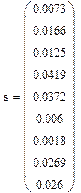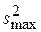 , = 0.0419,  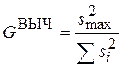 = 0.238. По таблице ПРИЛОЖЕНИЯ 2 находим G^ТАБЛ (0.05, 9, 4) = 0.3584. Дисперсии однородны.

С помощью МНК получаем следующий вектор коэффициентов

 

 

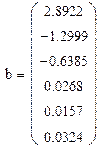
Значения критерия Фишера Fэфф =391.936 и коэффициента эффективности Kэфф = 43.483. Значения критерия Стьюдента 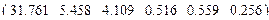.  Три последних значения незначимы, т.к. qt(0.975,9×4) = 2.028.  В процессе реализации метода исключения они будут отброшены. (Для краткости этот процесс в образце опустим).

В результате применения метода исключения получаем следующую модель в безразмерных переменных 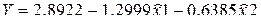, или после подстановки .

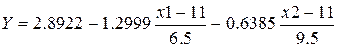После преобразования получим модель в натуральных переменных

Y = 5.8313 – 0.19998 x1 – 0.067211 x2.

Для поиска максимума Y(x) воспользуемся следующей последовательностью операторов MathCad

 

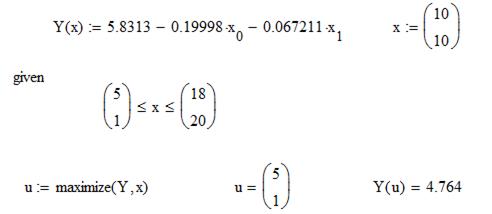
Таким образом, максимум достигается в точке (5; 1), что соответствует значению целевой функции 4.764. По сравнению с базовым вариантом x = (10; 10),

Y(x) = 3.236 получен выигрыш в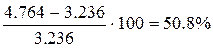

 

Выводы

В процессе проведённой НИР получены следующие основные результаты.

1. По результатам имитации моделируемого процесса с помощью программы Imitator проанализировано 4 варианта математической модели процесса. Выбран лучший вариант эмпирической модели, описывающей аналитическую зависимость выходного параметра от входных.

2. Решена задача оптимизации, использующая выходной параметр в качестве целевой функции. В результате найдены оптимальные условия функционирования процесса x^opt = (5; 1), что даёт значение выходного параметра 4.764.

3. По сравнению с базовым вариантом увеличение значения выходного параметра составило 50.8%, что показывает существенное улучшение условий функционирования процесса.

4. Разработано программное обеспечение автоматизации процесса моделирования в виде документа MathCad (прилагается к отчёту).

Задачи исследования решены, цель достигнута.

 

 

ПРИЛОЖЕНИЕ 1

---

Дата добавления: 2019-02-26; просмотров: 244; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!