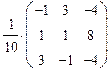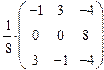Случайные векторы и их характеристики

Тема 1. Математическое и программное обеспечение процесса

Моделирования

Линейная алгебра

Повторите основные понятия линейной алгебры: линейное пространство, векторы, линейная комбинация векторов, линейная зависимость векторов, матрицы, ранг матрицы, действия с матрицами, обратная и транспонированная матрица, вычисление определителя.

1. Свойства матриц и матричных операций

1. I – единичная матрица

2. det A – определитель матрицы А. Если det A = 0, то А – вырожденная матрица, иначе А невырождена.

3. Вычисление произведения двух матриц и матрицы на столбец

Пусть даны две матрицы: A размера n строк и m столбцов, B размера m строк и k столбцов, а также столбец Х из m элементов. Надо вычислить произведения С = A×B и Y = A×X.

В основе вычислительных алгоритмов лежат следующие формулы:

; ;

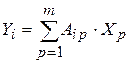i = 1,….n; j = 1,…k.

4. A^T – транспонированная матрица.

Свойства : (A + B)^T = A^T + B^T; (A B)^T = B^T A^T.

5. Если А – квадратная невырожденная матрица, то A^–1 – обратная матрица, такая, что AA^–1 = A^–1A = I.

Свойства: (A B)^–1 = B^–1A^–1; (A^T)^–1 = (A^–1)^T; (A^ТA) – симметричная матрица.

6. Линейная комбинация векторов a¹, a², …, a^k – это выражение вида

l₁×a¹ + l₂× a² + … + l_k×a^k , где l_i×– числа, не все равные 0.

Пусть, например, 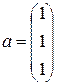; ; 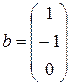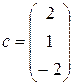. Пример линейной комбинации: 1×a + 1×b + 1×c = .

7. Ненулевые векторы называются линейно зависимыми, если существует их линейная комбинация, равная нулевому вектору.

Пусть, например, ; ; 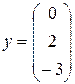. Векторы x, y, z линейно зависимы, т.к. z = x – y. Отсюда 1×x – 1×y – 1×z = 0.

8. Ранг матрицы А – целое число rank A, равное максимальному порядку отличного от 0 минора матрицы.

Например, матрица 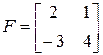невырождена. Следовательно, максимальный порядок её ненулевого минора равен 2, т.е. размерности матрицы. Значит, rank F = 2.

Матрица 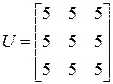имеет ненулевые миноры лишь 1-го порядка, все равные 5. Значит, rank U = 1.

Задачи для самостоятельного решения

1. Дано: . Вычислить det (A) разложением по 1-й строке.

2. Дано: . Вычислить det (A) разложением по 3-му столбцу.

3. Дайте определение понятия «линейная комбинация векторов». Образуйте любую линейную комбинацию из векторов

; ; .

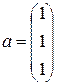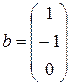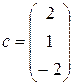4. Какие векторы называются линейно зависимыми, а какие – линейно независимыми? Являются ли линейно зависимыми следующие три вектора

; ; .

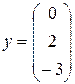5. Что такое «ранг матрицы»? Чему равны ранги следующих матриц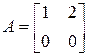

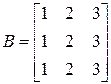
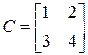? Ответ объяснить.

6. Какая из следующих матриц является обратной к матрице C = :

Ответ объяснить.

7. Дано: ; 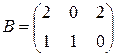. Вычислить B А ^T A.

Основные сведения из теории вероятностей

Def . Случайное событие – некоторое событие, которое в результате опыта при выполнении определённых условий может наступить, а может не наступить.

Замечание. Следует отметить, что с точки зрения исследователя, наблюдающего это события, каждый раз условия опыта абсолютно одинаковы, тем не менее, в одном случае событие наступает, а в другом – нет. Это происходит из-за того, что мы не знаем о существовании каких-то факторов, влияющих на событие, или знаем, но не можем их зафиксировать.

Тем не менее, факт наступления случайного события подчиняется определённой закономерности.

Def . Вероятность случайного события А – величина P(А), 0 £ P(А) £ 1, определяющая объективную возможность наступления случайного события. Событие называется достоверным, если при выполнении определённых условий оно всегда наступает, его вероятность равна 1. Событие называется невозможным, если при выполнении определённых условий оно никогда не наступит, его вероятность равна 0.

Def . Случайная величина (СВ) – это величина, которая в результате опыта может принимать те или иные значения, неизвестные заранее.

Случайная величина x может принимать такие значения, которые можно перенумеровать – х₁, х₂ и т.д. Такие случайные величины называются дискретными. Пример – число очков, выпадающих на игральной кости. Непрерывными называются СВ, возможные значения которых заполняют сплошь некоторую область числовой оси. Пример – значение температуры некоторого тела.

Def . Закон распределения случайной величины – это любое соотношение, устанавливающее связь между возможным значением случайной величины и соответствующей вероятностью принятия этого значения.

Законы распределения имеют следующие формы.

Для дискретной СВ необходимо задать соответствие между возможными значениями x = х₁, x = х₂, … случайной величины и вероятностями Р(x= х_i) = p_i, с которой эти значения принимаются. Задать это соответствие можно таблично, аналитически (в виде формулы) и графически.

Пример 1.1. Пусть бросаются две игральные кости. СВ x – число выпадений «орла». Очевидно, возможны следующие значения x : х₁ = 0; х₂ = 1; х₃= 2. Несложно подсчитать, что соответствующие вероятности равны: р₁ = 1/4; р₂ = 1/2; р₃= 2. Составим таблицу:

х_i	0	1	2
р_i	1/4	1/2	1/4

которая представляет собой табличное задание закона распределения СВ x = (число выпадения «орла» на двух игральных костях).

Для непрерывной СВ существуют следующие формы записи закона распределения: функция распределения и плотность распределения.

Def . Функцией распределения случайной величины x называется функция F(х) = F _x (х) = P(x < x), которая определяет вероятность того, что случайная величина x примет значение, меньше фиксированного неслучайного числа x, т.е. наступит событие x < x.

Свойства F ( x ).

1. F(х) – неубывающая функция, удовлетворяющая условию 0 £ F(x) £ 1, F(–∞) = 0, F(∞) = 1.

2. Вероятность попадания случайной величины в заданный интервал [a, b] равна: P(a £ x £ b) = F(b) – F(a).

Def . Плотностью распределения случайной величины x называется функция f(x) = f _x (x) = 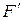(х).

Свойства f ( x ).

1. 0 £ f(x) для любого х.

2. Формула обращения:

. (1.1)

3. 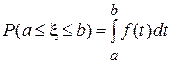– аналог свойства 2 F(x).

4. 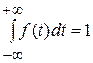– условие нормировки.

Квантиль. Часто возникает задача по известной вероятности р определить значение b, при котором р = Р(x < b) = F_x (b). Для её решения необходимо найти обратную функцию F^(–1)_x (у) к F_x (х). Тогда b = t _p = F^(–1)_x (p). Вычисляемая по этой формуле величина t _p называется р-квантилем данного закона распределения.

Для вычисления р-квантиля можно воспользоваться функцией MathCad q Имя_Распределения (P, параметры), см. 1.3. Статистические функции MathCad .

Например, вычислим 0,25-квантиль экспоненциального распределения с параметром l =2, т.е. для распределения с плотностью f(x) = 2exp(-2x). Воспользуемся операторами MathCad

tp:=qexp(0.25, 2) tp = 0.14384

Проверяем: Р(x < tp) = F_x (tp) = .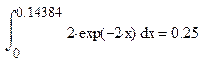

Числовые характеристики случайной величины. Закон распределения СВ является её исчерпывающей характеристикой. Однако получить его достаточно трудно. Поэтому часто для изучения свойств СВ используют их числовые характеристики (параметры).

Def . Числовые характеристики (параметры) СВ – некоторые неслучайные величины, значения которых характеризует определённое свойство СВ.

Примеры параметров СВ.

1. Математическое ожидание (МО) – характеризует среднее значение, принимаемое СВ (центр тяжести).

Вычислительные формулы:

М[x] = m_x = – для дискретной СВ;

М[x] = m_x = 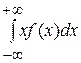– для непрерывной СВ.

Отметим свойства математического ожидания:

1. Если с – неслучайная величина, то M[c] = c.

2. Если x – СВ, а с – неслучайная, то M[c×x] = c×M[x].

3. M[x + h] = M[x] + M[h].

4. Из свойства 3 следует: если x – СВ, то h = x – M[x] – это СВ, у которой M[h] = 0.

2. Дисперсия. – характеризует среднюю величину разброса значений СВ относительно МО.

Вычислительные формулы:

D[x] = – для дискретной СВ;

D[x] = D_x = 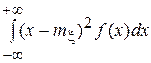– для непрерывной СВ.

Величина v = называется среднеквадратичным отклонением.

Отметим свойства дисперсии.

1. Если с – неслучайная величина, то D[c] = 0.

2. Если x – СВ, а с – неслучайная, то D[c×x] = c² ×D[x].

3. Если x и h – независимые СВ, то D[x + h] = D[x] + D[h].

4. Из свойства 2 следует: если x – СВ, то h = – это СВ, у которой D[h] = 1.

5. Справедлива формула D[x] = M [ (x – M[x]) ²] = M[x²] – (M[x])².

Кроме математического ожидания и дисперсии важной числовой характеристикой СВ является коэффициент вариации – безразмерный показатель разброса случайной величины.

Случайные векторы и их характеристики

Def . Случайным вектором называется вектор, координатами которого являются случайные величины: = .

Набор (x₁,…, x_n) называют также системой случайных величин. Как и обычные (скалярные) случайные величины, случайные векторы бывают непрерывными и дискретными. Исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения (функция совместного распределения системы случайных величин).

Def . Функция распределения F(x₁,…, x_n) случайного вектора равна вероятности следующего сложного события: {( x₁< x₁) Ù … Ù ( x_n< x_n)}.

Дата добавления: 2019-02-26; просмотров: 704; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!