Def. Плотностью совместного распределения системы случайных величин (плотностью распределения случайного вектора) называется функция
.
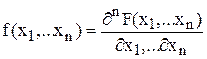Def . Случайные величины называются независимыми, если закон распределения любой из них не зависит от того, какие значения приняли другие величины.
Теорема 1.1 (о независимости случайных величин). Для того чтобы случайные величины x1,…, xn были независимы необходимо и достаточно, чтобы выполнялось равенство:
F(x1,…, xn) = F1(x1) ×…× Fn(xn),
где F1(x1) ,…, Fn(xn) – индивидуальные законы распределения случайных величин x1,…, xn.
Следствие. Для того, чтобы случайные величины x1,…, xn были независимы необходимо и достаточно, чтобы выполнялось равенство:
f(x1,…, xn) = f1(x1) ×…× fn(xn),
где f1(x1) ,…, fn(xn) – индивидуальные плотности распределения случайных величин x1,…, xn.
Def. Математическим ожиданием случайного вектора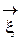 
называется вектор 
.
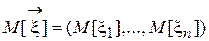Def. Ковариацией случайных величин x1 и x2 называется величина
cov(x1, x2) = M [(x1 – M[x1] ) × (x2 – M[x2])].
При x1 = x2 ковариация x1 и x2 равна дисперсии x1, т.е. D[x1]. При x1 ¹ x2 ковариация x1 и x2 показывает тесноту связи x1 и x2. Если x1 и x2 независимы, то их ковариация равна нулю.
Если при возрастании или убывании одной из xi и другая величина ведет себя аналогично (т.е. возрастает или убывает вместе с первой величиной), то cov(x1, x2) > 0. Если же возрастание одной величины сопровождается убыванием другой, то cov(x1, x2) < 0. Для любых x1 и x2 справедливо неравенство
0 £ |cov(x1, x2)| £ 
.
Def . Ковариационной (дисперсионной) матрицей случайного вектора 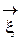называется матрица D[ 
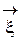], элементы которой D i j равны cov(xi, xj).
|
|
|
Одна важная теорема. В статистическом моделировании большое значение имеет следующая теорема.
Теорема 1.2 (о линейно зависимых случайных векторах). Пусть между случайными векторами 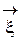и 
и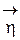меет место линейная функциональная зависимость h = Аx, где А – некоторая прямоугольная матрица (m строк и n столбцов). Тогда
1) M[h] = A × M[x];
2) D[h] = A D[x] A T.
Задачи для самостоятельного решения
8. Случайная величина x задана функцией распределения
F(х)=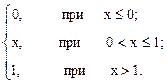 
Определить вероятность того, что в результате испытаний случайная величина примет значение, большее 0,5, но меньшее 0,8. Найти f(x), М[Х], D[X].
9. Плотность распределения вероятностей случайной величины Хзадается соотношением
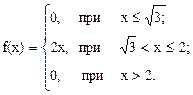
Найти функцию распределения и построить графики f(x), F(x).
10. Дана функция
f(х)=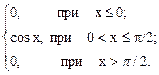 
Может ли эта функция быть плотностью распределения некоторой случайной величины (обосновать ответ)? Если да, то какова вероятность того, что случайная величина примет значение из интервала (p/4; p/3)?
11. Дана функция
F(х)=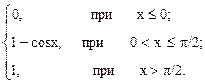 
Найти f(x). Построить графики f(x), F(x).
12. Функция f(x) задана выражением
f(х)= 
Найти С и F(х). Построить графики этих функций. Найти вероятность попадания случайной величины в интервал (0,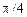 
).
|
|
|
13. Найти математическое ожидание и дисперсию случайной величины X, если плотность вероятностей ее
f(х)=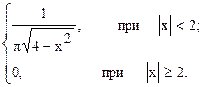 
14. Доказать, что среднее арифметическое n независимых одинаково распределённых случайных величин 
= (x1 + … + xN ) / N обладает следующими свойствами
а) M[ ] = M[xi], i = 1, 2, …N.
б)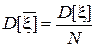 
.
Указание. Воспользоваться теоремой 1.2, положив h = .
Дата добавления: 2019-02-26; просмотров: 226; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!