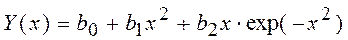Получение статистических оценок параметров уравнения регрессии. МНК
Пример 2.2.
| Построить модель вида | |||||||
|
| |||||||
| по следующим экспериментальным данным: | X | Y | |||||
| 0,5 | 2,64 | ||||||
| 1 | 2,82 | ||||||
| 1,5 | 1,86 | ||||||
| 2 | 1,62 | ||||||
| 2,5 | 1,72 | ||||||
| 3 | 1,96 | ||||||
| 3,5 | 2,24 | ||||||
| 4 | 2,59 | ||||||
| 4,5 | 3,06 | ||||||
| 5 | 3,53 | ||||||
Решение.
1 . Строим регрессионную матрицу
| Ф = |
|
2. Находим оценки коэффициентов с помощью оператора MathCad
b := lsolve (ФTФ, ФT у),
где 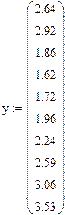 – вектор экспериментальных значений параметра y.
– вектор экспериментальных значений параметра y.
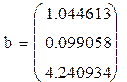
3. Находим значения 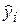 аппроксимирующей функции
аппроксимирующей функции

4. Строим графики исходных данных и аппроксимирующей функции
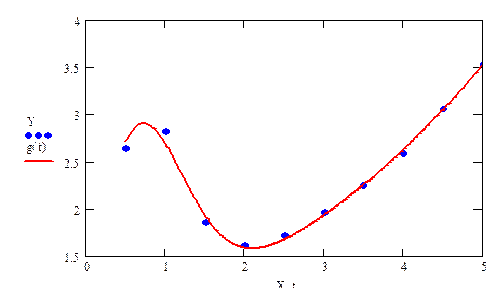
5 . Вычисляем показатели качества регрессии:
а) остаточную дисперсию 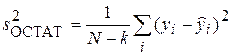 = 0.004359.
= 0.004359.
б) коэффициент детерминации 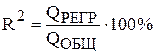 = 99.144%,
= 99.144%,
где QОБЩ = å(уi – 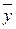 )2; QРЕГР = å
)2; QРЕГР = å  2.
2.
в) оценку дисперсии МНК-прогноза: 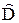 [
[  (х)] =
(х)] = 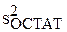 fT(x) (ФT Ф)–1f(x) и её максимальное значение = 0.0027447 на отрезке [0.5; 5].
fT(x) (ФT Ф)–1f(x) и её максимальное значение = 0.0027447 на отрезке [0.5; 5].
Задание 2 по теме 2.
Для следующих вариантов наборов экспериментальных данных, содержащих случайные ошибки:
1) построить аппроксимирующую функцию Y1, используя имеющийся в задании набор базисных функций
2) построить квадратичную аппроксимирующую функцию Y2 = ax2 + bx + c.
3) построить таблицы и графики экспериментальных данных и обеих аппроксимирующих функций, оценить величины
а) остаточной дисперсии,
б) значение коэффициента детерминации,
в) максимальное значение дисперсии МНК-прогноза для каждой модели.
4) По значениям а) – в) выбрать лучшую из двух полученных моделей.
1.
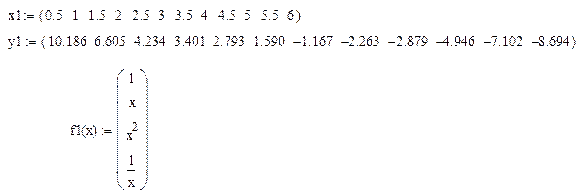
2.
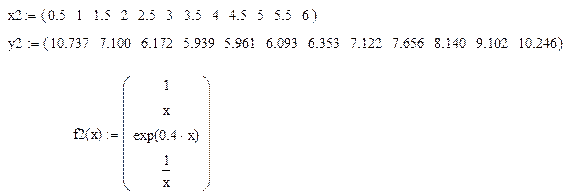
3.
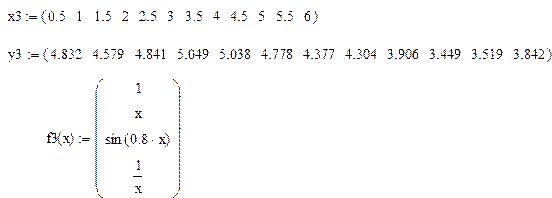
4.
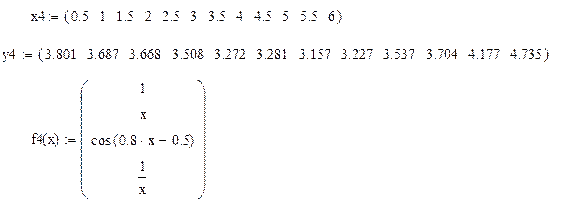
5.
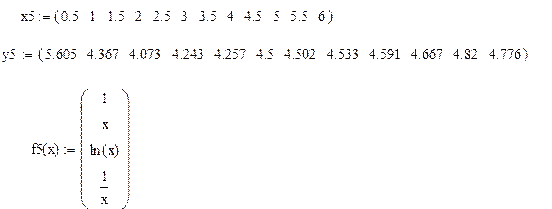
6.

7.
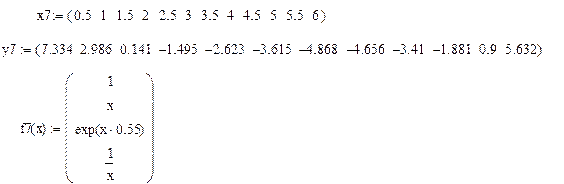
8.

9.
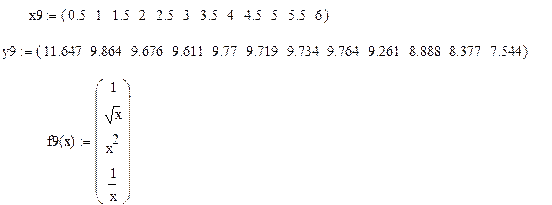
10.
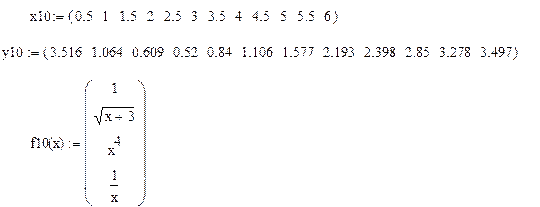
11.
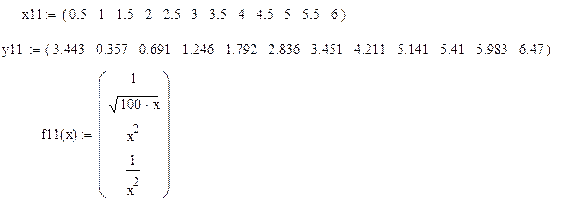
12.
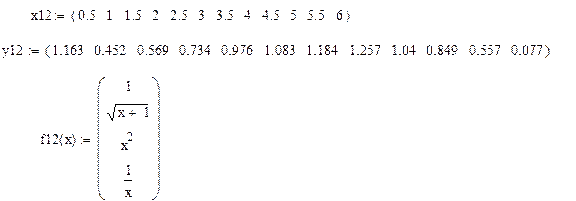
13.
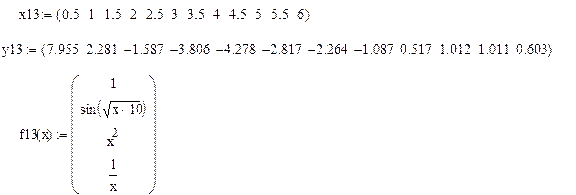
14.

15.
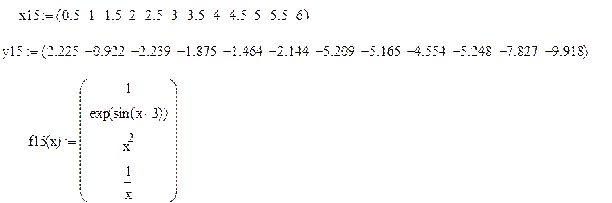
16.

Тема 3. Проверка статистических гипотез и её приложение к регрессионному анализу
Def . Статистическая гипотеза – некое суждение о свойствах случайной величины. Проверка статистической гипотезы – процедура сопоставления выбранной гипотезы с имеющимися экспериментальными данными, сопровождаемая количественной оценкой степени достоверности полученного вывода.
Технология проверки статистических гипотез
1. Проводится серия экспериментов для получения статистического материала.
2. По полученным данным выдвигается статистическая гипотеза.
3. Задаётся уровень значимости a – максимально допустимая вероятность ошибки (в технических задачах принято выбирать a = 0.05), определяется тип выдвинутой гипотезы и соответствующий статистический критерий К. По виду гипотезы и значению a определяется критическая область V КР.
4. По экспериментальным данным вычисляется значение КВЫЧ.
5. Если КВЫЧ попадает в V КР, то основная гипотеза отвергается, в противном случае – принимается.
Замечание. Принятие определенной статистической гипотезы не означает, что она является наилучшей или единственной. Просто данная гипотеза не противоречит имеющимся данным. Таким же свойством могут обладать и другие гипотезы. Отклонение же гипотезы носит более категоричный характер: она противоречит нашим экспериментальным данным и, следовательно, почти наверняка (с вероятностью не менее 1 – a) – неправильная.
К ритерий Пирсона
c 2-распределение Пирсона (хи-квадрат).
Def . Пусть имеем случайный вектор xÎN(0, I n), где I n – единичная матрица порядка n. Тогда скалярная СВ h = xТx =  имеет распределение Пирсона с n степенями свободы (n – параметр распределения). Будем обозначать это hÎc2(n).
имеет распределение Пирсона с n степенями свободы (n – параметр распределения). Будем обозначать это hÎc2(n).
Использование критерия Пирсона. Пусть имеем набор статистических данных о некоторой случайной величине. Есть предположение, том, каков закон распределения этой величины. Необходимо проверить эту гипотезу на основании имеющихся данных. Наиболее часто для решения этой задачи используется критерий Пирсона c2.
Идея метода. Пусть  – реализация выборки некоторой скалярной случайной величины x. Обозначим
– реализация выборки некоторой скалярной случайной величины x. Обозначим 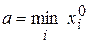 ;
;  – минимальный и максимальный элементы выборки, соответственно. Разобьем полученную область [a, b] значений элементов выборки на m частей (m ³ 2), обозначив их D1,…, Dm. Пусть F(x) – предполагаемая функция распределения. Введем следующую статистику
– минимальный и максимальный элементы выборки, соответственно. Разобьем полученную область [a, b] значений элементов выборки на m частей (m ³ 2), обозначив их D1,…, Dm. Пусть F(x) – предполагаемая функция распределения. Введем следующую статистику
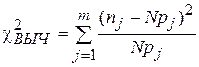 , (3.1)
, (3.1)
где:
- n j – число элементов выборки, попавших в Dj;
- p j – теоретическая вероятность попадания в Dj СВ, распределенной по закону F(x).
Теорема о критерии Пирсона. Если СВ x имеет функцию распределения F(x), то при N ® ¥ распределение СВ  стремится к распределению Пирсона с n = m – k – 1 степенями свободы, где k – число параметров функции F(x), оценки которых найдены по данной выборке.
стремится к распределению Пирсона с n = m – k – 1 степенями свободы, где k – число параметров функции F(x), оценки которых найдены по данной выборке.
Более подробное описание. Обозначим a = z0 , z1 , …, z m = b – точки, разбивающие [a, b] на m частей, z – вектор с компонентами z j. Тогда Dj = [z j–1, z j ].
Для подсчёта чисел n j можно воспользоваться функцией MathCad hist. Обращение к ней выглядит так: n := hist(z, X), где Х – вектор с элементами выборки. Функция возвращает вектор n, компонентами которого являются nj, см. файл ‘ХИ образец.mcd’.
Для определения pj воспользуемся известной формулой тории вероятностей о вероятности попадания случайной величины в заданный интервал:
P(xÎ[u, v] ) = Fx(v) – Fx (u). (3.2)
В нашем случае p j = P(xÎDj) = F(z j) – F(z j–1).
Чтобы иметь возможность вычислить значения F(x) надо знать её числовые параметры. Для поиска оценок числовых параметров функции F(x) можно воспользоваться каким-либо известным методом нахождения статистических оценок, например – методом максимального правдоподобия.
Найденные таким образом n j и p j подставим в формулу (3.1). Если F(x) – предполагаемый закон распределения, то проверка этого факта сводится к проверке соответствующей статистической гипотезы с правосторонней критической областью (t1–a , +¥), где t1–a – критическое значение распределения Пирсона, которое находится с помощью функции MathCad qchisq. Обращение к ней выглядит так: t := qchisq(1– a, m – k – 1). При  принимается гипотеза о том, что F(x) действительно является функцией распределения СВ x. В противном случае гипотеза отвергается.
принимается гипотеза о том, что F(x) действительно является функцией распределения СВ x. В противном случае гипотеза отвергается.
Пример применения критерия Пирсона для проверки гипотезы о нормальном законе распределения см. ПРИЛОЖЕНИЕ 1.
Достоинство метода. Главное достоинство критерия c2 в том, что он применим к любой функции распределения.
Недостаток. Поскольку, согласно теореме, распределение Пирсона для статистики c2 имеет место лишь в пределе, то ограничительным условием применения данного критерия является достаточно большой объем выборки. На практике он используется, когда для всех n j справедливо неравенство n j ³ 5. Исходя из этого соображения, определяется число m интервалов. Если данное неравенство не выполняется, то соседние интервалы необходимо объединить, так, чтобы условие выполнялось.
Задание 1 по теме 3
Используя данные своего варианта определить закон, по которому распределены эти данные.
Порядок выполнения
1. Считываем данные из файла своего варианта.
2. Строим гистограмму, используя функцию hist. Если условие n j ³ 5 не выполняется, производим объединение интервалов.
3. По виду графика гистограммы выдвигаем гипотезу о предполагаемом законе распределения. Возможны следующие варианты
а) Равномерный закон
б) Показательный закон
в) Логарифмически нормальный закон
Графики и формулы их плотностей распределения приведены в 1.2.
4. Выводим формулы ММП-оценок параметров предполагаемого распределения (образец – задача № 25).
5. Вычисляем p j по формуле (3.2).
6. Вычисляем значения 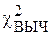 по формуле (3.1) и
по формуле (3.1) и  с помощью функции qchisq.
с помощью функции qchisq.
7. Делаем вывод о правильности выдвинутой гипотезы.
8. Строим совместный график теоретического и эмпирического (гистограммы) распределений для их визуального сравнения.
Дата добавления: 2019-02-26; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!