Динамика относительного движения материальной точки.

 

Понятие о силе инерции.

 

Пусть материальная точка M движется под действием силы F с ускорением a . F сила, с которой т. М₁ действует на т. М. Действие т. М₁ на т. M будет определяться 2-м

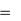
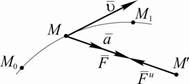
законом динамики F   ma .

 

По закону равенства действия и противодействия со стороны т. М на т. М₁ будет

 

действовать сила F ^и , равная по модулю силе F и направленная по той же прямой в противоположную сторону, т. е.

и

.

F

F

Или

и

m

F

(1)

a

Модуль силы

и

m a

F

(2)

 

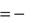
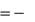
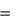
Равенства (1) и (2) и определяют силу инерции.

 

Силой инерции материальной точки называется сила,равная по модулюпроизведению массы материальной точки на модуль ее ускорения, направленная противоположно ускорению и приложенная к телу, сообщающему это ускорение.

 

В том случае, когда движется несвободная материальная точка, ее сила инерции приложена к связям, наложенным на эту точку.

 

Виды сил инерции точечной массы.

 

Существует столько видов сил инерции точечной массы, сколько имеется видов ускоренной точки.

 

Полная сила инерции F ^и 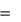 m a ;

Касательная сила инерции F ^и 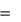 m a ;

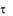
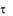
Нормальная сила инерции F _n ^и 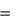 m a _n ;

В случае сложного движения точки:

относительная сила инерции F _r ^и 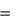 m a _r ;

 

переносная сила инерции F _е ^и 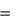 m a _е ;

кориолисова сила инерции F _k ^и 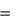 m a _k .

В свою очередь относительная и переносная силы инерции могут быть нормальными

и касательными: F _rn ^и , F _r ^и , F _en ^и , F _e ^и_τ .

 

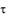
Дифференциальные уравнения относительного движения

Материальной точки.

 

12

Рассмотрим случай, когда материальная точка движется относительно подвижной системы координат oxyz, называемой неинерциальной.

 

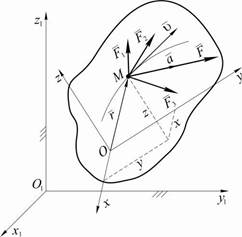
Инерциальной системой отсчета называется неподвижная система координатo₁x₁y₁z₁,чаще всего связанная с землей.

 

Пусть т. М совершает сложное движение. 1-ый и 2-ой законы динамики справедливы только для абсолютного движения т. М, т.е. для движения относительно инерциальной системы отсчета. Изучим (рассмотрим) динамику относительного движения т. М, т. е. движение относительно неинерциальной системы отсчета, т. е. подвижной системы координат oxyz.

 

Запишем основное уравнение динамики

 

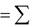
m			F i	(1)
	a

Так как точка совершает сложное движение, то ее полное (абсолютное) ускорение по теореме Кориолиса будет равно

 

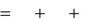
				r		e		k	(2)
	a		a		a		a

 

Тогда уравнение (1) можно переписать в виде

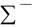
ma _r ma _e ma _k 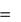  F _i

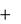
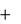
или

ma _r 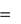  F _i ma _e ma _k

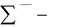
Так как

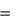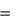F _е ^и  m a _е , F _k ^и  m a _k ,

то

m							и		и
				F		F		F		(3)
	a
	r			i		e		k

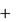
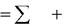
Выражение (3) является основным уравнением динамики относительно движения точки.

 

Вывод. Все уравнения механики для относительного движения материальной точки составляются также, как и уравнения для абсолютного движения, но при этом к действующим на точку силам нужно добавлять переносную и кариолисову силу инерции, которые прикладываются к точке условно.

 

Так как

_a ^d r^d2r _, dt dt ²

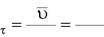
то уравнение (3) можно записать в следующем виде

 

13

d

r

и

и

m

F i

F e

F k

(4)

dt

или

m

d2

r

и

и

(5)

F

F

F

dt 2

i

e

k

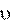
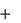
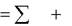
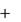
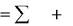
Выражения (4) и (5) представляют собой дифференциальные уравнения относительного движения точки в векторной форме соответственно 1-го и 2-го порядка.

 

Спроектируем уравнения (4) и (5) на оси подвижной системы координат, тогда получим:

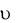
d rx

и

и

m

X i

F ex

F kx

dt

m

d ry

Y

F

и

F

и

(6)

dt

i

ey

ky

d rz

и

и

m

Z i

F ez

F kz

dt

или

m

d2 x

X

и

и

i

F

F

dt 2

ex

kx

m

d2 y

Y

и

и

(7)

F

F

dt 2

i

ey

ky

m

d2 z

Z

и

и

F

F

dt 2

ez

kz

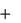
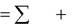
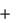
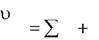
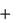
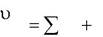
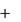
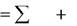
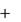
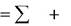
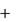
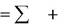
Полученные выражения (6) и (7) являются дифференциальными уравнениями относительного движения точки в декартовых координатах (в координатной форме) соответственно 1-го и 2-го порядка.

 

---

Дата добавления: 2019-02-26; просмотров: 433; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!