Линейная зависимость векторов. Разложение вектора по базису.
Линейная зависимость векторов.
Определение. Векторы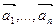 
называются линейно зависимыми, если существует такая линейная комбинация 
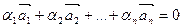, при не равных нулю одновременно a i , т.е. 
.
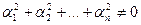Если же только при a i = 0 выполняется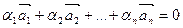 
, то векторы называются линейно независимыми.
Свойство 1. Если среди векторов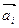 
есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Определение.
Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
Базисом на прямой называется любой ненулевой вектор.
Определение. Если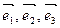 
- базис в пространстве и 
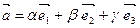, то числа a , b и g - называются компонентами или координатами вектора 
в этом базисе.
|
|
|
Основное значение базиса состоит в том, что линейные операции над векторами в заданном базисе сводятся к аналогичным линейным операциям над числами – координатами вектора в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
= 
.
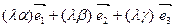- при сложении векторов складываются их соответствующие компоненты.
; 
;
+ 
= 
.
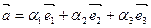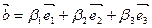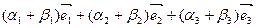На практике удобно использовать единичные базисные векторы, лежащие на взаимно перпендикулярных осях: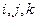 
.
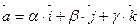Формула выражает разложение вектора по базисным векторам 
.
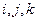Декартова система координат. Координаты вектора.
Система координат.
Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса.
Декартова система координат.
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.
Вектор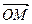 
назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.
Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
|
|
|
Я ось – ось абсцисс
Я ось – ось ординат
Я ось – ось апликат
Дата добавления: 2019-02-12; просмотров: 201; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!