Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А( x ₁ , y ₁ , z ₁ ), B ( x ₂ , y ₂ , z ₂ ), то 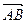= ( x ₂ – x ₁ , y ₂ – y ₁ , z ₂ – z ₁ ).

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

       Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

Декартовыми прямоугольными координатами  вектора  называются его проекции на координатные оси

.

, т.е. вектор  имеет координаты .

Равные векторы имеют равные координаты, поэтому координаты вектора не зависят от его положения в пространстве.

      

Линейные операции над векторами в координатах.

Пусть заданы векторы в прямоугольной системе координат

 тогда линейные операции над ними в координатах имеют вид:

Направляющие косинусы, длина вектора.

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y ₁ , z ₁ ), B ( x ₂ , y ₂ , z ₂ ), то .

Направляющими косинусами вектора называются косинусы углов , образуемых им с координатными осями.

Принимая во внимание формулу , для вектора  получаем

Из полученных формул и формулы нахождения длины вектора находим формулы для направляющих косинусов вектора :

.

Возводя в квадрат и почленно складывая, имеем:

; следовательно, сумма квадратов направляющих косинусов вектора равна 1.

Из формул 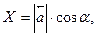 следует, что координаты единичного вектора равны его направляющим косинусам.

Деление отрезка в данном отношении.

Если точка М(х, у, z ) делит отрезок АВ в соотношении l , считая от А, то координаты этой точки определяются как:

       В частном случае координаты середины отрезка находятся как:

x = ( x ₁ + x ₂ )/2;    y = ( y ₁ + y ₂ )/2;       z = ( z ₁ + z ₂ )/2.

Если l отрицательна, значит точка М лежит на продолжении отрезка АВ.

Скалярное произведение векторов, его свойства, вычисление и применение.

       Определение. Скалярным произведением векторов  и  называется число, равное произведению длин этих сторон на косинус угла между ними.

×  = ï ïï ï cos j

                                       

       Свойства скалярного произведения :

1) ×  = 0, если ^  или = 0 или  = 0 ;

2) ×  = × ;

3) × ( + ) = × + × ;

4) (m ) ×  = × (m ) = m( × ); m=const .

Следствие. ×  = ï ï ²

       

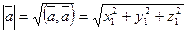
Если рассматривать векторы в декартовой прямоугольной системе координат, то

×  = x_a x_b + y_a y_b + z_a z_b;

Используя полученные равенства, получаем формулу для вычисления угла между векторами:

;

      

      

      

Векторное произведение векторов, его свойства, вычисление и применение.

Скажем, что тройка векторов , ,  правая, если кратчайший поворот от вектора  к вектору  против часовой стрелки (если наблюдать с конца вектора ).

                              

                                      

                                          

                                       

Левая тройка векторов (кратчайший поворот от  к  по часовой стрелке).

Определение. Векторным произведением векторов  и  называется вектор , удовлетворяющий следующим условиям:

1) , где j - угол между векторами и ,

2) вектор ортогонален векторам и

3) , и  образуют правую тройку векторов.

Обозначается:  или .

Свойства векторного произведения векторов:

1) ;     ( а * а = 0 );

2) , если ïï (коллинеарны) или = 0 или = 0;

3) ( m ) ´ = ´ ( m ) = m ( ´ );

4) ´ ( + ) = ´ + ´ ;

5) Если заданы векторы ( x_a , y_a , z_a ) и ( x_b , y_b , z_b ) в декартовой прямоугольной системе координат с единичными векторами , то

´ =

6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

      

---

Дата добавления: 2019-02-12; просмотров: 323; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!