Нормальное распределение случайных величин.

⇐ ПредыдущаяСтр 2 из 17Следующая ⇒

Пусть р - вероятность появления некоторого события в единичном испытании. Тогда вероятность того, что событие появится в п испытаниях ровно т раз определяется формулой Бернулли:

(12)

где - число сочетаний из псобытий по т.

Формула (12) является аналитическим выражением закона биномиального распределения случайных величин.

При большом числе испытаний (n → ∞) распределение (13) преобразуется в непрерывное распределение плотности вероятности, называемое нормальным, или гауссовым распределением с параметрами <x> и σ.

Функция Гаусса имеет следующий вид:

(13)

где <x>- среднее значение или математическое ожидание величины х;

σ - стандартное отклонение, которое определяется как

(14)

В физике величину σ принято называть среднеквадратичным отклонением от < x >.

Величина D называется дисперсией и может быть вычислена интегрированием квадратов отклонений от <x> по всему интервалу возможных значений х:

(15)

6. Возможности определения функции плотности вероятности.

Функцию плотности вероятности можно было бы найти из эксперимента, если иметь бесконечное число результатов измерений. В реальном случае, при конечном числе измерений, строят гистограммы. Для этого область значений наблюдаемой величины х разбивается на равные интервалы ширины h, подсчитывается число случаев v попадания величины х в данный интервал (говорят, что данные группируются), и на каждом интервале строят прямоугольник высоты v/N, где N - полное число измерений. Выборочное среднее определяется по формуле (1), а выборочное стандартное отклонение - по формуле

(16)

При большом числе измерений N и при достаточно малом h высоты прямоугольников можно рассматривать как приближенные значения плотности вероятности f( х ) в средних точках соответствующих интервалов, а линию, проведенную через эти точки - кривой распределения. Примером такого распределения может служить кривая, представленная на рис.3

Рис. 3. Гауссово распределение. Точки перегиба соответствуют

x = <x> ± σ.

Свойства гауссова распределения:

1) симметрично относительно <x>;

2) достигает максимального значения в точке <x>;

3) быстро стремится к нулю, когда | <x>-x | становится большим по сравнению с σ.

При измерениях физических величин часто приходится учитывать, что в разброс значений вносят свой вклад различные причины, которым соответствует одинаковый закон распределения. Центральная предельная теорема теории вероятности гласит: если существует последовательность и взаимозависимость случайных величин, имеющих одно и то же распределение плотности вероятности с конечным математическим ожидаемым и одинаковой дисперсией, то при n → ∞ распределение приближается к нормальному.

МЕТОДИКА ЭКСПЕРИМЕНТА

Изучение нормального распределения случайных величин проводится на механической модели, воспроизводящей картину случайных отклонений падающих частиц от среднего положения, в результате большого числа равновероятных актов рассеяния.

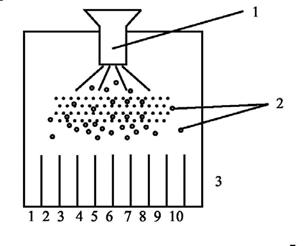
Рис. 4.

На рис. 4 приведена схема установки - доски Гальтона. Плоский вертикальный ящик с прозрачной передней стенкой имеет вверху воронку 1, в которую насыпается крупа 2. Под воронкой расположено несколько рядов иголок. Крупа при падении на иглы ударяется об них и рассеивается. Внизу находится приемная кювета 3, разделенная на вертикальные ячейки. Ширина всех ячеек одинакова. Все ячейки пронумерованы.. Крупа через воронку сыплется до тех пор, пока центральные ячейки приемной кюветы 3 не заполнятся почти доверху. Крупа насыпается равномерно.

Эксперимент проводится с малым и большим числом рассеивающих центров. В каждую i-ю ячейку, центр которой имеет координату

x_i= i - 0.5 (17)

в условных единицах, равных ширине ячейки, попадают крупинки, отклоняющиеся от вертикали на величину, лежащую в единичном интервале вблизи значения:

D x_i = x_i - <x>, (18)

где <х> - координата центра распределения (среднее значение х).

Высота заполнения i-й ячейки y_i пропорциональна вероятности отклонения шарика на величину Δx_i (т.е. числу частиц, испытавших такие отклонения).

Результаты измерений нормируются:

(19)

где Y_i - нормированный результат;

y_i - высота заполнения i-й ячейки;

- сумма всех y_i ;

f(x_i) - плотность распределения.

Среднее значение <x>, дисперсия, стандартное отклонение определяются по формулам:

<x>=∑x_iY_i, (20)

D = ∑(x_i-<x>)²Y_i, (21)

(22)

В данной лабораторной работе используются два вида крупы (пшено и гречка), поэтому выполнятся два независимых эксперимента. В работе также моделируется эксперимент с малым и большим числом рассеивающих центров. Для этого убираются иголки из четных ячеек (по горизонтали) и через ряд по вертикали.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Установите иглы так, чтобы их число было максимально.

2. Заготовьте таблицу результатов измерений 1 и 2.

Таблица 1.

i	x_i	y_i	Y_i	x_iY_i	<x>

… .

Таблица 2.

x_i	x_i - <x>	(x_i - <x>)²	(x_i - <x>)²Y_i	D	σ

3. Вставьте воронку в боковое отверстие на доске Гальтона. Насыпьте через воронку крупу в приемную кювету. Измерьте уровень крупы в каждой ячейке. Занесите в табл. 1 и 2 результаты измерений и расчетов, используя формулы (19-22).

4. Представьте результаты измерений табл.1 в виде гистограммы (х_i -координата i-ой ячейки, у _i - уровень крупы в i-ой ячейке, ширина всех ячеек одинакова).

5. По результатам измерений постройте экспериментальную кривую Y(x). Ось абсцисс - x_i; ось ординат - Y_i.

6. Рассчитайте и постройте теоретическую кривую f(x) в соответствии с формулой (13).

7. Сравните экспериментальную и теоретическую кривые. Сделайте
соответствующие выводы.

8. Измените число рассеивающих центров, как указано в методике.

9. Выполните пункты 2 - 9 с новым числом рассеивающих центров. Сделайте соответствующие выводы.

10. Возьмите другую крупу. Выполните пункты (2 - 9) для новой
крупы.

ВНИМАНИЕ! Гистограмма, экспериментальная и теоретическая кривые должны быть представлены на одном графике!

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое случайная величина? Среднее арифметическое?
Стандартное отклонение? Дисперсия?

2. Что такое гистограмма? Как она строится?

3. Какие законы моделируются в данной работе?Какое распределение называется нормальным? биномиальным?

4. Что такое функция плотности вероятности f(x)? Каковы ее свойства?

5. Как вычислить вероятность попадания результата в конечный интервал? Что это означает? Ответ поясните графически.

ЛИТЕРАТУРА

[I]§§ 70, 73;

[3] § 6;

[4] §§ 8,9;

[5] 1.5; [II]стр. 14-32.

ЛАБОРАТОРНАЯ РАБОТА № 2-02.

Дата добавления: 2019-02-12; просмотров: 212; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!