Городская математическая олимпиада (2009 год)

 

Условия задач

 

8 класс

1. Иван Петрович в 13 раз старше своей дочери. Три года назад он был в 6 раз старше своего сына. Сколько лет Ивану Петровичу и его детям?

2. В прямоугольном треугольнике один из углов равен 30°. Докажите, что в этом треугольнике отрезок перпендикуляра, проведенного через середину гипотенузы до пересечения с катетом втрое меньше этого катета.

3. Несколько чисел выписаны по кругу. Известно, что их сумма положительна. Докажите, что найдутся два рядом стоящих числа с положительной суммой. Будет ли справедливо это утверждение, если числа записаны в ряд?

4. Назовем натуральное число "замечательным", если оно - самое маленькое среди всех натуральных чисел с такой же, как у него, суммой цифр. Сколько существует трехзначных замечательных чисел?

5. Шестизначное число, все цифры которого различны, делится на 37. Доказать, что из тех же цифр можно составить другое число, которое также делится на 37.

 

9 класс

1. Решить уравнение x⁶ + x⁴ – 2x³ - 4x + 5 = 0.

2. Докажите, что среди 18 последовательных трехзначных чисел найдется хотя бы одно, которое делится на сумму своих цифр.

3. Несколько чисел выписаны по кругу. Известно, что их сумма положительна. Докажите, что найдутся два рядом стоящих числа с положительной суммой. Будет ли справедливо это утверждение, если числа записаны в ряд?

4. В футбольном турнире участвовало 10 команд. Известно, что у каждой команды число побед оказалось равным числу ничьих. Сколько всего матчей закончилось вничью, если каждые две команды сыграли между собой 1 раз?

5. Внутри правильного треугольника АВС лежит точка О. Известно, что ÐАОВ=113°, ÐВОС=123°. Найти углы треугольника, стороны которого равны отрезкам ОА, ОВ и ОС.

 

10 класс

1. Найдите такую функцию f(x), что f(x + 2) = x² + 2x + 7.

2. К двум окружностям, пересекающимся в точках М и К проведена общая касательная (А и В – точки касания). Докажите, что ÐАМВ + ÐАКВ =180°.

3. Решить уравнение .

4. Написано 2009 натуральных чисел. Доказать, что можно зачеркнуть одно число так, чтобы произведение оставшихся чисел можно было представить в виде разности квадратов двух целых чисел.

5. Тридцать студентов с пяти курсов придумали 40 задач для олимпиады, причем однокурсники - одинаковое количество задач, а студенты с разных курсов - разное. Сколько студентов придумали по одной задаче?

11 класс

1. Найдите такую функцию f(x), что f(x + 2) = x² + 2x + 7.

2. Доказать, что ни для каких чисел x, y, z не могут одновременно выполняться 3 неравенства: ïxï<ïy–zï, ïyï<ïz–xï, ïzï<ïx–yï.

3. Доказать, что при любом а уравнение a²cos⁸x – 2acos⁶x + 2cos2x = 0 имеет решение.

4. Из двух треугольных пирамид с общим основанием одна лежит внутри другой. Может ли сумма ребер внутренней пирамиды быть больше суммы ребер внешней?

5. Пусть x₁, x₂, x₃, … - монотонно возрастающая последовательность натуральных чисел, удовлетворяющая соотношению: член последовательности с номером x_n равен 3n для любого n. Найдите а) x₁; б) x₁₀₀.

Решения.

 

8 класс

1. Пусть дочери Ивана Петровича x лет, а сыну 3 года назад было y лет. Тогда возраст Ивана Петровича равен 13x = 6y+3. Из этого соотношения следует, что x делится на 3. С другой сторон, 6y = 13x – 3, а потому x должно быть нечетным числом. Так что x = 3 (если x=9, то Ивану Петровичу 117 лет, а в России таких долгожителей нет). В этом случае y=6, значит, сейчас сыну Ивана Петровича 9 лет, а самому Ивану Петровичу 39 лет.

2. Пусть АВС – данный треугольник (угол С – прямой, ÐВ=30°), точка К – середина гипотенузы, точка М – точка пересечения перпендикуляра с катетом ВС. Тогда в треугольнике АМС отрезок МК является высотой и медианой, то есть этот треугольник равнобедренный. Отсюда следует, что ÐМАК=ÐВ=30° и ÐМАС=60°-30°=30°. Тогда АМ = 2МС. Учитывая, что ВМ=АМ и ВМ=2МК, получим, что ВС=3МК.

3. Если общее количество чисел четно, то разобьем их на пары рядом стоящих чисел. Очевидно, что в какой-то паре сумма чисел должна быть положительной. Если общее количество чисел нечетно, то выберем отрицательное число, а остальные числа вновь разобьем на пары и выберем пару с положительной суммой. Если среди данных чисел нет отрицательного, то возьмем положительное число и любое стоящее рядом с ним. Для чисел, записанных в ряд, утверждение неверно. В качестве примера можно взять числа 2, -3, 2.

4. "Замечательными" являются трехзначные числа, сумма цифр которых находится в границах от 19 до 27 (меньшую сумму цифр могут иметь двузначные или однозначные числа). Следовательно, трехзначных "замечательных" чисел — девять.

5. Пусть  - данное число. Докажем, что число также делится на 37. . Однако 999 делится на 37, а потому  тоже делится на 37.

 

9 класс

1. Заметим, что x⁶ + x⁴ – 2x³ - 4x + 5 = (x³-1)²+(x²-2)². Это выражение равняется 0 только в том случае, если оба слагаемых равны 0. Однако x³-1 и x²-2 не могут одновременно обращаться в 0. Значит, уравнение не имеет решения.

2. Среди 18 последовательных натуральных чисел имеется два, которые делятся на 9, причем одно из них четное, то есть это число делится на 18. С другой стороны, сумма цифр каждого из этих чисел также должна делиться на 9, а, значит, эта сумма будет равняться 9 или 18. Единственным исключением будет число 999, но это число делится на сумму своих цифр.

3. Смотрите решение задачи 3 для 8 классов.

4. Пусть x - число матчей, закончившихся вничью, y – число матчей, закончившихся результативно. Если сложить количество ничьих у каждой команды, мы получим 2х, так как вничью играют две команды. Если сложить количество побед у каждой команды, мы получим у, так как в закончившемся результативно матче выигрывает лишь одна команда. По условию задачи имеем 2х=у, то есть вничью закончилась треть всех матчей. Так как всего в турнире было проведено 45 матчей, то 15 из них закончились вничью.

5. Решение. Построим за пределами треугольника АВС точку Р таким образом, что ВР = ВО, СР = АО. Так как треугольники ВРС и ВОА равны, то ÐРВС=ÐАВО, поэтому ÐОВР=60°, то есть треугольник ВОР равносторонний и ОР=ОВ. Таким образом, стороны треугольника РОС равны отрезкам ОА, ОВ и ОС. При этом ÐОРС=ÐВРС - 60°=ÐАОВ - 60°= 53°; ÐРОС=ÐВОС - 60°= 63°; ÐРСО = 64°.

 

10 класс

1. Обозначим x+2=t. Тогда x = t-2 и f(t) = (t-2)²+2(t-2)+7 = t²-2t+7. То есть f(x) = x²-2x+7.

2. Пусть точка М находится ближе к касательной АВ, чем точка К. Тогда ÐАМВ = 180° - ÐМАВ - ÐМВА, а ÐАКВ = ÐАКМ+ÐВКМ. Заметив, что ÐАКМ=ÐМАВ (они оба равны половине дуги АМ), а ÐВКМ= ÐМВА (они равны половине дуги ВМ), получим утверждение задачи.

3. Так как x≥0 и x-y+1≥0, то 2x-y+2 = x+x-y+1+1 ≥ 1, откуда . Равенство возможно только в том случае, когда все три слагаемых в левой части уравнения равны 0. То есть x=0, y=1.

4. В виде разности квадратов можно представить числа, которые можно задать как произведение двух нечетных чисел или как произведение двух четных. Если среди данных чисел лишь одно четное, вычеркнем его, в противном случае вычеркнем любое число таким образом, чтобы осталось, по меньшей мере, два четных. Далее очевидно.

5. Выберем пять студентов, по одному с каждого курса. Так как количество придуманных ими задач различно, то этими студентами придумано не менее, чем 1 + 2 + 3 + 4 + 5 = 15 задач. Тогда остальные 25 студентов придумали не более чем 40 - 15 = 25 задач. То есть каждый из них придумал по одной задаче, следовательно, всего по одной задаче придумали 26 человек.

11 класс

1. Смотрите решение задачи 1 для 10 класса.

2. Возведем обе части каждого неравенства в квадрат и, перенеся правую часть налево, применим формулу «разность квадратов». Мы получили три отрицательных числа. Значит, их произведение тоже будет отрицательно. Однако, с другой стороны, это произведение равно (x+z-y)²(x+y-z)²(y+z-x)², то есть отрицательным быть не может.

3. Преобразуем уравнение к виду a²cos⁸x – 2acos⁶x + 4cos²x - 2 = 0 и, сделав замену cos²x = t, 0≤t≤1, получим a²t⁴ – 2at³+ 4t – 2 = 0. При t=0 левая часть этого уравнения отрицательна, а при t=1 она равна a²-2a+2, то есть положительна при всех значениях а. Это означает, что при всех а исходное уравнение имеет решение.

4. Может. Пусть в пирамиде ТАВС ребра ТС, АС и ВС равны 1, а ребра АВ, ТА, ТВ равны х. Будем считать, что х значительно меньше 1. На ребре ТС возьмем точку Т₁ такую, что СТ₁=х. Уменьшая х, мы можем добиться, чтобы сумма ребер внутренней пирамиды (Т₁АВС) стала сколь угодно близкой к 4. В то же время сумма ребер внешней пирамиды будет сколь угодно близка к 3.

5. Допустим, что x₁=m, тогда x_m=3. Очевидно, что m ≠ 1. Если m≥3, то в силу монотонности последовательности x_m > x₁ ≥ 3 = x_m, что невозможно. Таким образом, x₁=2, x₂=3, x₃=6, x₆=9, x₉=18, x₁₈=27, x₂₇=54_, x₅₄=81, x₈₁=162. Заметим, что между x₂₇=54 и  x₅₄=81 расположено 26 членов последовательности, которые в силу монотонности, могут принимать ровно 26 различных значений 55, 56, 57, … 80. Очевидно, что x₂₈=55, x₂₉=56, … x₅₃=80. Но это значит, что x₅₅=84, x₅₆=87, … x₈₀=159. В частности x₆₀=99, x₆₁=102, а потому x₉₉=180, а x₁₀₂=183. В силу все той же монотонности x₁₀₀=181.

 

 

ОТКРЫТОЕ ПЕРВЕНСТВО 17 ШКОЛЫ

(городские олимпиады для 5-7 классов)

 

Олимпиада (2001 год)

 

5 класс

1. На доске выписаны цифры 12345. Поставьте между ними 2 знака умножения так, чтобы получившееся при этом произведение было наибольшим.

2. Автобусы проезжают мимо 17 школы с интервалом в 2 минуты. Сколько автобусов насчитал Петя во время урока математики, если последний автобус он увидел через 17 минут после того, как начал смотреть в окно?

3. Прямоугольник разрезали на 5 квадратов (не обязательно одинаковых). Каким образом могли это сделать? Укажите не менее трех способов.

4. В числе 12345678901234567890 зачеркните 10 цифр так, чтобы получившееся число было как можно больше.

5. Коза и корова съедают воз сена за 45 дней, корова и овца за 60 дней, а овца и коза ­– за 90 дней. За сколько дней съедят воз сена корова, коза и овца вместе?

Решения.

1. Два знака умножения можно расставить шестью способами. Произведение будет максимальным, если это сделать так: 123×4×5=2460.

2. 17, 15, 13, 11, 9, 7, 5, 3, 1 – всего 9 автобусов.

3. Из пяти квадратов прямоугольник можно составить разными способами. Вот некоторые из них:

4.

9234567890

5. Сосчитаем, сколько сена съедят две коровы, две козы и две овцы за 180 дней. Первая корова и первая коза съедят за это время 4 воза сена, вторая корова и первая овца – 3 воза сена, вторая коза и вторая овца – 2 воза сена. Всего получилось 9 возов. То есть за 20 дней две коровы, две козы и две овцы съедят один воз, а потому одна корова, одна коза и одна овца съедят один воз за 40 дней.

6 класс

1. Найдите наименьшее натуральное число, сумма цифр которого равна 29.

2. Дан клетчатый прямоугольник длиной 18 и шириной 8 клеток. Как разрезать его по границам клеток на две части, из которых потом можно сложить квадрат? Покажите на рисунках, как надо разрезать и как – складывать.

3. Отметьте 10 клеток доски 4´4 таким образом, чтобы в каждом горизонтальном и вертикальном ряду оказалось отмеченным четное число клеток.

4. Известно, что из четырех высказываний: 1) число А делится на 6; 2) число А делится на 8; 3) число А делится на 24; 4) число 32 делится на А – два верных и два неверных. Найдите все такие числа А.

5. Малыш может съесть торт за 10 минут, банку варенья за 8 минут и выпить кастрюлю молока за 15 минут. Карлсон то же самое может сделать за 2, 3 и 4 минуты соответственно. За какое время они вместе съедят торт, банку варенья и выпьют кастрюлю молока?

 

Решения.

1. Это число 2999. Если взять более маленькое число, то в нем хотя бы одна цифра меньше, чем в этом, и нет ни одной цифры больше, чем в числе 2999. А потому и сумма цифр в любом меньшем числе меньше 29.

2.

 

 

3. Это можно сделать, например, так:

4. Если верно третье высказывание, то верны также первое и второе, то есть верны три высказывания, что противоречит условию. Первое и второе условия не могут быть верны одновременно, так как тогда верно и третье. По той же причине оба этих условия не могут быть одновременно ложными. Значит, либо первое утверждение верно, а второе нет, либо наоборот. Кроме того, истинным является и четвертое высказывание. Но первое и четвертое высказывание противоречат друг другу. Значит, истинными являются второе и четвертое высказывания. То есть А может равняться 8, 16 и 32.

5. Малыш ест торт в пять раз медленнее Карлсона, варенье в 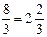 раза медленнее и пьет молоко в  раза медленнее. То есть торт, варенье и молоко будут съедены быстрее всего в том случае, если малыш примется за варенье. Пока Карлсон ест торт и пьет молоко, пройдет 6 минут, и малыш съест  варенья, оставшуюся четверть варенья они съедят вместе за  минуты (чтобы определить это, мы должны решить задачу на совместную работу).

7 класс

1. Точки А(4;11) и В(41;52) лежат на графике линейной функции. Укажите на этом графике еще несколько точек с целочисленными координатами.

2. Пятачок и Винни-Пух одновременно отправились в гости друг к другу. Так как всю дорогу они считали галок, то не заметили друг друга при встрече. После встречи Пятачок подошел к дому Винни-Пуха через 4 минуты, а Винни-Пух к дому Пятачка – через 1 минуту. Во сколько раз скорость Винни-Пуха больше скорости Пятачка?

3. Какое число больше: 888…88×333…33 или 444…44×666…66 (каждый сомножитель является 100-значным числом)?

4. Среди всех треугольников, у которых сумма медиан равна данному числу, укажите треугольник, имеющий наибольшую сумму высот.

5. Первая цифра десятичного числа равна числу единиц в записи этого числа, вторая цифра – числу двоек, третья – числу троек, … , десятая – числу нулей. Найдите это число.

 

Решения.

1. Мы видим, что при увеличении аргумента на 37 функция увеличилась на 41. Значит, при увеличении аргумента на 74 функция увеличится на 82, при увеличении аргумента на 111 функция увеличится на 123 и так далее. Отсюда найдем точки с целочисленными координатами: В(78; 93), С(115; 134) и так далее.

2. Пусть скорость Винни в k раз больше скорости Пятачка. Тогда расстояние, пройденное Винни-Пухом до встречи в k раз больше, чем расстояние, пройденное Пятачком. То есть после встречи Пятачку предстоит пройти в k  раз больше со скоростью, в k  раз меньшей. То есть на путь после встречи Пятачок затратит в k² больше времени. Из условия видно, что k²=4,  то есть k = 2.

3. Первый множитель первого произведения в два раза больше, чем первый множитель второго произведения, а второй множитель первого произведения в два раза меньше. Поэтому данные произведения равны.

4. Каждая высота в треугольнике не больше медианы, проведенной из той же вершины. Поэтому сумма высот будет наибольшей в том случае, когда все высоты совпадают с медианами, то есть в случае равностороннего треугольника.

5. Это число 2100010006.

 

 

Олимпиада (2002 год)

 

5 класс

1. Решить числовой ребус: ЭЮ×Я=255 (разным буквам соответствуют разные цифры).

2. У Васи имеется десять карточек с цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, три карточки со знаком равенства и по одной карточке со знаками сложения, вычитания и умножения. Васе нужно составить из этих карточек три арифметических примера, причем он должен использовать все карточки. Как это можно сделать?

3.  7 рыжих и 6 черных тараканов съедают пирожное в два раза быстрее, чем 4 рыжих и 2 черных. Кто ест быстрее: черный таракан или рыжий?

4. Можно ли прямоугольную таблицу размером 5´4 заполнить натуральными числами так, что сумма чисел, стоящих в каждой строке и в каждом столбце будет равна 10?

5. Одна сторона прямоугольника вдвое длиннее другой. Как разделить его на 8 одинаковых частей, из которых можно сложить прямоугольник, у которого одна сторона в 4 раза длиннее другой?

 

Решения.

1. Число 255 можно разложить на множители несколькими способами: 255 = 51×5; 255 = 85×3; 255 = 17×15; 255 = 255×1. Так как в нашем примере двузначное число умножается на однозначное, причем для записи этих чисел использованы три разные цифры, то нам подходит только равенство 255 = 85×3.

2. Например, так: 7+1=8; 9–6=3; 5×4=20.

3. 8 рыжих тараканов и 4 черных съедают пирожное вдвое быстрее, чем 4 рыжих и 2 черных, то есть за такое же время, как 7 рыжих и 6 черных. Отсюда ясно, что замена одного рыжего таракана на двух черных не изменяет общей скорости поедания мороженого. То есть рыжий таракан ест вдвое быстрее черного.

4. Нельзя. Действительно, складывая все числа, стоящие в таблице, по строкам, мы получим 5×10 = 50. Складывая эти же числа по столбцам, получим 4×10 = 40.

5.

 

6 класс

1. Натуральное число умножили на сумму его цифр и получили в итоге 1000. Каким могло быть исходное число?

2. 7 рыжих и 6 черных тараканов съедают пирожное в два раза быстрее, чем 4 рыжих и 2 черных. Кто ест быстрее: черный таракан или рыжий?

3. В турнире по футболу участвовало 8 команд. После того, как каждая команда сыграла с каждой по 1 матчу, оказалось что эти команды набрали 15, 14, 13, 9, 8, 7, 4 и 3 очка. Известно, что за победу присуждается 3 очка, за ничью – 1 очко, за поражение – 0 очков. Сколько матчей в турнире закончилось вничью?

4. В написанном на доске примере на умножение хулиган Петя исправил две цифры, в результате чего пример стал выглядеть так: 4×5×4×5×4=2247. Восстановите исходный пример.

5. Вовочка раскрашивает клетчатую доску размером 8´8, соблюдая следующее правило: каждая следующая закрашенная клетка должна иметь общую сторону с предыдущей закрашенной клеткой, но не должна иметь общую сторону ни с одной другой из ранее закрашенных клеток. Вовочке удалось покрасить 36 клеток. Побейте его рекорд.

 

 

Решения.

1. Искомое число должно быть делителем числа 1000. Выпишем все эти делители: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000. Условию задачи удовлетворяют числа 125 и 1000.

2. Смотрите задачу 3 для 5 классов.

3. Всего было сыграно 28 матчей. Если бы все они закончились результативно, то общая сумма полученных командами очков равнялась бы 28×3=84. На самом же деле эта сумма равняется 73. Так как каждая ничья приносит командам два очка (1+1) вместо трех, то недостающий 11 очков являются результатом того, что 11 матчей закончились вничью.

4. В левой части примера 3 четных множителя. Даже если исправить два из них, все равно один четный множитель останется, то есть в правой части должно стоять четное число, а потому последняя цифра в нем должна быть исправлена. Но тогда в левой части можно исправить лишь одну цифру, поэтому наверняка останется один из множителей, равных 5. То есть в правой части стоит число, которое делится на 5. Так как это число к тому же четное, то оно должно оканчиваться цифрой 0. Получили пример 4×5×4×5×4=2240, в котором нужно исправить одну цифру. Возможны три варианта: в левой части все цифры остаются неизменными, в левой части меняется цифра 4, в левой части меняется цифра 5. Первый вариант не проходит, так как произведение цифр в левой части равно 1600, что отличается от правой части на три цифры. Рассмотрим второй вариант. Заменим цифру 4 на цифру х. Получим 4×5×4×5×х=2240, что невозможно, так как х должно быть цифрой. Разбирая точно так же третий вариант, получим, что цифру 5 надо заменить на цифру 7. Итак, пример должен выглядеть так: 4×5×4×7×4=2240.

5. Например, это можно сделать так:

 

13	14	15		37	38	39	40
12		16		36			41
11		17		35	34		42
10		18	19		33	32
9	8		20	21		31
	7	6		22		30	29
1		5		23			28
2	3	4		24	25	26	27

Числа, стоящие в клетках, показывают, в каком порядке эти клетки закрашиваются.

 

7 класс

1. В написанном на доске примере на умножение хулиган Петя исправил две цифры, в результате чего пример стал выглядеть так: 4×5×4×5×4=2247. Восстановите исходный пример.

2. Петя ходит в бассейн раз в три дня, Вова – раз в четыре дня, Вася – раз в пять дней. В понедельник они встретились в бассейне. Через сколько дней дети снова окажутся в бассейне вместе и какой это будет день недели?

3. Имеется 4 гири с надписями 1, 2, 3 и 4 грамма. Одна из гирь дефектная: ее вес отличается от числа, написанного на этой гире. Можно ли за два взвешивания на чашечных весах определить эту гирю и выяснить, легче она или тяжелее?

4. Вершину А треугольника АВС соединили отрезками с двумя точками, которые делят на три равные части сторону ВС. Могут ли эти отрезки делить на три равные части угол А?

5. Вовочка раскрашивает клетчатую доску размером 8´8, соблюдая следующее правило: каждая следующая закрашенная клетка должна иметь общую сторону с предыдущей закрашенной клеткой, но не должна иметь общую сторону ни с одной другой из ранее закрашенных клеток. Вовочке удалось покрасить 36 клеток. Побейте его рекорд.

 

Решения.

1. Смотрите задачу 4 для 6 классов.

2. Количество дней, через которое мальчики вновь окажутся в бассейне вместе, должно делиться на 3, 4 и 5. Минимальное натуральное число. обладающее этим свойством — 60. Таким образом. Мальчики встретятся через 8 недель и 4 дня. Легко видеть, что это будет пятница.

3. Пусть m₁, m₂, m₃, m₄ — истинные массы гирек с надписями 1, 2, 3 и 4 грамма соответственно. Сравним сперва m₁ + m₂ c m₃, а затем m₁ + m₃ с m₄. При этом возможны следующие варианты:

1) m₁ + m₂ > m₃, а m₁ + m₃ > m₄. Тогда m₁>1.

2) m₁ + m₂ > m₃, а m₁ + m₃ < m₄. Тогда m₃<3.

3) m₁ + m₂ < m₃, а m₁ + m₃ < m₄. Тогда m₁<1.

4) m₁ + m₂ < m₃, а m₁ + m₃ > m₄. Тогда m₃>3.

5) m₁ + m₂ = m₃, а m₁ + m₃ < m₄. Тогда m₄>4.

6) m₁ + m₂ = m₃, а m₁ + m₃ > m₄. Тогда m₄<4.

7) m₁ + m₂ > m₃, а m₁ + m₃ = m₄. Тогда m₂>2.

8) m₁ + m₂ < m₃, а m₁ + m₃ = m₄. Тогда m₂<2.

4. Нет, так как предположив противное, мы легко докажем, что оба эти отрезка должны быть перпендикулярны стороне ВС. При этом используется тот факт, что треугольник. В котором медиана совпадает с биссектрисой, является равнобедренным.

5. Смотрите задачу 5 для 6 классов.

 

 

Олимпиада (2003 год)

 

5 класс

1. В озере плавает яблоко:  его находится под водой, а  – над водой. К яблоку подлетает птичка и подплывает рыбка, которые одновременно начинают его есть, причем птичка делает это в два раза быстрее рыбки. Кто съест больше?

2. Тане не хватает 2 рублей для покупки 8 воздушных шариков. Если она купит 5 шариков, то у нее останется 10 рублей. Сколько стоит шарик?

3. Веревку сложили пополам, потом еще раз пополам и еще раз пополам. Сложенную таким образом веревку перерезали ножницами, в результате чего она распалась на несколько частей. Сколько всего получилось частей?

4. Винни Пух, Кролик, Пятачок и ослик Иа-Иа вместе съели 70 конфет, причем каждому досталась хотя бы одна конфета. Винни Пух съел больше Пятачка, Пятачок – больше Кролика, а вместе Пятачок и Кролик съели 45 конфет. Сколько конфет съел ослик?

5. Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток. Укажите три различных решения этой задачи.

 

Решения.

1. Птичка съест большую часть яблока, так как яблоко будет плавать до тех пор, пока его полностью не съедят.

2. 8 – 5 = 3 шарика стоят 2 + 10 = 12 рублей, то есть один шарик стоит 4 рубля.

3. Если веревку трижды сложить пополам, то она будет сложена в 2×2×2 = 8 слоев. Перерезав сложенную таким образом веревку ножницами, мы, следовательно, сделаем 8 разрезов. То есть веревка распадется на 9 частей.

4. Кто-то один из двоих – Пятачок или Кролик – съел не меньше 23 конфет, то есть Винни Пух съел не меньше 24 конфет. Так как 45  + 24 = 69, то ослик съел ровно одну конфету.

5.

 

6 класс

1. Веревку сложили пополам, потом еще раз пополам, еще раз пополам и еще раз пополам. Сложенную таким образом веревку перерезали ножницами, в результате чего она распалась на несколько частей. Сколько всего получилось частей?

2. Даны два числа. 60% первого числа составляют 80% от числа, составляющего 70% второго числа. Какое из чисел больше?

3. Дед Мороз, собирая подарки, обнаружил, что если в каждый подарок класть по 15 конфет вместо 13, то имеющихся у него конфет хватит на такое же количество подарков. Какое наибольшее количество конфет могло быть у Деда Мороза?

4. На доске написано число 469. За один ход разрешается либо удваивать число, либо стирать его последнюю цифру. Можно ли за несколько ходов получить число 14?

5. Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток. Укажите четыре различных решения этой задачи.

 

Решения.

1. Если веревку четыре раза сложить пополам, то она будет сложена в 2×2×2×2 = 16 слоев. Перерезав сложенную таким образом веревку ножницами, мы, следовательно, сделаем 16 разрезов. То есть веревка распадется на 17 частей.

2. 80% от числа, составляющего 70% второго числа – это 56% второго числа. Таким образом, 60% первого числа равны 56% второго числа. То есть второе число больше.

3. Пусть Дед Мороз собирает х подарков. Если он будет класть в каждый подарок на 2 конфеты больше, то ему понадобится для этого 2х конфет. Эти 2х конфет не составляют целого подарка, таким образом, максимальное значение числа х равно 6. В этом случае у Деда Мороза должно быть 90 конфет.

4. 469 – 46 – 92 – 9 – 18 – 36 – 72 – 144 – 14

5. Смотрите решение задачи 5 для 5 класса.

 

7 класс

1. Может ли число 23021³⁷⁷ – 1 быть простым?

2. Дед Мороз, собирая подарки, обнаружил, что если в каждый подарок класть по 15 конфет вместо 13, то имеющихся у него конфет хватит на такое же количество подарков. Какое наибольшее количество конфет могло быть у Деда Мороза?

3. Веревку сложили пополам, потом еще раз пополам, а потом еще раз пополам. Сложенную таким образом веревку перерезали ножницами, в результате чего она распалась на несколько частей. Среди них самая короткая имела длину 5 см, а самая длинная – 16 см. Какая длина была у исходной веревки?

4. В семье 4 человека. Если Маше удвоят стипендию, то общий доход всей семьи возрастет на 5%; если вместо этого маме удвоят зарплату, то общий доход возрастет на 25%; если же зарплату удвоят папе, то на 40%. На сколько процентов возрастет общий доход семьи, если дедушке удвоят пенсию?

5. Прямоугольник разрезали тремя вертикальными и тремя горизонтальными разрезами на 16 прямоугольников разных размеров. Оказалось, что периметр каждого из получившихся прямоугольников составляет целое число метров. Обязательно ли периметр исходного прямоугольника – целое число метров?

 

Решения.

1. Число 23021³⁷⁷ оканчивается на единицу, поэтому число 23021³⁷⁷ – 1 оканчивается на 0, то есть делится на 10 и не является простым.

2. Смотрите решение задачи 3 для 6 класса.

3. Если сложенная три раза пополам веревка разрезается на части длиной х и у, то исходная веревка распадется на куски длиной х, 2х и 2у (или у, 2у и 2х). Если меньший кусок веревки имеет длину х, то х = 5, у = 8, а длина исходной веревки равна 8(х + у) = 104см. Если меньший кусок имеет длину 2у, то у = 2,5; х = 8, а длина веревки равна 8(х + у) = 84см.

4. Из условия задачи следует, что Машина стипендия, мамина и папина зарплаты составляют соответственно 5%, 25% и 40% семейного бюджета. Таким образом дедушкина пенсия составляет 30% семейного бюджета и, если пенсию удвоят, то бюджет возрастет на 30%.

5. Периметр исходного прямоугольника равен сумме периметров выделенных прямоугольников, то есть является целым числом.

 

 

Олимпиада (2004)

 

5 класс.

1. Детей выстроили в ряд. Вовочка стоит пятым слева, а Маша стоит седьмой справа. Сколько всего детей, если Маша стоит рядом с Вовочкой слева от него?

2. Три гусенка и четыре утенка весят 2кг 500 граммов, а четыре утенка и 3 гусенка весят 2кг 400 граммов. Сколько весит гусенок?

3. Можно ли квадрат разрезать на 6 квадратов меньшего размера (не обязательно одинаковых)?

4. Учительница написала на доске два числа. Вовочка сначала их перемножил и получил ответ 32, а потом сложил и получил ответ 15. Найти эти числа, если известно, что в каждом действии Вовочка ошибся ровно на 1.

5. На окраску деревянного кубика ушло 108 граммов краски. Когда краска высохла, кубик распилили на 27 одинаковых кубиков. Сколько краски потребуется, чтобы покрасить образовавшиеся при этом неокрашенные поверхности?

 

Решения.

1. Всего в ряду стоит 10 детей, слева от Маши трое, справа от Вовочки пятеро:    · · · М В · · · · ·

2.

7 гусят и 7 утят весят 4кг 900г, поэтому 1 гусенок и 1 утенок весят 700г, 3 гусенка и 3 утенка – 2кг 100г. Теперь понятно, что гусенок весит 300г, а утенок 400г.

3. Можно:

4. Правильное произведение чисел может равняться либо 31, либо 33. В первом случае это могут быть только числа 31 и 1, а во втором – 3 и 11, а также 33 и 1. 31+1 = 32; 33+1 = 34; 11+3 =14. Только последняя сумма удовлетворяет условию задачи. Таким образом, искомые числа 11 и 3.

5. Чтобы разрезать куб на 27 кубиков, нужно сделать 6 разрезов. После каждого разреза образуются две квадрата, равные по размерам граням куба. Всего надо будет покрасить 12 таких квадратов (разбитых на маленькие квадратики), то есть в два раза больше, чем имеется граней у куба. На покраску этих квадратов потребуется в два раза больше краски, чем ушло на покраску поверхности куба, то есть 216 граммов.

 

6 класс.

1. Килограмм мяса без костей стоит 120 рублей, килограмм мяса с костями – 102 рубля, а килограмм костей – 24 рубля. Сколько костей в килограмме мяса?

2. Длину прямоугольника увеличили на 30%, а ширину уменьшили на 30%. На сколько процентов изменилась площадь прямоугольника?

3. Учительница написала на доске два числа. Вовочка сначала их перемножил и получил ответ 32, а потом сложил и получил ответ 15. Найти эти числа, если известно, что в каждом действии Вовочка ошибся ровно на 1.

4. Как с помощью 11-литровой и 7-литровой бутыли набрать 2 литра воды из водопроводного крана?

5. Покажите, как разрезать прямоугольник размером 1х5 на пять частей и сложить из них квадрат.

 

Решения.

1. Пусть в килограмме мяса с костями х кг костей и (1–х)кг мяса. Тогда 24х + 120(1–х) = 102 или 96х = 18. Откуда находим х = (кг).

2. Пусть х – исходная длина прямоугольника, а у – его исходная ширина. Тогда после изменения размеров длина прямоугольника стала 1,3х, а ширина, 0,7у. То есть его площадь стала равна 1,3×0,7у = 0,91ху. То есть площадь прямоугольника уменьшилась на 9%.

3. См. решение задачи 4 для 5 класса.

4. Приведем последовательность переливаний:(11, 0) – (4, 7) – (4,0) – (0, 4) – (11,4) – (8, 7) – (8,0) – (1, 7) – (1, 0) – (0, 1) – (11, 1) – (5, 7) – (5,0) – (0,5) – (11, 5) – (9, 7) – (9,0) – (2, 7). В каждой паре чисел первое число означает количество воды в 11-литровой банке, а второе – в 7-литровой.

5.

 

7 класс.

 

1. Найти все натуральные числа, у которых наибольший делитель (не совпадающий с самим числом) равен 35.

2. Как с помощью 11-литровой и 7-литровой бутыли набрать 2 литра воды из водопроводного крана?

3. Вася и Петя составляли слова из букв слова МАТЕМАТИКА. Вася составил 17 слов, а Петя – 21 слово. После этого они зачеркнули совпадающие слова и сосчитали оставшиеся. Оказалось, что осталось 16 слов. Сколько всего различных слов придумали Вася и Петя вместе?

4. По дороге с одинаковыми скоростями в одном направлении движутся две автомашины. В 12 часов первая машина находилась в два раза дальше от поста ГИБДД, чем вторая. В 13 часов снова первая машина оказалась в два раза дальше от поста ГИБДД, чем вторая. В какое время вторая машина проехала мимо поста ГИБДД?

5. В треугольнике АВС проведены биссектрисы АМ и СК, пересекающиеся в точке О. Может ли угол АОС оказаться острым?

 

Решения.

1. Очевидно, что такие числа имеют вид 35р, где р – простое число, не превышающее 5. Таким образом, р может равняться 2, 3 или 5, а сами числа – 70, 105 и 175.

2. Последовательность переливаний задается следующей таблицей, где в первой строчке указано количество воды в 11-литровой бутыли, а во второй строчке – в 7-литровой.

0	7	7	11	0	3	3	10	10	11	0	6	6	11
7	0	7	3	3	0	7	0	7	6	6	0	7	2

3. Пускай было зачеркнуто 2x слов (x у Васи, x у Пети). Тогда 16+2x =17+21, то есть  x=11. Значит, всего было составлено 16+11=27 различных слов.

4. Пусть в 12 часов машины находились на расстоянии 2х и х от поста ГАИ по одну сторону от поста, а в 13 часов – на расстоянии 2у и у от поста, причем первая машина поста еще не достигла. Тогда за час первая машина проехала расстояние 2х–2у, а вторая – расстояние х+у. Так как скорости у машин одинаковые, то 2х–2у=х+у, откуда х=3у и скорость машин равна х+у=4у. В 12 часов вторая машина находилась на расстоянии х=3у от поста, поэтому она доехала до него за 45 минут.

Возможно, однако, что в 12 часов машины находились по разные стороны от поста ГАИ, а в 13 часов они оказались уже по одну стороны. В этом случае все происходит так же, как и в первом, только в обратном порядке. А потому вторая машина достигнет поста ГАИ через 15 минут.

5. ÐАОС = 360°–ÐВКО–ÐВМО–ÐВ. Так как ÐВКО = ÐА+0,5ÐС, а ÐВМО=ÐС+0,5ÐА, то нетрудно сосчитать, что ÐАОС = 180°–0,5ÐА–0,5ÐС, что больше 90°, так как ÐС+ÐА<180°.

Олимпиада (2005 год)

 

5 класс

1. Сколько было бревен, если, сделав 33 распила, получили 44 полена?

2. Можно ли расставить числа от 1 до 7 по кругу так, чтобы любое из них делилось на разность своих соседей?

3. В полдень Баба Яга вылетела на метле из Тридевятого царства и прибыла в Тридесятое царство в 14 часов местного времени. В полночь по местному времени она полетела обратно и вернулась в Тридевятое царство в шесть утра. Сколько времени длился полет в одну сторону?

4. Какое максимальное число шестиклеточных

 скобок можно разместить в квадрате 10х10?

5. Придумать 4 таких различных натуральных числа, что сумма обратных к ним величин равна 1.

Решения

1. После каждого распила число «кусков дерева» увеличивается на 1. Так как после 33 распилов их стало 44, то первоначально их было 44–33 = 11.

2. Можно, например 1562734.

3. В тридевятом царстве Баба Яга отсутствовала 12+6 = 18 часов. В тридесятом царстве она находилась 24–14 = 10 часов. Значит, в дороге она провела 18 – 10 = 8 часов. То есть дорога в один конец занимает 8:2 = 4 часа.

4. 16, например это можно сделать так:

1	1	6	6	6	6	7	7	7	7
1	5	6		5	6	7	8	8	7
1	5	5	5	5	15	15	8	9	9
1	1	14	14	14	14	15	8		9
2	2	14	13	13	14	15	8	8	9
2	4	4	13	16	15	15	16	9	9
2		4	13	16	16	16	16	10	10
2	2	4	13	13	11	11	11	11	10
3	4	4	3	12	11		12	11	10
3	3	3	3	12	12	12	12	10	10

Здесь одинаковыми цифрами отмечены клетки, принадлежащие одной скобочке.

5.

 

6 класс

1. Докажите, что число 1×3×5×…×2003+2×4×6×…×2004 делится на 991.

2. Отец и сын катались по кругу на катке, причем отец время от времени обгонял сына. Когда они стали кататься навстречу друг другу, то стали встречаться в пять раз чаще. Во сколько раз скорость отца больше скорости сына?

3. Может ли целое число при зачеркивании первой цифры уменьшиться в 57 раз?

4. Фигура составлена из квадратов.

Найти сторону левого нижнего квадрата,

если сторона самого маленького равна 1.

5. Учитель записал на доске 4 числа. Затем

каждый из 6 учеников выбрал из этих чисел

2 числа и сложил их. Затем учитель стер

свои числа и сумму, найденную Вовочкой.

На доске остались пять сумм: 13, 15, 16, 20 и 22.

Найти стертую сумму.

 

Решения.

1. Первое слагаемое делится на 991, потому что один из множителей в нем равен 991, а второе слагаемое делится на 991, так как один из множителей в нем равен 1982=991·2. Значит, вся сумма делится на 991.

2. Пусть х – скорость отца, а у – скорость сына. Из условия задачи следует, что х+у = 5(х–у), откуда х =1,5у.

3. Да, например число 7125. Чтобы придумать пример, надо рассмотреть уравнение 57x = x+10ⁿy , где у – первая цифра искомого числа, а х – число, получаемое из искомого зачеркиванием первой цифры. Из этого уравнения следует, что 7 – единственно возможное значение у. Поэтому 8x = 10ⁿ. Одним из решений этого уравнения как раз и будут числа x=125, n=3.

4. Пусть х – сторона левого нижнего квадрата (и квадрата, расположенного рядом). Тогда правый нижний квадрат имеет сторону х+1, правый верхний – сторону х+2, левый верхний – сторону х+3. А теперь получим уравнение 2х=(х+3)+1, откуда х=4.

5. Всего из 4 чисел можно получить 6 сумм, обладающих свойством: если расположить эти суммы в порядке возрастания (s₁, s₂, s₃, s₄, s₅, s₆), то s₁+s₆= s₂+s₅= s₃+s₄. Обозначим теперь неизвестную сумму за х. Возможны следующие случаи: x<13; 13<x<15 и т.д. В первом случае должны выполняться соотношения х+22=13+20=15+16. Так как второе из этих равенств неверно, то этот случай мы отбросим. Перебирая подобным образом случай за случаем, мы получим единственное решение: х=19.

 

 

7 класс

1. Имеется угольник с углом 70°. Как с его помощью построить угол 10°?

2. Среди натуральных чисел от 1 до 99 выбрали 50 чисел так, что никакие два из них не дают в сумме ни 99, ни 100. Какие числа выбраны? Ответ обосновать.

3. Отец и сын катались по кругу на катке, причем отец время от времени обгонял сына. Когда они стали кататься навстречу друг другу, то стали встречаться в пять раз чаще. Во сколько раз скорость отца больше скорости сына?

4. Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 13?

5. Учитель записал на доске 4 числа. Затем каждый из 6 учеников выбрал из этих чисел 2 числа и сложил их. Затем учитель стер свои числа и сумму, найденную Вовочкой. На доске остались пять сумм: 13, 15, 16, 20 и 22. Найти стертую сумму.

 

Решения.

1. Построим один за другим углы AOB, BOC, COD, DOE и EOF, равные 70°. Тогда ÐAOF=10°.

2. Рассмотрим пары чисел: 1 и 99, 2 и 98, 3 и 97 и т.д. Очевидно, что из каждой пары могло быть выбрано только по 1 числу. Так как пар всего 49, то пятидесятым числом является число 50, оставшееся без пары. Но тогда не могло быть выбрано число 49 (49+50=99), а потому было выбрано число 51 (иначе не наберется 50 чисел). Раз было выбрано число 51, то не могло быть выбрано число 48, а, значит, было выбрано число 52. Рассуждая и дальше подобным образом, мы придем к выводу, что были выбраны числа 50, 51, 52, … 99.

3. Смотрите решение задачи 2 для 6 классов.

4. Да. Например, 48999 и 49000.

5. Смотрите решение задачи 5 для 6 классов.

 

 

Олимпиада (2006 год)

 

5 класс

1. Найти наибольшее пятизначное число, у которого четвертая цифра больше пятой, третья цифра больше суммы четвертой и пятой, вторая больше суммы третьей, четвертой и пятой, а первая цифра больше суммы всех остальных.

2. Докажите, что из трех целых чисел всегда можно выбрать два, сумма которых делится на 2.

3. Веревочку сложили пополам, потом еще раз пополам и еще раз пополам (всего три раза). Потом полученную веревочку разрезали пополам. Сколько кусочков получилось?

4. Петя, Миша, Боря и Вова сыграли несколько партий в шахматы. Петя сыграл 5 партий, Миша – 6, Боря – 7, а Вова – 8. Сколько всего партий было сыграно.

5. Как прямоугольник длиной 16 см а шириной 9 см разрезать на две равные части, из которых можно составить квадрат?

 

Решения

1. 95210

2. Из трех чисел всегда можно выбрать либо два четных, либо два нечетных числа. Их сумма будет четным числом.

3. Всего было произведено 8 разрезов, то есть получилось 9 кусочков.

4. Всего было сыграно (5+6+7+8):2 = 13 партий.

5.

 

 

6 класс

1. Миша, Боря и Вова сыграли несколько партий в шахматы. Миша сыграл 5 партий, Боря – 7, а Вова – 8. Сколько партий сыграли между собой Вова и Боря.

2. Веревочку сложили пополам, потом еще раз пополам, еще раз пополам и еще раз пополам (всего 4 раза). Потом полученную веревочку разрезали пополам. Сколько кусочков получилось?

3. В аквариуме размером 2х2х1 плавает золотая рыбка. Если смотреть на аквариум спереди, то путь рыбки изображается линией на рисунке 1. Если смотреть справа, - линией на рисунке 2. Нарисуйте вид сверху.

4. В магазине имеются на равную сумму конфеты по 20 рублей за килограмм и конфеты по 30 рублей за килограмм. По какой цене следует продавать смесь этих конфет?

5. Можно ли из первых 50 натуральных чисел выбрать 36 чисел так, чтобы их сумма равнялась сумме 14 оставшихся чисел?

 

Решения

1. Всего они сыграли (5+7+8):2 = 10 партий. Так как Миша сыграл 5 партий, то Боря и Вова между собой сыграли 10 – 5 = 5 партий.

2. Всего было произведено 16 разрезов, то есть получилось 17 кусочков.

3.

 

4. Возьмем конфет каждого сорта на 60 рублей. Тогда 1 сорта их будет 3 кг, а второго сорта – 2 кг, всего 5 кг на 120 рублей. Значит, продавать их следует по 24 рубля за килограмм.

5. Нет, так как сумма первых пятидесяти натуральных чисел – нечетное число.

 

 

7 класс

1. В магазине имеются на равную сумму конфеты по 20 рублей за килограмм и конфеты по 30 рублей за килограмм. По какой цене следует продавать смесь этих конфет?

2. Через одну точку проведены три прямые. Угол между первой и второй прямыми равен 50°, а между второй и третьей – 70°. Найти угол между первой и третьей прямыми.

3. Футбольный мяч сшит из 32 лоскутов: белых шестиугольников и черных пятиугольников. Каждый черный лоскут граничит только с белыми, а каждый белый – с тремя черными и тремя белыми. Сколько лоскутов белого цвета, если границей между двумя лоскутами является их общая сторона.

4. Сумма цифр числа х равна у, а сумма цифр числа у равна z. Известно, что x+y+z =60. Найти х.

5. Докажите, что из семи целых чисел всегда можно выбрать три, сумма которых делится на 3. Верно ли это утверждение для 5 чисел?

 

Решения

1. Смотрите задачу 4 для 6 класса

2. Возможны два случая: 1) 70°–50°=20°; 2) 50°+70°=120° - тупой угол, поэтому угол между прямыми равен 180°– 120°=60°.

3. Пусть имеется х белых и у черных лоскутов. Тогда черные лоскуты имеют 5у общих отрезков с белыми, а белые 3х общих отрезков с черными. Очевидно, что 3х = 5у. В то же время х+у=32, откуда х=20, у=12.

4. Пусть х=10a+b. Тогда y=a+b. Если у – однозначное число, то z=a+b и 12a+3b=60 или 4a+b=20, откуда следует, что b делится на 4. Возможны 3 случая: b=0, a=5; b=4, a=4; b=8, a=3. Последний случай не подходит, т.к. a+b – двузначное. Если у – двузначное число, то z=a+b–9 и 12a+3b–9=60 или 4a+b = 23. Перебором находим b=7, a=4. Ответ: 47, 44, 50.

5. Из семи чисел всегда найдутся 3, дающие при делении на 3 одинаковые остатки. Их сумма делится на 3. Если из 5 чисел не удастся выбрать 3, имеющие при делении на 3 одинаковые остатки, то найдутся такие 3 числа, что все они имеют при делении на 3 разные остатки. Их сумма делится на 3.

 

Олимпиада (2007 год)

 

Класс

1. Из цифр 1, 2, 3, и 4 составить два числа, произведение которых минимально.

2. Можно ли квадрат разрезать на 6 квадратов меньшего размера (не обязательно одинаковых)?

3. На двух кустах сидело 25 воробьев. После того как с первого куста перелетело на второй 5, а со второго улетело 7 воробьев, то на первом кусте осталось вдвое больше воробьев, чем на втором. Сколько воробьев было на каждом кусте первоначально?

4. Золотоискатель Джек добыл 9 кг песка. Сможет ли он за три взвешивания отмерить 2 кг песка с помощью чашечных весов с двумя гирями – 200 г и 100г?

5. Заменить звездочки цифрами так, чтобы получилось верное равенство: *** • 9* = *2**. Найти все решения. Первые звездочки в числах заменяются на цифры, отличные от нуля.

Решения.

1. 1·234=234. Задача решается перебором вариантов.

2. Можно. Например, квадрат 3х3 легко разрезать на 1 квадрат размером 2х2 и 5 квадратов размером 1х1.

3. После того, как улетело 7 воробьев, на кустах осталось 18 воробьев, из них 12 на первом кусте, а 6 на втором. Таким образом, первоначально на первом кусте было 12+5=17 воробьев, а на втором 6+7–5=8.

4. Сначала Джек должен отмерить 300 граммов песка. Потом, положив на одну чашку весов 300 г песка и две гири, отмерить еще 600 г песка. И, наконец, положив на одну чашку весов 900 г песка и гирю в 200 г, отмерить еще 1100 г песка. Таким образом, всего он отмерит 2 кг песка.

5. Максимальное значение произведения – 9299, а минимальное значение второго множителя – 90. Таким образом, первый множитель не превосходит 9299:90. То есть возможные значения первого множителя – 100, 101, 102 и 103. Очевидно также, что второй множитель может принимать значения 90, 91 и 92. Перебирая различные варианты, получим следующие решения задачи: 100•92=9200, 101•92=9292, 102•91=9282, 103•90=9270.

 

6 класс

1. В магазине положили картофель в пакеты по 3 и 5 кг. Всего получили 24 пакета. Вес всех пакетов по 5 кг равен весу всех пакетов по 3 кг. Сколько было пакетов по 3 кг?

2. Найти восемь последовательных целых чисел так, чтобы сумма первых трех равнялась сумме пяти последних.

3. Можно ли покрыть равносторонний треугольник двумя другими равносторонними треугольниками меньшего размера?

4. Вовочка написал в вершинах пятиугольника числа, равные либо +1, либо –1. Петя перемножил числа, стоящие в соседних вершинах, и результаты записал на соответствующих сторонах пятиугольника. Как должен действовать Вова, чтобы среди получившихся 10 чисел было максимальное количество отрицательных?

5. Золотоискатель Джек добыл 9 кг песка. Сможет ли он за три взвешивания отмерить 2 кг песка с помощью чашечных весов с гирей 200 г?

Решения

1. Если взять 5 пакетов по 3 кг и 3 пакета по 5 кг, то в них будет поровну картошки, а всего таких пакетов будет 8. Но должно быть 24 пакета, поэтому надо взять в 3 раза больше 3-килограммовых и 5-килограммовых пакетов, то есть 15 и 9. Ответ: 15.

2. Пусть первое число x. Тогда x+(x+1)+(x+2)+(x+3)+(x+4) = (x+5)+(x+6)+(x+7) или 5x+10=3x+18, откуда x=4. Ответ: 4, 5, 6, 7, 8, 9, 10, 11.

3. Только одна вершина исходного треугольника может попасть в меньший по размерам равносторонний треугольник. Так как всего у треугольника три вершины. То для покрытия понадобится не менее трех треугольников.

4. Вова должен записать числа в таком порядке: 1, -1, 1, -1, -1. В этом случае на сторонах пятиугольника окажутся записанными 4 числа -1 и одна единица, то есть общее количество единиц будет равно 3. Меньшее число единиц получиться не может, так как если во всех вершинах пятиугольника поставить -1, то на его сторонах будет 5 единиц, если в 4 вершинах поставить -1, то на сторонах появится 3 единицы. Если же в вершинах две единицы расставить по-другому, то число единиц на сторонах может только возрасти.

5. Отвесим сначала 200 г песка. Затем положим на одну чашку весов гирю в 200 г и разложим оставшиеся 8 кг 800 г песка так, чтобы весы уравновесились. При этом на одной чашке окажется 4400 г песка, а на другой – 4600 г. При третьем взвешивании на одну чашку весов положим гирю в 200 г и 200 г песка, а затем разложим 4400 г песка так, чтобы весы уравновесились, при этом на одной чашке окажется 2400 г, а на другой 2 кг ровно.

 

7 класс

1. Федоту выставили годовые оценки по 12 предметам. Оказалось, что его средний балл равен 3,5. По скольким предметам в следующем году он должен улучшить свою оценку на один балл для того, чтобы средний балл стал равен 4?

2. Сколько найдется двузначных натуральных чисел, меньших 100, цифры которых идут в порядке возрастания?

3. Мне удалось, взяв по два раза цифры 1, 2, 3, 4, написать восьмизначное число, у которого между единицами стоит одна цифра, между двойками – две, между тройками – три, а между четверками – ровно четыре цифры. Что за число получилось?

4. В столовую привезли халву, но в дороге она раскрошилась на 2007 частей. Учитель математики сказал, что он сможет разрезать один кусок халвы на две части и после этого разложить халву на две кучки равной массы. Как он собирается это сделать?

5. Даны девять прямых, из которых никакие три не проходят через одну точку и любые две пересекаются. Какое наибольшее число прямых углов может образоваться в результате пересечения этих прямых?

6. Золотоискатель Джек добыл 9 кг песка. Сможет ли он за три взвешивания отмерить 2 кг песка с помощью чашечных весов с гирей 200 г?

Решения.

1. Сумма оценок равна 42. Если средний балл станет 4, то сумма станет 48, то есть возрастет на 6. То есть Федот должен улучшить на 1 балл оценку по 6 предметам.

2. Во втором десятке (от 10 до 19) таких чисел 8, в третьем десятке таких чисел 7, в четвертом – 6, в пятом – 5 и так далее. Всего таких чисел будет 8+7+6+5+4+3+2+1 = 36.

3. 41312432

4. Положим всю халву на одну чашку весов и начнем перекладывать по одному кусочку на другую. Когда при перекладывании очередного кусочка вторая чашка перевесит, надо взять этот кусочек и разрезать его на части. Замечание: в задаче не требуется выяснять, на какие именно части следует разрезать кусочек халвы, достаточно объяснить, почему можно обойтись одним кусочком.

5. Никакая из данных прямых не может быть перпендикулярна сразу двум из оставшихся, так как в этом случае эти прямые будут параллельны. Таким образом, максимальное количество прямых углов получится, если у нас из 7 прямых будут три пары перпендикулярных. Общее число прямых углов при этом будет равно 12.

6. Смотрите решение задачи 5 для 6 класса.

Олимпиада (2008 год)

 

 

5 класс

1. На сковороде могут одновременно жариться 2 котлеты. Каждую надо обжарить с обеих сторон, причём для обжаривания одной стороны требуются 2 минуты. Можно ли поджарить 3 котлеты за 6 минут?

2. Можно ли в таблицу 4 × 4 поставить числа – 1, 0 и 1 так, чтобы все 8 сумм чисел в строках и столбцах были различными?

3. Сумма вычитаемого, уменьшаемого и разности равна 26. Найти уменьшаемое.

4. Отлейте из цистерны 13 литров молока, пользуясь ведрами емкостью 17 литров и 5 литров.

5. В корзине лежат 30 грибов. Среди любых 12 из них имеется хотя бы один рыжик, среди любых 20 - хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине.

 

Решения.

1. Сначала надо обжарить первую сторону у первой и второй котлет, потом вторую сторону первой котлеты и первую сторону третьей котлеты, а затем вторую сторону второй и третьей котлет.

2. Да, можно.

1	1	1	1
1	1	1	0
-1	0	-1	-1
-1	-1	1	-1

 

3. Так как сумма вычитаемого и разности равна уменьшаемому, то из условия задачи следует, что удвоенное уменьшаемое равно 26, то есть уменьшаемое равно 13.

4. Три раза налить в 17-литровое ведро по 5 литров. На четвертый раз это ведро наполнится, а в пятилитровом ведре останется 3 литра. Тогда надо вылить из 17-литрового ведра молоко обратно в цистерну, а затем налить в него 3 литра и 2 раза по 5.

5. В корзине может быть только 11 не рыжиков, то есть рыжиков не менее 19. Точно так же в корзине может быть только 19 не груздей, значит груздей не менее 11. Так как всего грибов 30, то среди них должно быть ровно 19 рыжиков и 11 груздей.

6 класс

1. Сумма положительных чисел больше 10. Может ли сумма их квадратов быть меньше 1?

2. Существует ли натуральные a,b, такие, что ab(a + b) = 15015?

3. Винни Пух, Пятачок, Кролик и ослик Иа съели вместе 70 бананов, причем каждому что-то досталось, Винни Пух съел бананов больше всех, а Пятачок с Кроликом съели вместе 45 бананов. Сколько бананов съел Иа?

4. Один листок календаря закрывает частичку другого.

Какая частичка больше – закрытая или открытая?

 

5. Маляр может за один ход перейти на соседнюю по стороне клетку шахматной доски, после этого он должен перекрасить ее в противоположный цвет. Маляр ставится на угловую клетку доски, где все клетки белые. Докажите, что он может покрасить доску в шахматном порядке.

 

Решения.

6 класс.

1. Может. Возьмем 1001 число, равное 0,01. Сумма этих чисел равна 10,01, что больше 10. Квадрат каждого из этих чисел равен 0,0001, а сумма квадратов равна 0,1001, что меньше 1.

2. Нет, не существует. Число ab(a + b) обязательно будет четным.

3. Так как Пятачок с Кроликом съели 45 бананов, то кто-то из них съел не менее 23 штук. В то же время Винни Пух съел больше всех бананов, а, значит, не менее 24. Таким образом, Винни, Пятачок и Кролик съели вместе не менее 69 бананов. То есть Иа мог съесть только 1 банан.

4. Разделим закрытую часть календаря на 2

области (см. рисунок). Площадь верхней закрытой

области равна площади верхней незакрытой

 области, а площадь нижней закрытой области

больше, чем площадь нижней незакрытой. Поэтому

общая площадь закрытой части больше.

5. Наметим маршрут по шахматной доске, при котором мы каждый раз переходим на соседнюю клетку, причем становимся на каждую клетку по 1 разу (это сделать совсем легко). Занумеруем клетки этого маршрута цифрами от 1 до 64. Затем маляр проходит по этому маршруту до клетки с самым старшим номером среди тех, которые покрашены не так как нужно. Затем он возвращается по тому же маршруту до клетки с самым младшим номером среди тех, которые выкрашены неправильно. При этом каждый раз клетка, до которой доходит маляр, оказывается перекрашенной в правильный цвет, а, значит, что постепенно его маршрут становится все короче и короче, пока он не перекрасит все клетки правильно.

 

7 класс

1. У завхоза было трое одинаковых чашечных весов. В одних весах потерялась часть деталей, и теперь они могут показывать что угодно. Любые весы помещаются на чашку других весов. Как за два взвешивания определить неисправные весы?

2. Расставьте различные натуральные числа в таблицу 2 × 3 (2 строки, 3 столбца) так, чтобы произведения в столбцах были равны, и суммы в строках тоже были равны (но суммы могут отличаться от произведений).

3. Доказать, что сумма всех девяти двузначных чисел, составленных из трех данных цифр, делится на 11.

4. Из пункта А в пункт В выехала «Тойота». Одновременно навстречу ей из пункта В выехали «Жигули». Через 2 часа «Тойота» находилась на полпути между пунктом А и «Жигулями». Через какое время она окажется на полпути между «Жигулями и пунктом В?

5. Маляр может за один ход перейти на соседнюю по стороне клетку шахматной доски, после этого он должен перекрасить ее в противоположный цвет. Маляр ставится на угловую клетку доски, где все клетки белые. Докажите, что он может покрасить доску в шахматном порядке.

 

Решения

1. Взвесим двое весов с помощью третьих. Допустим, что одни весы при этом перевесили. Возможны два варианта. Если мы взвешивали на хороших весах, то более тяжелые весы исправны. Если мы взвешивали на неисправных весах, то весы, которые перевесили, тем более исправны. Таким образом после первого взвешивания мы точно будем знать одни исправные весы, после чего вторым взвешиванием на этих весах определим неисправные. Если же при первом взвешивании весы уравновесились, то мы, очевидно, взвешивали на неисправных весах (если на исправных весах взвешивать исправные и неисправные, то исправные перевесят). В этом случае неисправные весы определятся за одно взвешивание.

2. Расставим сначала числа так, чтобы произведения в столбцах были равны. Затем числа первой строки умножим на сумму чисел второй, а числа второй строки – на сумму чисел первой. Очевидно, что после этого будут выполнены оба условия задачи. Результат может быть, например, таким

17	102	68
132	22	33

3. Пусть a , b , c – эти цифры. Тогда из них можно составить числа 10 a + b , 10 b + a , 10 a + c , 10 c + a , 10 b + c , 10 c + b , 10 a + a , 10 b + b , 10 c + c . Складывая эти числа, получим 33 a +33 b +33 c . Очевидно, что это число делится на 11.

4. Пусть за два часа «Тойота» проехала х км, а «Жигули» y км. При этом расстояние между машинами в этот момент будет равно х км. За следующие два часа «Тойота» проедет еще х км, то есть окажется на расстоянии у км от пункта В, а «Жигули» проедут у км и окажутся на расстоянии 2у км от В. То есть еще через 2 часа «Тойота» окажется на полпути между пунктом В и «Жигулями».

5. Смотрите решение задачи 5 для 6 классов.

Олимпиада (2009 год)

 

 

5 класс

1. Пять учеников купили 100 тетрадей. Коля и Вася купили 52 тетради, Вася и Юра – 43 тетради, Юра и Саша -34 тетради, Саша и Сережа – 30 тетрадей. Сколько тетрадей купил каждый из них?

2. За круглым столом сидят 20 человек. Они хотят пересесть так, чтобы те, кто сидят рядом, сидели теперь через 2 человека. Возможно ли это?

3. Найти делимое и делитель в следующем примере: ***5:11 = **. Найти все решения и доказать, что других решений нет.

4. Из прямоугольника 3х9 вырезали две клетки (на рисунке они темные). Разрежьте оставшуюся фигуру на 3 части, из которых можно сложить квадрат 5 х 5.

5. На 22 карточках написаны натуральные числа 1, 2, …, 22. Из этих карточек составили 11 дробей. Какое наибольшее число этих дробей могут иметь целые значения?

 

Решения.

1. Коля, Вася, Юра и Саша купили вместе 52+34 = 86 тетрадей, поэтому Сережа купил 100 – 86 = 14 тетрадей. Саша купил 30 – 14 = 16 тетрадей, Юра купил 34 – 16 = 18 тетрадей, Вася купил 43 – 18 = 25 тетрадей, а Коля купил 52 – 25 = 27 тетрадей.

2. Возможно. Занумеруем все места за столом по часовой стрелке. Затем сидящего под номером 1 оставим на месте, сидящего под номером 2 пересадим на 4 место, сидящего под номером 3 – на 7 место, под номером 4 – на 10 место и так далее. Аккуратно проведя все эти пересадки, увидим, что условие, сформулированное в задаче, выполняется.

3. Так как 90∙11 = 990, а делимое является четырехзначным числом, то частное больше 90. В то же время, очевидно, что вторая цифра частного равна 5. Поэтому частное равно 95, то есть делимое равно 95∙11 = 1045.

4. Один из способов показан на рисунке.

5. Рассмотрим числа 13, 17, 19. Если какое-то из них будет стоять в знаменателе, то дробь будет несократима, а если в числителе, то дробь примет целое значение только тогда, когда в знаменателе стоит 1. То есть из 11 дробей всегда найдется одна несократимая. Десять дробей, принимающих целое значение, составить можно: 22/11, 21/7, 20/10, 19/1, 18/9, 16/8, 15/5, 14/2, 12/4, 6/3.

 

6 класс

1. Выписать в ряд числа 1, 2, 3, …, 10 так, чтобы сумма любого количества с начала стоящих чисел делилась на следующее за ними число.

2. Можно ли на доску 5 х 5 поставить 3 шахматных коня так, чтобы они били все незанятые ими клетки?

3. Передние покрышки автомобиля стираются через 25000 км пути, а задние – через 15000 км. Когда нужно поменять покрышки местами, чтобы они стерлись одновременно?

4. Класс, состоящий из 30 человек, во время дискотеки разбился на 5 групп по 6 человек, причем в любых двух группах оказалось разное количество девочек. Для медленного танца учитель захотел выбрать две группы A и Б, чтобы все ребята из группы A танцевали с ребятами из группы Б (девочки — с мальчиками, а мальчики — с девочками). Обязательно ли учитель найдет две такие группы?

5. К каждой грани кубика приклеили по такому же кубику. К каждой грани поверхности получившейся фигуры приклеили еще раз по такому же кубику (возможно, некоторые кубики закрыли две грани). Из какого количества квадратиков состоит поверхность полученного тела?

Решения

1. Например, возможна такая расстановка: 6, 1, 7, 2, 8, 3, 9, 4, 10, 5.

2. Если конь стоит в центральной клетке, то он бьет 8 клеток, если в любой другой — то не более 6. Тогда, три коня из 22 незанятых ими клеток могут бить не более 8 + 6 + 6 = 20. Значит, три коня расставить нельзя.

3. Чтобы покрышки стерлись одновременно, нужно, чтобы они одинаковое расстояние проехали на задних и передних колесах. Обозначим это расстояние через х. Тогда доля их изношенности на передних колесах равна , а на задних колесах . Поэтому . Решая это уравнение, получим x = 9375.

4. Всего в группе может быть 6 девочек, 5 девочек, …, 1 девочка или не быть девочек вообще. Предположим, что учителю не удастся найти такие группы. Тогда, группа, в которой 3 девочки, может быть только одна (1). Из вариантов, когда в группе 4 или 2 девочки возможен только один (иначе найдется искомая пара) (2); из вариантов, когда в группе 5 или 1 девочка также возможен один (3), как и для вариантов, когда в группе нет девочек и когда в группе нет мальчиков (4). Таким образом, возможны только 4 группы, а их всего 5. Противоречие. Значит, пара искомых групп всегда найдется.

5. Общий вид полученного тела можно увидеть на рисунке:

Если посмотреть на него сверху, то будет видно 13 квадратиков:

Также будет видно 13 квадратиков, если смотреть снизу, впереди, сзади, справа и слева. При этом каждый квадратик поверхности мы увидим, причем ровно 1 раз. Значит, поверхность состоит из 13 ∙ 6 = 78 квадратиков.

 

7 класс

1. Выписать в ряд числа 1, 2, 3, …, 16 так, чтобы сумма любого количества с начала стоящих чисел делилась на следующее за ними число.

2. На шахматной доске стоят 8 ладей так, что никакие две из них не бьют друг друга. Докажите, что на черных полях стоит четное число ладей.

3. Из трех квадратов, длины сторон которых составляют целое число сантиметров, сложили прямоугольник. Найти его периметр, если площадь равна 96см²?

4. Сколько килограммов воды нужно выпарить из 0,5 тонн целлюлозной массы, содержащей 85% воды, чтобы получить массу, содержащую 70% воды?

5. На планете Куб (имеющей форму куба) каждой гранью владеет рыцарь (который всегда говорит правду) или лжец (который всегда врет). Каждый из них утверждает, что большая часть его соседей — лжецы. Сколько рыцарей и сколько лжецов владеет гранями планеты?

 

Решения.

1. Например, возможна такая расстановка: 9, 1, 10, 2, 11, 3, 12, 4, 13, 5, 14, 6, 15, 7, 16, 8.

2. Занумеруем столбцы и строки шахматной доски числами от 1 до 8. Тогда сумма координат черной клетки – четное число, а сумма координат белой клетки – число нечетное. Чтобы 8 ладей не били друг друга, все они должны стоять в разных строках и разных столбцах, поэтому сумма координат всех клеток, на которых стоят ладьи, равна 2∙(1+2+…+8), то есть является четным числом. Но это означает, что на белых клетках не может стоять нечетное число ладей. А значит и на черных клетках число ладей тоже будет четным.

3. Из трех квадратов составить прямоугольник можно только двумя способами.

Первый способ:

Второй способ:

В первом случае площадь каждого квадрата — треть площади прямоугольника, но тогда площадь каждого квадрата — 32см². Это невозможно, так как сторона каждого квадрата должна быть целым числом.

Значит, квадраты расположены вторым способом. При этом суммарная площадь маленьких квадратов — половина площади большого, поэтому составляет 96:3 = 32см², то есть площадь маленького квадрата — 16см², а сторона — 4см. Нетрудно подсчитать, что тогда периметр прямоугольника равен 40см.

4. 500 кг целлюлозной массы содержат 425 кг воды и 75 кг сухого вещества. После того, как часть воды испарится, эти 75 кг будут составлять 30% новой целлюлозной массы. То есть новая целлюлозная масса будет весить 250 кг. Значит, испарится 250 кг воды.

5. Если бы на планете жили три рыцаря, то один из них был соседом двух других, значит, у него соседи-лжецы составляли не более половины всех соседей. Если бы на планете не было рыцарей или жил только один рыцарь, то нашелся бы лжец, все соседи которого — лжецы. Он не может заявить, что большая часть его соседей — лжецы, так как он должен соврать. Значит, на планете ровно два рыцаря (условие задачи выполняется, если они владеют противоположными гранями планеты).

Приложение

Избранные задачи школьных олимпиад.

 

8 класс

 

1. Известно, что x+y+z+t=0. Доказать, что x³+y³+z³+t³ = 3×(xy–zt)×(z+t).

2. По кругу расставлены восемь точек. Двое по очереди соединяют их отрезками. Первый отрезок проводится произвольно, а каждый следующий отрезок начинается из конца предыдущего. Проигрывает тот, кто не может провести новый отрезок (дважды проводить отрезок нельзя). Предположим, что игроки не делают ошибок. Кто из них победит: первый или второй?

3. Обозначим s(x) сумму цифр числа х. Пусть а=99⁹⁹, b=s(a), c=s(b), d=s(c). Чему равно d?

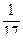
4. Верно ли неравенство:   +  +...+ < 2

 

Решения.

1. Из условия задачи следует, что x+y=–(z+t), а потому (x+y)³=–(z+t)³;

x³+y³+3xy(x+y)=–z³–t³–3zt(z+t);

x³+y³–3xy(z+t)=–z³–t³–3zt(z+t);

x³+y³+z³+t³=3xy(z+t)– 3zt(z+t)=3(z+t)(xy–zt), что и требовалось доказать.

2. При правильной игре первый игрок выиграет. Докажем это. Занумеруем точки по часовой стрелке числами от 1 до 8. Первый ход можно сделать произвольно, например, соединить точку 1 с точкой 2. В какую бы точку ни провел отрезок второй игрок, первый игрок должен вернуться в точку 1. После следующего хода он должен вернуться в точку 2, затем снова в точку 1 и т.д., пока у второго игрока не кончатся ходы. Например, игра может развиваться так: 1 – 2 – 3 – 1 – 4 – 2 – 5 – 1 – 6 – 2 – 7 – 1 и у второго игрока больше нет ходов.

3. В числе a не больше 9900 знаков. Поэтому b = s(a)<99000, c = s(b)<50, d = s(c)<18. Так как число a делится на 9, то таким же свойством обладают и остальные числа (это следует из признака делимости на 9). Так как, очевидно, d>0, то  d = 9.

4. Каждое из 5 первых слагаемых не больше 0,2, а каждое из 8 остальных слагаемых меньше 0,125, поэтому сумма всех слагаемых меньше 2.

 

9 класс

 

1. Существует ли 100-значное число, которое при изменении любой цифры остается составным?

2. Через вершины А и В треугольника АВС проведены две прямые, которые разбивают треугольник на четыре фигуры (три треугольника и один четырехугольник). Известно, что три из этих фигур имеют одинаковые площади. Доказать, что четырехугольник среди них.

3. Какое наименьшее число коней может побить все поля шахматной доски? (Поле, на котором стоит конь, считается побитым).

4. На двух сторонах треугольника как на диаметрах построены окружности. Доказать, что круги покрывают весь треугольник.

 

Решения.

1. Существует, например 4618900...010 (между 9 и 1 - 93 нуля). При замене последней цифры на 1, 3, 7 или 9 это число будет делиться соответственно на 11, 13, 17 или 19 - поскольку 46189 делится на них. При замене последней цифры на четную или замене другой цифры число будет четным, а при замене последней цифры на 5 - кратным 5.

2. Пусть данные прямые пересекают стороны ВС и АС в точках К и Р соответственно. Если все треугольники имеют равные площади, тогда отрезки АК и ВР делятся точкой пересечения пополам, а это значит, что АРКВ – параллелограмм, чего быть не может.

3. 12 коней. Пример: кони на b3,c3,c4,c6,c7,d6,f5,f6,g6, e3,f3,f2. (Позиция переходит в себя при повороте на 90 градусов) Покажем, что 12 коней необходимы. Разобьем доску на 4 квадрата 4х4. Рассмотрим, например нижний левый квадрат. В нем есть поля a1,a2 и b2, которые не могут побить кони из других квадратов. Никакой конь не может побить одновременно два из этих полей, поэтому в этом квадрате должно быть не меньше трех коней. То же верно для остальных квадратов, поэтому всего коней не менее 12.

4. Пусть АС и АВ – диаметры кругов, АН – высота треугольника. Тогда круг с диаметром АС покрывает треугольник АНС, а круг с диаметром АВ – треугольник АНВ. Отсюда следует, что два круга вместе покрывают исходный треугольник.

 

10 класс

 

1. Имеют ли общие действительные корни многочлены x⁴+x³+x²+1 и –x⁴+x²+2x+1?

2. На сторонах AB, BC, CD и AD прямоугольника ABCD взяты точки K, L, M, N соответственно. Докажите, что периметр четырехугольника KLMN не превосходит 2АС.

3. Докажите, что сумма попарных произведений трех последовательных натуральных чисел не может равняться числу, десятичная запись которого состоит из одних шестерок.

4. Решить в целых числах уравнение x ² + y ² + z ² =2 xyz.

5. Решить неравенство

 

 

Решения

1. Рассмотрим систему   Второе уравнение системы преобразуем к виду (x+1)²–x⁴ = 0 или (x+1–x²)(x+1+x²) = 0. Второй сомножитель положителен при всех действительных x, значит x+1–x² = 0. Умножим это уравнение на x² и вычтем из (1); получим уравнение 2x⁴+1=0, которое не имеет решения. Отсюда следует, что общих корней исходные уравнения не имеют.

2. Пусть точка К₁ симметрична точке К относительно прямой ВС, точки N₁ и К₂ симметричны точкам N и К относительно прямой CD, а точка К₃ симметрична точке К₂ относительно прямой AD. Тогда длина ломаной K₁LMN₁K₃ равна периметру четырехугольника KLMN, а с другой стороны К₁К₃ = 2АС, откуда следует утверждение задачи.

3. Пусть n, n–1, n+1 – эти числа. Сумма их попарных произведений равна 3n²–1, т.е. не делится на 3, в то время как число, записанное с помощью шестерок, на 3 делится.

4. Докажем, что x, y, z – четные числа. Пусть это не так. Тогда два из них нечетные. Пусть, например, x=2a+1, y=2b+1, z=2c. Тогда, как нетрудно видеть, правая часть уравнения делится на 4, а левая не делится. Значит, x, y, z – четные числа. Обозначим x=2a, y=2b, z=2c и подставим в исходное уравнение. Получим уравнение a ² + b ² + c ² =4 abc , из которого следует, что a, b, c – четные, т.е. x, y, z делятся на 4. Аналогично доказывается, что x, y, z делятся на 8, 16 и т.д. Отсюда следует, что x=y=z=0.

5. Положим a=x⁴+x²+1, b=x⁴–x²+3. Заметим, что при любых значениях x a и b – положительные числа. Используя введенные обозначения, перепишем исходное неравенство в виде , что равносильно неравенству , которое справедливо лишь при a=b. Приравнивая а и b, получим 2x²=2, т.е. x=±1.

 

11 класс

 

1. Доказать ,что если a­­­²+b²+ab+bc+ca<0, то a²+b² < c².

2. В ряд выложено 30 шаров, 15 красных и 15 синих. Доказать, что найдется 10 лежащих подряд шаров, среди которых поровну красных и синих.

3. Функция f(x) определена на множестве действительных чисел и при всех x удовлетворяет условию 2f(x)+f(1–x)=x². Найти f(x).

4. Первоначально на доске написано натуральное число А. Разрешается прибавить к нему один из его делителей, отличных от него самого и единицы. С полученным числом разрешается проделать аналогичную операцию, и т.д. Докажите, что из числа А=4 можно с помощью таких операций прийти к любому наперед заданному составному числу.

 

Решения

1.

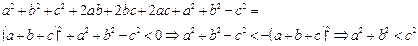
2. Обозначим через а_к число красных шаров среди тех десяти шаров, которые начинаются с к-го. Рассмотрим а₁, а₁₁ и а₂₁. Сумма этих чисел равна 15. Если одно из них равно 5, то задача решена. В противном случае по крайней мере одно из этих чисел больше 5, а одно – меньше. Пусть, например, а₁>5, a₁₁<5. Будем менять к от 1 до 11. При этом за один раз а_к может измениться только на единицу, поэтому на каком-то шаге получим а_к=5.

3. Подставим в исходное уравнение 1– x вместо x и получим 2f(1–x)+f(x)=x². Умножив это равенство на –2 и сложив с исходным, найдем .

4. Заметим, что если к A прибавить его делитель d, то A+d снова будет делиться на d, поэтому делитель можно прибавлять любое число раз подряд. Если число В четно, то решение очевидно. Всякое нечетное составное число B можно представить в виде B=cd, где 3≤c≤d. Прибавим к A=4 (c-2) раза делитель 2, получим число 2c; теперь (d-2) раза прибавим делитель c, получим число В=cd.

 

 

---

Дата добавления: 2019-01-14; просмотров: 540; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!