Городская математическая олимпиада (2006 год)

Условия задач

8 класс

1. Какое наименьшее значение может принимать выражение a² – 6a + b² + 4b?

2. Во дворе живут 4 песика: Бобик, Робик, Тобик и Толстолобик. Каждому из них случалось драться с кем-нибудь из остальных, причем у Бобика, Робика и Тобика число тех, с кем они дрались - разное. Со сколькими собаками двора дрался Толстолобик?

3. По кругу выписаны 12 чисел. Сумма любых трех соседних чисел равна 7. Чему равна сумма всех чисел?

4. 4 белых кирпича и 3 красных вместе весят меньше 21 фунта, а 7 белых и 4 красных - больше 33 фунтов. Какой кирпич увесистей - белый или красный?

5. На гипотенузе АВ прямоугольного треугольника АВС взяты точки М и К такие, что ВС = ВМ и АС = АК. Докажите, что ÐМСК = 45°.

9 класс

1. По кругу выписаны 12 чисел. Сумма любых трех соседних чисел равна 7. Чему равна сумма всех чисел?

2. 4 белых кирпича и 3 красных вместе весят меньше 21 фунта, а 7 белых и 4 красных - больше 33 фунтов. Какой кирпич увесистей - белый или красный?

3. Какие коэффициенты должны быть у многочлена x⁶+px⁴+qx²+r, чтобы он являлся полным квадратом?

4. Докажите, что прямая, которая касается описанной вокруг треугольника АВС окружности в точке А, параллельна прямой, проходящей через основания высот ВВ₁и СС₁ этого треугольника.

5. Найти два действительных корня уравнения х⁴+41х+а=0, если известно, что это различные целые числа.

10 класс

1. Какое из чисел больше: a = 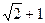или b = ?

2. На какое наименьшее число кусков следует разрезать кусок проволоки длиной 12 метров, чтобы их них можно было спаять каркас куба с ребром 1 метр (проволоку разрешается сгибать)?

3. Найти два действительных корня уравнения х⁴+41х+а=0, если известно, что это различные целые числа.

4. При каких значениях а уравнение имеет решение?

5. На основаниях трапеции вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей.

11 класс

1. Решить уравнение sinx= [x], где [x] – целая часть х, то есть наименьшее целое число, не превосходящее х.

2. Найдите наименьшее значение выражения (x+y)(x+z), если x, y и z – положительные числа и xyz(x+y+z) = 1.

3. При каких значениях а уравнение 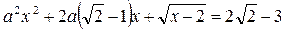имеет решение?

4. В выпуклом четырехугольнике ABCD биссектрисы углов А и В пересекаются в точке М, а биссектрисы углов С и D пересекаются в точке N. Известно, что точки М и N различны и MN^AB. Докажите, что ÐА = ÐВ.

5. Существует ли треугольная пирамида, площади боковых граней которой равны 5, 6 и 7, а радиус вписанной сферы равен 1?

Решения

8 класс

1. a² – 6a + b² + 4b = a² – 6a + 9 + b² + 4b + 4 – 13 = (а–3)²+(b+2)²–13. Так как (а–3)²≥0 и (b+2)²≥ 0, то –13 будет минимальным значением, которое принимает данное выражение.

2. Число соперников каждого из песиков может принимать значения 1, 2 и 3. Так как Бобик, Робик и Тобик имеют разное число соперников, то кто-то из них дрался с тремя, кто-то – с двумя, а кто-то – с одним. Пусть Бобик дрался с тремя, в том числе и с Толстолобиком, а Тобик – с одним. Но тогда Тобик дрался только с Бобиком, а потому Робик, который имеет двух соперников, должен был драться с Толстолобиком. Таким образом, Толстолобик дрался с двумя собаками.

3. Обозначим числа а₁, а₂,…, а₁₂. Тогда а₁+ а₂+а₃=7, а₂+а₃+а₄ =7, … , а₁₂+ а₁+а₂ =7. Сложив эти равенства будем иметь 3(а₁+ а₂+а₃+…+ а₁₂)=7×12=84. Поэтому сумма всех чисел равна 28.

4. Пусть х – вес белого кирпича, а у – красного. Тогда 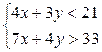. Умножим первое неравенство на -33, а второе – на 21 и сложим полученные неравенства. В результате будем иметь, что 15х – 15у > 0, то есть x>y. Таким образом, белый кирпич тяжелее красного.

5. 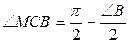; 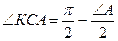. 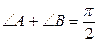, отсюда . Сумма углов МСВ и КСА равна , т.е. она больше прямого угла на угол 45°. Отсюда видно, что эти углы имеют общую часть. Она и есть искомый угол МСК, равный 45°.

9 класс

1. Смотрите решение задачи 3 для 8 классов.

2. Смотрите решение задачи 4 для 8 класса.

3. Допустим, что данный многочлен получается при возведении в квадрат многочлена Р(х). Очевидно, что Р(х) – приведенный многочлен третьей степени, у которого отсутствует слагаемое второй степени (иначе при возведении в квадрат получится слагаемое пятой степени). Так как в многочлене 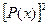нет слагаемого первой степени, то у Р(х) отсутствует либо слагаемое первой степени, либо свободный член. Таким образом, возможны два случая: Р(х) = х³+ах или Р(х) = х³+b. В первом случае имеем r=0, р=2а и q=a², откуда p²=4q. Во втором случае в многочлене 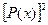появляется слагаемое третьей степени, что противоречит условию.

Ответ: r=0, p²=4q.

4. Если построить на стороне ВС как на диаметре окружность, то она пройдет через точки С₁ и В₁. Но тогда углы ВВ₁С₁ и ВСС₁ равны, а, значит, равны и углы АВС и АВ₁С₁. Но прямая, которая касается описанной вокруг треугольника АВС окружности в точке А, составляет со стороной АС угол, равный углу АВС, откуда следует, что эта прямая параллельна В₁С₁.

5. Пусть n и m – корни данного уравнения. Тогда n⁴+41n+a = 0, m⁴+41m+a = 0. Вычтем из первого уравнения второе и получим n⁴–m⁴+41(n–m) = 0 или (n–m)(n+m)(т²+m²)+41(n–m) = 0. Так как n–m ¹ 0, то (n+m)(т²+m²)= –41. Возможны два случая: или . В первом случае получаем числа 4 и – 5, вторая система не имеет решения.

10 класс

1. 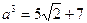; b³=14, откуда имеем, что 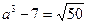, а это больше, чем b³–7= . Получили, что a>b.

2. Поскольку в каждой вершине сходятся три ребра, то при изготовлении каркаса в каждой вершине должен находиться конец какого-то куска проволоки. Следовательно, общее число кусков не меньше четырех. С другой стороны, нетрудно придумать пример каркаса, сделанного из четырех кусков проволоки.

3. Смотрите решение задачи 5 для 9 классов.

4. Уравнение легко приводится к виду 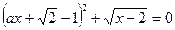, откуда следует, что оба слагаемых в этой сумме равны 0. Это означает, что х=2, .

5. Рассмотрим гомотетию относительно точки О пересечения диагоналей трапеции с коэффициентом , где а и b – длины оснований трапеции. Эта гомотетия переводит основание длины а в основание длины b. Следовательно, и квадрат со стороной а переходит в квадрат со стороной b, а потому центры этих квадратов лежат на одной прямой.

11 класс

1. Возможны три случая: 1) sinx= 1, 1≤х<2; 2) sinx= 0, 0≤х<1; 3) sinx= –1, –1≤х<0. В первом случае решением уравнения будет 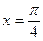, во втором случае х=0, в третьем случае решения нет.

2. (x+y)(x+z) = x(x+y+z) + yz ≥ 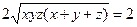(было использовано неравенство между средним арифметическим и средним геометрическим). С другой стороны, если y=z=1, а 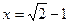, то (x+y)(x+z) = 2. Таким образом, 2 – минимальное значение этого выражения.

3. Смотрите решение задачи 4 для 10 класса.

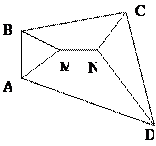Точка М равноудалена от прямых АВ и ВС, а также от прямых АВ и АD, поэтому она равноудалена от прямых ВС и АD. Аналогично, т. N равноудалена от ВС и АD. Если прямые ВС и АD пересекаются, то MN – биссектриса угла, ими образованного, и, следовательно, прямые ВС и АD симметричны относительно прямой MN. Если ВС и АD параллельны, то все равно они симметричны относительно MN. При указанной симметрии прямая АВ переходит в себя, т.к. она перпендикулярна MN. Таким образом, угол АВС перейдет в угол BAD. Значит, эти углы равны.

5. Нет. Предположим противное и проведем через центр вписанной сферы плоскость, параллельную той боковой грани, которая имеет площадь 5. В сечении получится треугольник, площадь которого будет меньше, чем площадь этой грани, причем внутри этого треугольника будет содержаться круг радиуса 1. Однако известно, что среди всех треугольников, описанных вокруг данной окружности, наименьшую площадь имеет равносторонний, площадь которого в данном случае равна , что больше 5.

Дата добавления: 2019-01-14; просмотров: 399; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 Следующая ⇒

Мы поможем в написании ваших работ!