Городская математическая олимпиада (2007 год)

Условия задач

8 класс

1. Можно ли между числами 1, 2, 3, …49, 50 расставить знаки сложения, вычитания и скобки так, чтобы после выполнения указанных действий результат оказался равным 0?

2. На занятии Вася, Леня и Стас решили все задачи. Может ли оказаться, что Стас большинство задач решил раньше Лени, Леня – большинство раньше Васи, а Вася – большинство раньше Стаса?

3. На гипотенузе АВ прямоугольного треугольника АВС взяты точки М и К такие, что ВС = ВМ и АС = АК. Докажите, что ÐМСК = 45°.

4. Имеются 300 яблок, любые два из которых различаются по весу не более чем в два раза. Докажите, что их можно разложить в пакеты по два яблока так, чтобы любые два пакета различались по весу не более, чем в полтора раза.

5. Петя отправился пешком из лагеря в поселок. В 12:00, когда Петя был в а км от лагеря, его нагнал велосипедист и подвез на некоторое расстояние, высадив в а км от поселка. После этого Петя пришел в поселок в 14:00. Сколько времени потребуется Пете на обратный путь пешком, если на велосипеде он ехал в два раза быстрее, чем шел пешком.

9 класс

1. Можно ли увезти на 7 трехтонных грузовиках 50 камней весом 370 кг, 372 кг, 374 кг, … , 468 кг?

2. Дан набор, состоящий из 2007 чисел таких, что если каждое число в наборе заменить на сумму остальных, то получится тот же набор. Докажите, что хотя бы одно из чисел в наборе равно 0.

3. Петя отправился пешком из лагеря в поселок. В 12:00, когда Петя был в а км от лагеря, его нагнал велосипедист и подвез на некоторое расстояние, высадив в а км от поселка. После этого Петя пришел в поселок в 14:00. Сколько времени потребуется Пете на обратный путь пешком, если на велосипеде он ехал в два раза быстрее, чем шел пешком.

4. В лес пошло 11 девочек и n мальчиков. Вместе они собрали n²+9n–2 гриба, причем все дети собрали поровну грибов. Кого было больше: мальчиков или девочек?

5. Биссектриса угла A треугольника ABC пересекает серединный перпендикуляр стороны AB в точке X, серединный перпендикуляр стороны AC – в точке Y, а описанную окружность треугольника – в точке Z. Точки A, X, Y, Z лежат на биссектрисе в порядке перечисления. Докажите, что AX = YZ.

10 класс

1. Дана функция 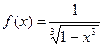.Найдите .

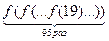2. Двое по очереди закрашивают клетки квадрата 2007х2007, причем им запрещается раскрашивать клетки, имеющие общую сторону с ранее закрашенной клеткой. Проигравшим считается тот, кто не сможет закрасить очередную клетку. Кто выиграет при правильной игре: первый игрок или второй?

3. Существуют ли такие целые числа x₁, x₂, …, x₁₀₀₀₀, что ?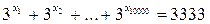

4. Найти наименьшее значение выражения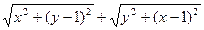

5. Пусть две окружности разных радиусов касаются друг друга внутренним образом в точке А. Через точку меньшей окружности В (В не равна А), проведена касательная к меньшей окружности, которая пересекает большую окружность в точках К и М. Доказать, что прямая АВ является биссектрисой угла КАМ.

11 класс

1. Решить уравнение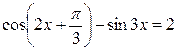

2. Первоначально на доске написано натуральное число А. Разрешается прибавить к нему один из его делителей, отличных от него самого и единицы. С полученным числом разрешается проделать аналогичную операцию, и т.д. Докажите, что из числа А = 4 можно с помощью таких операций прийти к любому наперед заданному составному числу.

3. Все стороны и диагонали правильного 12-угольника раскрашены в 12 цветов (каждый отрезок – одним цветом). Существует ли такая раскраска, что для любых трех цветов найдутся три вершины, попарно соединенные между собой отрезками этих цветов.

4. Докажите тождество

5. В тетраэдре ABCD ребро АВ перпендикулярно ребру CD, а ребро ВС – ребру AD. Найти длину отрезка АВ, если AD=a, BC=b, CD=c.

Решения

8 класс

1. Среди данных чисел 25 нечетных, поэтому их сумма (какие бы знаки в ней ни стояли) будет нечетным числом. То сделать ее равной 0 невозможно.

2. Такое возможно. Например, если общее число задач равнялось трем, причем первую задачу мальчики решили в следующем порядке: Стас, Леня, Вася; вторую задачу – Вася, Стас, Леня; третью – Леня, Вася, Стас.

3. ; . , отсюда . Сумма углов МСВ и КСА равна , т.е. она больше прямого угла на угол 45°. Отсюда видно, что эти углы имеют общую часть. Она и есть искомый угол МСК, равный 45°.

4. Занумеруем яблоки в порядке неубывания весов и положим в k-й пакет яблоки с номерами k и 301–k. Рассмотрим два произвольных пакета. Пусть в одном из них яблоки с весами а £ d, а в другом – с весами b £ с. Тогда а £ b £ c £ d. Имеем: а+d £ c+2b £ 1.5c+1.5b и b+c £ 2а+d £ 1.5a+1.5d, что и требовалось.

5. Пусть v – скорость Пети, S – расстояние от лагеря до поселка. Тогда 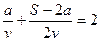, откуда следует, что , то есть 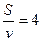. С другой стороны, время, которое Петя затратит на обратный путь, как раз и равно .

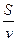9 класс

1. Нет, поскольку в одном из грузовиков должно оказаться не менее 8 камней, а вес 8, даже самых легких, камней превышает 3 тонны.

2. Пусть сумма чисел в наборе равна М, тогда число а из набора заменяется на число b=М–а. Просуммируем эти равенства для всех а: b₁+…+b₂₀₀₇=2007M–(a₁+…+a₂₀₀₇), откуда М=0, т.к. b₁+…+b₂₀₀₇=а₁+…+а₂₀₀₇=М. Значит для любого а число b=–а также входит в набор и все числа разбиваются на пары а, –а. Из нечетности их количества следует, что в набор входит число а=–а, т.е. а=0.

3. Смотрите решение задачи 5 (8 класс).

4. Общее количество детей обозначим через х. Тогда n=х–11. Заметим, что х>11. Выразим общее число грибов через х: n²+9n–2=(х–11)²+9(х–11)–2=х²–13х+20. Это число равно х × k, где k – число грибов собранных одним человеком. Отсюда следует, что 20 делится на х. Есть единственный вариант, при котором х>11: х=20. Значит, мальчиков было 9.

5. Пусть O – центр описанной окружности треугольника ABC, а M и N –середины сторон AC и AB соответственно. Ясно, что оба серединных перпендикуляра проходят через точку O. Заметим, что OA = OZ как радиусы, кроме того, треугольники AXN и AYM подобны по двум углам. Значит, углы AXN и AYM равны. Тогда равны и углы OXY и OYX, а значит, OX = OY. Но тогда отрезки AX и ZY будут симметричны относительно серединного перпендикуляра к AZ, следовательно, они будут равны.

10 класс

1. Функция f ( x ) определена при всех x ¹1. Так как f ( x ) ¹0 при всех x, а f ( x ) = 1 лишь при x = 0, то выражение f ( f (… f ( x )…)) имеет смысл при всех x¹1. Нетрудно убедиться, что , а f ( f ( f ( x ))) = x. Т.к. 95 дает при делении на 3 остаток 2, то .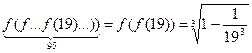

2. Первый игрок одержит победу. Для этого он должен первым ходом закрасить центральную клетку и в дальнейшем закрашивать клетки, симметричные тем, которые закрашивает его противник.

3. Нет. Допустим, что такие числа нашлись. Умножим равенство на достаточно большую степень тройки так, чтобы все слагаемые слева стали целыми. Тогда слева окажется сумма 10000 нечетных чисел – четное число, а справа – произведение нечетных чисел, т.е. нечетное число. Противоречие.

4. Рассмотрим на координатной плоскости точки А(0;1), В(1;0) и M(x;y). Тогда данное выражение равно сумме длин отрезком АМ и ВМ. Очевидно, что оно принимает минимальное значение, если точка М лежит на отрезке АВ, и значение это равно длине отрезка АВ, то есть .

5. Пусть О₁ – центр меньшей окружности, О₂ – центр большей окружности, L – точка пересечения прямой АВ и большей окружности. Треугольники LО₂А и ВО₁А подобны по трём углам поэтому LО₂ ВО₁, ВО₁ 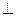КМ LО₂ КМ . Поэтому касательная к большей окружности проведённая через точку L будет параллельна КМ дуги LМ и КL равны прямая АВ является биссектрисой угла КАМ.

11 класс

1. Левая часть уравнения достигает своего максимального значения, равного 2, в том и только в том случае, когда выполнены условия: . Решая эту систему, получим . Изображая найденные значения на тригонометрической окружности, получим, что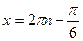

2. К числу 4 можно много раз прибавить число 2, при этом каждый раз получаются четные числа, у которых опять есть делитель 2, так что его снова можно прибавить. Таким образом можно получить все четные числа. Допустим теперь, что нужно получить нечетное составное число mn, m>2, n>2. Сначала получим четное число 2m, которое имеет делитель m; будем прибавлять его до тех пор, пока не получим число mn.

3. Допустим, что такая раскраска возможна. Рассмотрим отрезки какого-то одного цвета, например, красного. Общее число треугольников, одна из сторон которых красная, не меньше, чем число пар из остальных 11 цветов, т.е. 55. Так как каждый отрезок служит стороной для 10 треугольников, то число красных отрезков не меньше 6, а общее число отрезков должно быть не меньше 72. Однако число всех сторон и диагоналей в12-угольнике равно 66. Полученное противоречие показывает, что требуемая раскраска невозможна.

4. Сгруппируем слагаемые в левой сумме следующим образом: 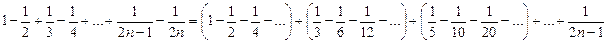(некоторые группы при этом будут состоять из одного слагаемого). Нетрудно видеть, что сумма слагаемых в каждой группе равна одному из слагаемых в правой части доказываемого равенства, при этом у разных групп получаются разные суммы. Так как число слагаемых в правой части и число групп в левой части совпадают, то должны совпадать и значения левой и правой сумм.

5. Пусть АВ = x. Достроим треугольник АВС до параллелограмма АВСЕ. Тогда АВ = СЕ = х, BC = AE = b. Так как AD перпендикулярно ВС, а ВС параллельно АЕ, то угол DAE прямой. Аналогично угол DCE прямой. Применяя теорему Пифагора к треугольникам ADE и DCE, получим, что х²+с² = a²+b², откуда найдем х.

Дата добавления: 2019-01-14; просмотров: 228; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒

Мы поможем в написании ваших работ!