Городская математическая олимпиада (2005 год).

Условия задач

8 класс

1. Каждым ударом силач Шварценеггер может разбить один кусок бетона на три части. За сколько ударов он расколет бетонную плиту на 27 кусков?

2. Может ли разность между трехзначным числом и числом, записанным теми же цифрами, но в обратном порядке, быть квадратом натурального числа?

3. Каждую грань кубика разбили на 4 равных квадрата и раскрасили эти квадраты в три цвета так, чтобы квадраты, имеющие общую сторону, были покрашены в разные цвета. Докажите, что в каждый цвет покрашено по 8 квадратов.

4. В треугольнике две высоты не меньше сторон, на которые они опущены. Найти углы треугольника.

5. Вода из родника течет двумя струями – одна сильнее, другая слабее. Человек подошел к роднику с кувшинами в 5 литров и 4 литра. Он поставил одновременно один кувшин под одну струю, а другой под вторую. Когда меньший кувшин наполнился на половину, человек поменял кувшины местами. Кувшины наполнились одновременно. Во сколько раз больше воды дает одна струя, чем другая?

6. Пятеро друзей скинулись на покупку. Могло ли при этом оказаться, что любые два друга в сумме внесли менее одной трети общей стоимости?

7. Докажите, что медиана АМ в треугольнике АВС по длине больше чем .

9 класс

1. В ящике лежат 70 шаров: 20 белых, 20 черных, 20 красных, остальные – синие и зеленые. Шары отличаются только цветом. Какое наименьшее число шаров надо взять, чтобы среди них оказалось не менее 10 шаров одного цвета.

2. Каждую грань кубика разбили на 4 равных квадрата и раскрасили эти квадраты в три цвета так, чтобы квадраты, имеющие общую сторону, были покрашены в разные цвета. Докажите, что в каждый цвет покрашено по 8 квадратов.

3. Пятеро друзей скинулись на покупку. Могло ли при этом оказаться, что любые два друга в сумме внесли менее одной трети общей стоимости?

4. Вычислить .

5. Медиана прямоугольного треугольника, проведенная к гипотенузе, делит его на два треугольника, имеющих периметры 8 и 9 см. Найти стороны треугольника.

6. Доказать, что при всех значениях а и b справедливо неравенство: .

7. Точки A, B, C, D расположены на плоскости так, что AC ^ BD и AB ^ CD. Докажите, что AD ^ BC.

10 класс

1. В каждой из двух урн находится произвольное не равное нулю число шаров. Разрешается одновременно удалять из урн одинаковое число шаров и удваивать число шаров в одной из урн. Доказать, что с помощью этих операций можно удалить из урн все шары.

2. Найти наименьшее число, при делении которого на 2 получается точный квадрат, а при делении на 3 –точный куб.

3. Существует ли многогранник, имеющий ровно 7 ребер?

4. Пять отрезков таковы, что из любых трех можно составить треугольник. Доказать, что хотя бы один из этих треугольников остроугольный.

5. Доказать, что при всех значениях а и b справедливо неравенство: .

6. В турнире по футболу участвовало n команд. Известно, что ни один из матчей не закончился вничью. Доказать, что сумма квадратов чисел, задающих количество побед каждой команды равна сумме квадратов чисел, задающих количество их поражений.

7. Дан прямоугольный треугольник АВС с катетами АВ =8 и ВС = 6. Проведена медиана ВМ. Прямая l параллельна АВ и пересекает отрезки АМ, ВМ и ВС соответственно в точках P, Q, R. Найти наименьшее значение S_PMQ+S_BQR.

11 класс

1. Вычислить .

2. В турнире по футболу участвовало n команд. Известно, что ни один из матчей не закончился вничью. Доказать, что сумма квадратов чисел, задающих количество побед каждой команды равна сумме квадратов чисел, задающих количество их поражений.

3. В каждой клетке доски размером NxM стоит шашка. Играют двое. За один ход игрок может взять любое количество подряд стоящих шашек в любом горизонтальном или вертикальном ряду. Ходят по очереди. Выигрывает тот, кто возьмет последнюю шашку. Считаем, что игроки играют наилучшим образом. Какой игрок победит. Укажите, как он должен играть.

4. Две окружности касаются друг друга внешним образом в точке D. Прямая касается одной из них в точке А и пересекает другую в точках В и С. Докажите, что точка А равноудалена от прямых BD и CD.

5. Решите уравнение х³–у³ = ху+61, где х и у – натуральные числа.

6. Сравнить числа 99! И 50⁹⁹.

7. Длины двух скрещивающихся ребер тетраэдра равны а, двух других – b, еще двух – с. Найти объем тетраэдра.

Решения.

8 класс

1. Сначала был один кусок. С каждым ударом число кусков увеличивается на 2. Таким образом, чтобы кусков стало 27, надо произвести 13 ударов.

2. (100a+10b+c) – (100c+10b+a) = 9·11(a–c) = 3·3·11(a–c). Так как a–c<11, то не может.

3. Разобьем квадраты на 8 групп так, чтобы квадраты из одной группы имели своей общей вершиной вершину куба. Тогда квадраты, входящие в одну группу, должны быть покрашены в разные цвета, откуда следует, что в каждый цвет должно быть покрашено по 8 квадратов.

4. Имеем цепочку неравенств: a £ h_a £ b £ h_b £ a (первое и третье неравенства следуют из условия задачи, а второе и четвертое – из свойств перпендикуляра и наклонной). Это возможно лишь в том случае, если стороны треугольника равны и перпендикулярны. То есть углы треугольника – 90°, 45°, 45°.

5. Пусть х - искомое число.

1 этап. Меньший – 2 (л). Больший 2х (л)

2 этап. Меньший – 2. Больший 5-2х. И х(5-2х)=2

Откуда х₁=2, х₂=0,5. Таким образом, одна из струй дает вдвое больше воды, чем другая.

6. Пусть a, b, c, d , e – суммы денег, внесенных каждым из друзей, s=a+b+c+d+e – общая стоимость покупки. Предположим, что любые два друга в сумме внесли менее одной трети общей стоимости, то есть , и т.д., всего 10 неравенств. Складывая эти неравенства, получим , что неверно.

7. АМ+МВ>AB, AM+MC>AC, поэтому AM+MB+AM+AC>AB+AC или 2АM+BC>AB+AC, откуда следует утверждение задачи.

9 класс

1. В самом худшем случае будем иметь 9 белых, 9 черных, 9 красных и 10 синих и зеленых – всего 37 шаров. Тогда 38-й шар будет либо белым, либо черным, либо красным и мы получим 10 шаров одного цвета.

2. Смотрите решение задачи 3 для 8 классов.

3. Смотрите решение задачи 6 для 8 классов.

4. При извлечении из этого числа квадратного корня получится .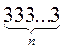

5. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то имеем систему уравнений: Выражаем из первого и второго уравнений а и b через с и подставляем в третье уравнение. Решаем полученное квадратное уравнение и находим с=5, откуда а=3, b=4.

6. Пусть а₁, а₂, а₃, а₄, а₅ – длины данных отрезков, расположенные в порядке возрастания. Если предположить, что утверждение задачи не выполняется, то справедливы три неравенства:

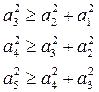
Складывая эти неравенства и приводя подобные члены, получим: . Учитывая а₂³ а₁, а а₃³ а₂ получим отсюда, что , а потому а₅³а₁+а₂. Получили противоречие с неравенством треугольника, что доказывает утверждение задачи.

7. Очевидно, что точки B, C и D не могут лежать на одной прямой. Тогда точка A – точка пересечения высот треугольника BCD.

10 класс

1. Если в урнах одинаковое число шаров, то решение очевидно. Если нет, то удалим из урн шары так, чтобы в одной из них остался один шар. Удвоим число шаров в этой урне и удалим из урн еще по шару. Будем проводить эту операцию до тех пор, пока в урнах не станет по два шара, после чего удалим эти шары.

2. Пусть х – искомое число. Тогда , откуда следует, что 2n²=3m³. Отсюда получаем, что n кратно 3, то есть n=3k и потому 6k²=m³. Минимальное значение k, при котором может выполняться это соотношение, k=6, при этом =18 и х=648.

3. Если все грани многогранника являются треугольниками, то общее число ребер должно делиться на 3. Если же хотя бы в одной из граней вершин больше 3, то общее число ребер не меньше 8.

Смотрите решение задачи 4 для 10 классов.

4. Возведем в квадрат очевидное неравенство (a+b)²£ 2(a²+b²), а затем применим неравенство (a²+b²)²£ 2(a⁴+b⁴) и получим (a+b)⁴£ 4(a²+b²)² £ 8(a⁴+b⁴).

5. Смотрите решение задачи 2 для 11 классов.

6. Через точку М проведем прямую m, параллельную ВС и пересекающую l в точке T, а АВ в точке Е. Очевидно, что TR = ВЕ = 4. Так как треугольник АВМ равнобедренный, то треугольник PMQ тоже равнобедренный, а потому РТ = TR. Обозначим RQ = y, BQ = x. Тогда TQ = 4–y, MQ = 5–x. Из подобия треугольников BRQ и MTQ следует, что y=0,8x. Заметим, что sinÐBQR = sinÐA =0,6.

Тогда S_PMQ+S_BQR= 2S_TMQ+S_BQR=0,6(4-y)(5-x)+0,5×0,6xy=0,6(4-0,8x)(5-x)+0,5×0,6×0,8x² = 0,72x²-4,8x+12. Это выражение достигает минимума, равного 4, при .

7. класс

2. Пусть x_i – число побед i-ой команды, а y_i – число ее поражений. Тогда . Складывая полученные равенства для всех значений i и вынося за скобку общий множитель n–1, получим , так как, очевидно, суммарное количество всех побед равно количеству всех поражений.

3. а) N, M – нечетные. Выигрывает первый. Берет центральную шашку и затем ходит центрально симметрично ходам второго.

б) N или M нечетно. Выигрывает первый. Забирает среднюю горизонталь или вертикаль. И затем повторяет ходы второго симметрично, относительно взятого ряда.

в) N, M – четные. Выигрывает второй. Повторяет ходы первого симметрично относительно центра доски.

4. Пусть точка В расположена между А и С, К – точка пересечения DC с первой окружностью, l – общая касательная к окружностям в точке D. Тогда угол l и AD равен углу DAC, а угол между l и DB равен углу DCB. Отсюда следует, что углы ADK и BDA равны, то есть DA – биссектриса угла BDK, откуда следует утверждение задачи.

5. Очевидно, что x>y. Положим x=y+d, d³1 и подставим в исходное уравнение. Получим (3d-1)y²+(3d²-d)y+d³=61, откуда следует, что d³£61 и d может принимать три значения: 1,2 и 3. Подставляя эти значения в полученное уравнение, найдем его решение: х=6, у=5.

6. 99!=(1×99)×(2×98)×…(49×51)×50< = 50⁹⁹.

7. Проведем через противоположные ребра тетраэдра три пары параллельных плоскостей. Они ограничат параллелепипед, причем ребра тетраэдра будут являться диагоналями граней этого параллелепипеда. Так как противоположные ребра тетраэдра равны, то равны диагонали граней параллелепипеда, то есть этот параллелепипед – прямоугольный. Обозначим через x, y и z его ребра. Тогда 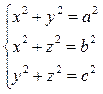Решая эту систему, получим x² = 0,5(a²+b²–c²); y²= 0,5(a²+c²–b²); z² = 0,5(b²+c²–a²). Отсюда имеем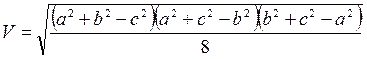

Дата добавления: 2019-01-14; просмотров: 170; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!