Городская математическая олимпиада (2002 год).
С.А.Гулевич
ТВЕРСКИЕ
ГОРОДСКИЕ МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ
Годов
В этот сборниквключенызадачи тверских городских математических олимпиад, проводившихся с 2001 по 2009 года. Большинство из этих задач заимствовано из разных сборников, однако указать автора каждой задачи не представляется возможным. В подборке задач принимали участие преподаватели ТвГУ А.И.Гусев и В.И.Охота а также учителя математики Б.И.Ольшанский, А.А.Сахаров, Г.В.Савенков, С.А. Иванов. Все задачи снабжены решениями, по большей части краткими. Сборник предназначен как для учителей математики, так и для «продвинутых» школьников, желающих самостоятельно готовиться к математическим олимпиадам разного уровня.
ГОРОДСКИЕ МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ
Городская математическая олимпиада (2001 год)
Условия задач.
8 класс.
1. Расшифровать пример на вычитание: летела–стая=ворон
2. Решить уравнение: x2+y2+5=2x+4y
3. Каждое из пяти чисел A, B, C, D, E равно либо 1, либо –1. Разрешается выбрать из них любые три числа и спросить, чему равно их произведение. Как за три вопроса узнать число А?
4. В прямоугольном треугольнике один из углов равен 30°. Доказать, что в этом треугольнике отрезок перпендикуляра, проведенного к гипотенузе через ее середину до пересечения с катетом, втрое меньше этого катета.
5. Обозначим через S(x) сумму цифр числа x. Придумать три натуральных числа a, b, c, для которых S(a+b)<5; S(c+b)<5; S(c+a)<5; S(a+b+c)>50.
|
|
|
6. Найти все целые числа а и b такие, что a4+4b4 является простым числом.
7. В треугольнике АВС медиана ВМ равна высоте АН. Найти угол МВС.
9 класс.
1. Известно, что a>b. Следует ли отсюда, что 4a>3b?
2. Найти 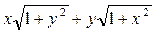 , если
, если 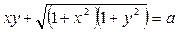 .
.
3. Две окружности О1 и О2 пересекаются в точках А и В, причем их центры расположены вне общей части кругов. Точка С выбрана на окружности О1 произвольно таким образом, чтобы прямые СА и СВ пересекали окружность О2 в точках D и Е, лежащих вне круга О1. Доказать, что длина отрезка DE не зависит от выбора точки С.
4. Решить уравнение 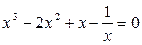
5. В треугольнике АВС медиана ВМ равна высоте АН. Найти угол МВС.
6. В таблице 7´7 выписаны подряд натуральные числа от1 до 49: в первой строке стоят числа 1, 2, 3, 4, 5, 6, 7; во второй – числа 8, 9, 10, 11, 12, 13, 14 и т.д. Выбрали 7 чисел так, что из каждой строки и из каждого столбца выбрано по одному числу. Найти сумму выбранных чисел и доказать, что она не зависит от способа выбора.
7. Число а является корнем уравнения а5–а3+а=2. Доказать, что 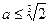 .
.
10 класс.
1. При каком значении а уравнение x2+ax+ôx–1ê+2=0 имеет одно решение?
2. На шахматной доске находится 31 фигура. Докажите, что на этой доске всегда найдется «уголок» из трех клеток, свободный от фигур.
|
|
|
3. Найдите все положительные решения неравенства x2y+xy2+x+y£4xy.
4. Найдите функцию f(x), если при любом значении x выполнено равенство 2f(x)–3f(4–x)=x+1
5. Вне квадрата на его стороне построен прямоугольный треугольник, у которого сторона квадрата является гипотенузой. В каком отношении биссектриса прямого угла этого треугольника делит площадь квадрата?
6. Найдите наибольшее значение выражения 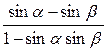 .
.
7. Найдите наибольшее значение выражения x2+y2, если 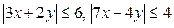 .
.
11 класс.
1. Найдите сумму коэффициентов многочлена (2x–1)100.
2. Решите неравенство 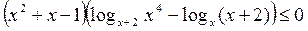
3. Может ли сечение куба плоскостью быть тупоугольным треугольником?
4. Решите уравнение 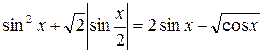
5. Вне квадрата на его стороне построен прямоугольный треугольник, у которого сторона квадрата является гипотенузой. В каком отношении биссектриса прямого угла этого треугольника делит площадь квадрата?
6. Даны три числа. Любые два из них а и b можно заменить на числа 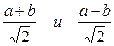 . Можно за несколько таких операций из чисел 2,
. Можно за несколько таких операций из чисел 2, 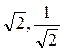 получить числа 1,
получить числа 1, 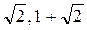 ?
?
7. Докажите, что если уравнение ax2+(c–b)x+(e–d)=0 имеет корень больший 1, то уравнение ax4+bx3+cx2+dx+e=0 имеет хотя бы один корень.
Решения.
8 класс
1. Например, 103017–8372=94645.
2. Переносим все слагаемые в левую часть и, выделяя полные квадраты, приводим уравнение к виду: (x–1)2+(y–2)2=0. Такое возможно лишь при x=1, y=2.
|
|
|
3. Спросим значение чисел ABC, ABD, ACD. Произведение этих чисел A3B2C2D2 равно А, поскольку A2=B2=C2=D2=1.
4. Пусть К – середина гипотенузы АВ прямоугольного треугольника АВС, КМ – отрезок перпендикуляра, проведенного к гипотенузе через точку К до пересечения с катетом АС. По свойству катета, лежащего напротив угла 30°, АМ=2МК. Проведем отрезок МВ. В треугольнике АМВ отрезок МК – высота и медиана, следовательно, АМВ – равнобедренный треугольник и ÐМВК=ÐА=30°. Но тогда и ÐМВС=30°, а потому МС=0,5МВ=0,5МА=МК. Таким образом, АС=АМ+МС=3МК.
5. a=5555554445, b=5554445555, c=4445555555.
6. a4+4b4 = a4+4a2b2+4b4–4a2b2 = (a2+2b2)2–(2ab)2 = (a2+2b2–2ab)(a2+2b2+2ab) = ((a-b)2+b2)((a+b)2+b2). Один из этих множителей должен равняться единице. Так как а и b – целые, то это возможно в одном из следующих случаев:
1) 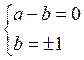 ; 2)
; 2) 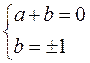 ; 3)
; 3) 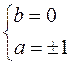
Проверка показывает, что третий случай не удовлетворяет условию задачи (число a4+4b4 не является простым). Таким образом, задача имеет 4 решения: a=b=1; a=b=–1; a=1, b=–1; a=–1, b=1.
7. Достроим треугольник ABC до параллелограмма ABCD. Через точку А проведем прямую, параллельную BD до пересечения с ВС в точке Е. AE=DB=2BM=2AH. Получилось, что в прямоугольном треугольнике АЕН гипотенуза АЕ в два раза больше катета АН, то есть угол АЕН равен 30°. ÐМВС=ÐАЕН=30°.
|
|
|
9 класс
1. Нет. Например, а=–4, b=–5.
2. 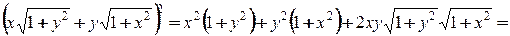
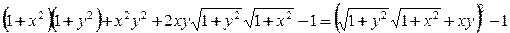
Отсюда следует. что искомое выражение равно 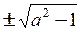 , причем возможны оба случая, поскольку при одновременном изменении знака x и y это выражение меняет знак.
, причем возможны оба случая, поскольку при одновременном изменении знака x и y это выражение меняет знак.
3. ÐDAE не зависит от выбора точки С, поскольку он равен сумме углов ÐACB и ÐAEB, то есть полусумме дуг данных окружностей, заключенных между точками А и В.
4. Данное уравнение приводится к виду (x2+x)2=1 или 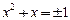 . Уравнение x2+x=-1 корней не имеет, а уравнение x2+x=1 имеет два решения:
. Уравнение x2+x=-1 корней не имеет, а уравнение x2+x=1 имеет два решения: 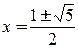 .
.
5. Смотрите решение задачи 7 для 8 класса.
6. Число, стоящее на пересечении k-ой строки и n-го столбца данной таблицы, равно 7(k-1)+n. Вычисляя сумму выбранных чисел, будем отдельно искать сумму первых слагаемых этого разложения и отдельно сумму вторых слагаемых. Из условия задачи следует, что первая сумма равна 7×0+7×1+…+7×6, а вторая сумма равна 1+2+3+4+5+6+7. Общая сумма равна 175.
7. Очевидно, что а>0. Пользуясь неравенством между средним арифметическим и средним геометрическим, получим 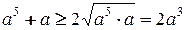 , откуда a5-a3+a ³ a3, т.е 2³а3.
, откуда a5-a3+a ³ a3, т.е 2³а3.
10 класс
1. Перепишем уравнение в виде x2+ax+2 = –÷x-1ç. Нетрудно видеть, что парабола, ветви которой направлены вверх, может иметь с графиком функции y = –÷x-1ç одну общую точку либо в том случае, когда эти графики касаются, либо если вершина ломаной (точка (1;0)) лежит на параболе. Таким образом, мы должны рассмотреть следующие варианты:
1) уравнение x2+ax+2 = –x+1 имеет единственное решение, причем это решение удовлетворяет условию x³1;
2) уравнение x2+ax+2 = x–1 имеет единственное решение, причем это решение удовлетворяет условию x<1;
3) точка (1;0) лежит на параболе y= x2+ax+2.
Исследуя эти варианты, приходим к ответу а1=–3; а2= 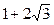 .
.
2. Разобьем шахматную доску на 16 квадратов 2´2. Хотя бы в одном из этих квадратов окажется не более одной фигуры. Но тогда три свободные клетки этого квадрата как раз и составляют уголок.
3. Данное неравенство легко преобразуется к виду x(y–1)2+y(x–1)2£0. Так как x>0, y>0, то полученное неравенство возможно лишь при x=y=1.
4. Так как данное равенство выполняется для всех x, то в нем можно x заменить на 4–х. Получившееся при этом равенство 2f(4-x)–3f(x)=0 вместе с исходным равенством составляет систему относительно f(x) и f(4–x). Решая эту систему, получим f(x)=0,2x-3,4.
5. Рассмотрим окружность, описанную вокруг треугольника. Гипотенуза треугольника будет диаметром этой окружности. Центр квадрата будет лежать на этой окружности, причем он будет делить дугу, опирающуюся на гипотенузу, пополам. Отсюда вытекает, что биссектриса прямого угла проходит через центр квадрата, а потому делит этот квадрат на две равные фигуры.
6. Обозначим sina=a, sinb=b и докажем, что при 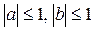 верно неравенство
верно неравенство 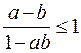 . Перенося 1 в левую часть, приводя к общему знаменателю и раскладывая числитель полученной дроби на множители, мы придем к неравенству
. Перенося 1 в левую часть, приводя к общему знаменателю и раскладывая числитель полученной дроби на множители, мы придем к неравенству 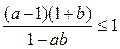 , которое вытекает из наложенных на а и b ограничений. При а=1, b=0 исходное выражение принимает значение 1, таким образом 1 – это его максимальное значение.
, которое вытекает из наложенных на а и b ограничений. При а=1, b=0 исходное выражение принимает значение 1, таким образом 1 – это его максимальное значение.
7. Раскрывая модули, получим систему неравенств 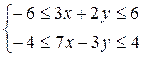 Эта система определяет параллелограмм с центром в начале координат. Так как величина x2+y2 – это квадрат расстояния от начала координат до точки (x;y), то для решения задачи нам надо найти внутри параллелограмма или на его границе точку, максимально удаленную от начала координат. Очевидно, что искомой точкой будет одна из вершин параллелограмма. В силу симметрии достаточно рассмотреть две смежные вершины, которые можно найти, решая системы:
Эта система определяет параллелограмм с центром в начале координат. Так как величина x2+y2 – это квадрат расстояния от начала координат до точки (x;y), то для решения задачи нам надо найти внутри параллелограмма или на его границе точку, максимально удаленную от начала координат. Очевидно, что искомой точкой будет одна из вершин параллелограмма. В силу симметрии достаточно рассмотреть две смежные вершины, которые можно найти, решая системы: 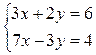 и
и 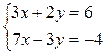 Из первой системы получаем точку
Из первой системы получаем точку 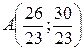 , из второй – точку
, из второй – точку 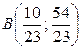 . Вычисляя для этих точек величину x2+y2, определим ее максимальное значение, равное
. Вычисляя для этих точек величину x2+y2, определим ее максимальное значение, равное 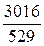 .
.
11 класс
1. Сумма коэффициентов многочлена равна, очевидно, значению этого многочлена при х=1. В данном случае это значение равно 1.
2. Функция, стоящая в левой части неравенства определена при x>0, x¹1 и обращается в 0 при х=2 и 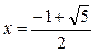 . Применяя метод интервалов, получим, что данное неравенство верно при
. Применяя метод интервалов, получим, что данное неравенство верно при 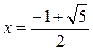 и при 1<x£2.
и при 1<x£2.
3. Нет. Сечение будет треугольником, если секущая плоскость пересекает три ребра, выходящие из одной вершины куба, например А. Пусть X, Y, Z – вершины этого треугольника. Обозначим AX=x, AY=y, AZ=z. Тогда по теореме Пифагора квадраты сторон треугольника будут равны x2+y2, x2+z2 и y2+z2, откуда следует, что сумма квадратов двух сторон треугольника XYZ всегда будет больше квадрата третьей стороны, т.е. этот треугольник остроугольный.
4. Данное уравнение приведем к виду 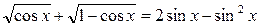 . Левая часть этого уравнения не может быть меньше 1, в чем легко убедиться, возводя ее в квадрат. С другой стороны, правая часть уравнения – квадратный трехчлен относительно sinx, вершина которого находится в точке (1;1), а ветви направлены вниз. То есть его значение не может быть больше 1. Таким образом, наше уравнение равносильно системе
. Левая часть этого уравнения не может быть меньше 1, в чем легко убедиться, возводя ее в квадрат. С другой стороны, правая часть уравнения – квадратный трехчлен относительно sinx, вершина которого находится в точке (1;1), а ветви направлены вниз. То есть его значение не может быть больше 1. Таким образом, наше уравнение равносильно системе 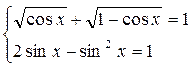 , решая которую, получим
, решая которую, получим 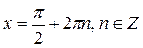
5. См. решение задачи 5 из 10-го класса.
6. Нет, так как сумма квадратов исходных чисел при заданной операции не меняется, а для указанных троек чисел эта сумма различна.
7. Пусть уравнение ax2+(c–b)x+(e–d)=0 имеет корень t2>1. Тогда at4+(c-b)t2+(e-d)=0 или at4+ct2+e = bt2+d. Рассмотрим функцию f(x)= ax4+bx3+cx2+dx+e и сосчитаем ее значения в точках t и -t. В силу доказанного выше f(t)= (at4+ct2+e) +t(bt2+d) = (t+1)(bt2+d); f(-t)= (at4+ct2+e) – t(bt2+d) = (1–t)(bt2+d). Так как t>1, то f(t) и f(-t) имеют разные знаки. Отсюда следует, что многочлен f(x) имеет хотя бы один корень.
городская математическая олимпиада (2002 год).
Условия задач
8 класс
1. При каких х, y , z имеет место равенство: 4х2 + 9у2 + 16z2 – 4х – 6 у– 8z = 0?
2. Докажите, что значение выражения 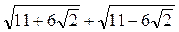 является натуральным числом.
является натуральным числом.
3. В банке лежат 1995 белых и 1996 черных зерен. Наугад достают 2 зерна. Если они одного цвета, то зерна выбрасывают, а в банку кладут черное зерно. Если зерна разного цвета, то черное выбрасываем, а белое кладем обратно. В конце концов в банке останется 1 зерно. Какого оно цвета?
4. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса CD. Из точки D восставлен перпендикуляр DF к прямой DC (точка F лежит на АС) и проведена прямая DEúêAC (точка Е лежит на ВС). Биссектриса угла В пересекает прямую DE в точке М. Доказать, что FC = 4DM.
5. Найти зависимость между a , b , c , если а = х + у; b = x2 + y2; c = x3 + y3.
6. Имеется 77 шариков одного и того же радиуса, один из них легче всех остальных. Найти его с помощью 4 взвешиваний на чашечных весах (без гирь).
7. Можно ли прямоугольник размером 55´39 разрезать на прямоугольники размером 5´11?
9 класс
1. См. задачу 2 для 9 классов.
2. Дописать к числу 523 справа три цифры так, чтобы полученное число делилось на 7, 8 и 9.
3. Можно ли в круге радиуса 2 разместить 8 непересекающихся квадратов со стороной 1?
4. 10 человек пришли в гости в галошах. Уходили они по одному, и каждый надевал произвольную пару галош, в которую смог влезть (т.е. не меньшего размера, чем его собственная). Каким может оказаться наибольшее число людей, которые не смогли надеть галоши?
5. Найти двузначное число, которое равно сумме куба числа десятков и квадрата числа единиц.
6. Сколько корней имеет уравнение 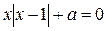 ?
?
7. Разделить отрезок на две равные части, используя трафарет в виде полукруга.
10 класс
1. Может ли в сечении куба плоскостью получиться неравнобедренная трапеция?
2. Докажите, что уравнение 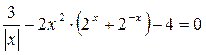 не может иметь нечетное число корней.
не может иметь нечетное число корней.
3. Найти наименьшее натуральное число, начиная с которого 2002 последовательных натуральных числа не являются точными квадратами.
4. Докажите, что система 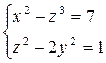 не имеет целочисленных решений.
не имеет целочисленных решений.
5. В треугольнике АВС проведены высота ВН и биссектриса АЕ. Угол АЕВ равен 45о. Найти угол ЕНС.
6. Доказать, что tg3o45’ – иррациональное число.
7. Разделить на три равные части отрезок с помощью односторонней линейки и трафарета в виде полукруга.
11 класс
1. Доказать, что для всех x верно неравенство х6+х5+х4+х3+х2+х+1>0.
2. Докажите, что уравнение 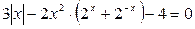 не может иметь нечетное число корней.
не может иметь нечетное число корней.
3. Найти расстояние между скрещивающимися диагоналями двух соседних граней единичного куба.
4. В равнобедренную трапецию ABCD с основаниями AD и ВС вписана окружность. М – точка касания окружности со стороной DC, Н и К – точки пересечения окружности с отрезками ВМ и АМ соответственно. Найти 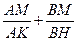 .
.
5. Решить систему уравнений 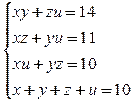
6. Доказать, что при 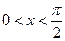 справедливо неравенство
справедливо неравенство 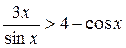 .
.
7. Решить уравнение 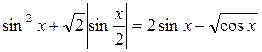
Решения
8 класс
1. Выделяя полные квадраты, получим (2х–1)2+(3у–1)2+(4z–1)2 = 0, откуда 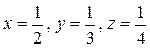 .
.
2. При возведении данного выражения в квадрат получим 49, откуда следует, что значение этого выражения равно 7.
3. Если берут два белых зерна, то вместо них кладут черное, при этом количество белых зерен уменьшается на 2. Если берут два черных зерна, то количество белых зерен не меняется. Если берут зерна разного цвета, то количество белых зерен также не меняется. Отсюда видно, что количество белых зерен всегда остается нечетным, то есть последнее зерно в банке должно быть белым.
4. Продолжим FD до пересечения с прямой ВС в точке К. В треугольнике СFK отрезок CD является высотой и биссектрисой, а, следовательно, и медианой. Поэтому DF=DK и DE – средняя линия треугольника СFK. То есть FC=2DE. Так как, в свою очередь, DE=2DM, то FC=4DM.
5. ( x + y )3= x 3 + y 3 +3 xy ( x + y ), то есть a 3 = c +3 xya . Но 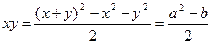 , откуда получаем 2 a 3 =2 c +3 a 3 –3 ab или a 3 +2 c =3 ab .
, откуда получаем 2 a 3 =2 c +3 a 3 –3 ab или a 3 +2 c =3 ab .
6. Положим на обе чашки по 27 шариков. Этим мы определяем, в какой группе находится искомый шарик. Если он находится среди 23 оставшихся на столе, то добавим к ним 4 шарика, сведя задачу к исследованию группы из 27 шариков. Для решения этой задачи положим на каждую чашку весов по 9 шариков и определим группу из 9 шариков, в которой находится искомый. Далее взвешиваем по три шарика, а потом по одному.
7. Нет, так как уравнение 5n+11m = 39 не имеет решений в натуральных числах ( убедиться в этом можно перебором).
9 класс
1. См. решение задачи 2 за 8 класс.
2. Чтобы число делилось на 7, 8 и 9 необходимо и достаточно, чтобы оно делилось на произведение этих чисел, то есть на число 504. Приписать к числу 523 справа три цифры – это то же самое, что прибавить к числу 523000 трехзначное число, составленное из этих цифр. Число 523000 дает при делении на 504 остаток 352. Добавим к нему 504–352=152 и получим число, которое делится на 504 без остатка. У задачи имеется второй ответ: 656.
3.
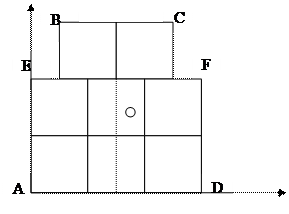 |
Расположим квадраты так, как показано на рисунке и докажем, что радиус описанной вокруг трапеции ABCD окружности меньше 2, а точки E и F лежат внутри этой окружности.
Введем систему координат с началом в точке А и осями AD и АЕ. Тогда точка В имеет координаты (0,5;3). Пускай О(1,5;y) – центр описанной вокруг трапеции ABCD окружности. Так как ОА2 = ОВ2, то 2,25+у2=1+(3–у)2, откуда 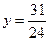 Находим теперь радиус окружности и убеждаемся, что он меньше 2. То же относится и к длине отрезка ОЕ.
Находим теперь радиус окружности и убеждаемся, что он меньше 2. То же относится и к длине отрезка ОЕ.
4. Если пять маленьких гостей наденут пять больших галош, то оставшиеся гости окажутся без галош. Шесть человек без галош остаться не могут, так как из любых шести человек можно выбрать самого маленького – для него имеется 6 подходящих пар галош, и гости, ушедшие перед ним, не смогут их все забрать, поскольку таких гостей лишь четверо.
5. у2–у = 10х–х3 = х(10–х2), откуда следует, что х – четное число, квадрат которого не превосходит 10, то есть х = 2. Решая квадратное уравнение, получаем у = 4.
6. Решим задачу графически. Для этого построим графики функций 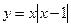 и у = –а.
и у = –а.
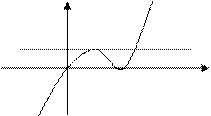 |
По графику легко определить, что одно решение уравнение имеет, если a>0 или a<–0,25; два решения – если a = 0 или a = –0,25; три решения – если –0,25<a<0.
7. Будем откладывать трафарет от левого и правого концов отрезка до тех пор, пока k-ый слева контур трафарета не пересечет k-ый справа контур. Проделаем эту операцию дважды – сверху и снизу от отрезка. Соединим отрезком (диаметром трафарета) две получившиеся у нас точки пересечения.
 |  | ||
Если в отрезке укладывается целиком нечетное число трафаретов, то нам придется научиться находить середину диаметра трафарета. Для этого обведем трафарет, повернем вдоль получившейся дуги и еще раз обведем. Точка пересечения двух нарисованных при этом отрезков и будет серединой диаметра.
10 класс
1. Да, такое сечение провести можно. Возьмем, например, в кубе ABCDA1B1C1D1 на ребре ВС точку М так, что ВМ:МС=1:3, а на ребре A1B1 точку Р так, что А1Р = РВ1. Плоскость, проходящая через точки А, М и Р пересечет ребро B1C1 в точке К такой, что В1К:КС1=1:7. То есть сечением будет неравнобедренная трапеция АМКР.
2. Решениями данного уравнения являются нули четной функции. Так как число х=0 не является корнем уравнения, то количество корней должно быть четным.
3. Для решения задачи достаточно найти такое натуральное число n, что между числами n2 и (n+1)2 заключено 2002 натуральных числа. То есть (n+1)2–n2–1=2002. Это равенство выполняется при n=1001. Значит первым числом в искомой серии будет число 10012+1.
4. Из второго уравнения следует, что число z является нечетным, т.е. z=2k+1, откуда (2k+1)2–2y2=1. Раскрыв скобки, получим 4k2+4k–2y2=0, то есть у – четное число. Воспользовавшись первым уравнением, получим , что х – число нечетное. То есть у=2n, а x=2m+1. Подставив эти выражения в первое уравнение, получим 4m2+4m–8n3=6, чего быть не может, поскольку левая часть этого уравнения делится на 4, а правая не делится.
5. Построим точку В1, симметричную точке В относительно прямой АЕ. Так как АЕ – биссектриса угла ВАС, то точка В1 лежит на прямой АС. Так как угол ВЕА = 45о, то угол ВЕВ1 – прямой. Так как угол ВНВ1 тоже прямой, то вокруг четырехугольника ВНВ1Е можно описать окружность. Так как ВЕ = В1Е, то равны углы ВНЕ и ЕНВ1 (вписанные углы, опирающиеся на равные хорды). Но эти углы в сумме составляют прямой угол, то есть каждый из них равен 45о. Получили, что ÐЕНС = 45о.
6. Если tg3o45’ рациональное число, то, трижды применяя формулу тангенса двойного угла, получим, что рациональным числом является 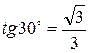 . Противоречие.
. Противоречие.
7. Используя одностороннюю линейку и шаблон, нетрудно построить треугольник, в котором данный отрезок будет медианой. Используя способ, описанный в задаче 7 для 9 классов, проведем в этом треугольнике вторую медиану, которая разделит данный отрезок в отношении 2:1. Осталось больший из полученных отрезков разделить пополам.
11 классы.
1. Проще всего для решения этой задачи воспользоваться формулой для суммы геометрической прогрессии, согласно которой данное выражение равно 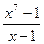 (случай х=1 надо рассмотреть отдельно). В полученной дроби числитель и знаменатель имеют одинаковые знаки, откуда следует, что эта дробь положительна.
(случай х=1 надо рассмотреть отдельно). В полученной дроби числитель и знаменатель имеют одинаковые знаки, откуда следует, что эта дробь положительна.
2. См. решение задачи 2 для 10 классов.
3. Стандартная задача на применение метода координат. Введем для куба ABCDA1B1C1D1 систему координат так, что точка В совпадет с началом координат, а точки А, С и В1 будут расположены на осях ОХ, ОY и OZ соответственно. Пусть точка М лежит на диагонали АВ1, а точка N – на диагонали BD. Тогда М(х;0; 1–х), N(y; y; 0), 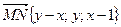 ,
, 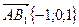 ,
, 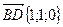 . Отрезок MN задает расстояние между скрещивающимися прямыми АВ1 и BD в том случае, когда он перпендикулярен каждой из них. Это означает равенство нулю скалярного произведения соответствующих векторов. То есть имеет место система уравнений
. Отрезок MN задает расстояние между скрещивающимися прямыми АВ1 и BD в том случае, когда он перпендикулярен каждой из них. Это означает равенство нулю скалярного произведения соответствующих векторов. То есть имеет место система уравнений 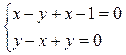 , решив которую, получим
, решив которую, получим 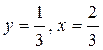 . Откуда следует, что длина отрезка MN, задающего расстояние между скрещивающимися прямыми АВ1 и BD, равна
. Откуда следует, что длина отрезка MN, задающего расстояние между скрещивающимися прямыми АВ1 и BD, равна 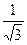 .
.
4. Пусть АМ = у, АК = х, AF = DF = DM = a, ÐADM=a. По теореме о касательной и секущей а2 = ху. По теореме косинусов для треугольника AMD y2 = a2+4a2–4a2cosa = a2(5–4cosa) = xy(5–4cosa). То есть 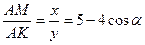 . Аналогично доказывается (учитывая, что ÐВСМ = 180о–a) равенство
. Аналогично доказывается (учитывая, что ÐВСМ = 180о–a) равенство 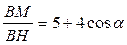 . Складывая два доказанных равенства получаем, что искомая сумма равна 10.
. Складывая два доказанных равенства получаем, что искомая сумма равна 10.
5. 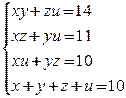 Сложив первое уравнение со вторым, получим ( x + u )( y + z ) = 25. Учитывая четвертое уравнение, найдем x + u = y + z = 5. Сложим теперь первое уравнение с третьим, и, учитывая четвертое уравнение, получим
Сложив первое уравнение со вторым, получим ( x + u )( y + z ) = 25. Учитывая четвертое уравнение, найдем x + u = y + z = 5. Сложим теперь первое уравнение с третьим, и, учитывая четвертое уравнение, получим 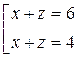 . Складывая второе уравнение с третьим, найдем
. Складывая второе уравнение с третьим, найдем 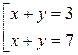 . Осталось рассмотреть 4 варианта:
. Осталось рассмотреть 4 варианта: 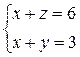 ;
; 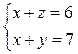 ;
; 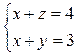 и
и 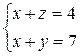 . Учитывая, что x+u = y+z = 5, получим 4 решения исходной системы: (2;1;4;3), (1;2;3;4), (3;4;1;2), (4;3;2;1).
. Учитывая, что x+u = y+z = 5, получим 4 решения исходной системы: (2;1;4;3), (1;2;3;4), (3;4;1;2), (4;3;2;1).
6. Так как при указанных ограничениях sinx>0, то данное неравенство равносильно неравенству 3x>4sinx–0,5sin2x. Для доказательства этого неравенства проведем исследование функции y = 3x –4sinx+0,5sin2x с помощью производной. y ' = 3 – 4cosx + cos2x = 2(1–cosx)2. То есть данная функция является возрастающей на всей числовой прямой. Так как у(0)=0, то при указанных значениях х справедливо неравенство 3x –4sinx+0,5sin2x > 0, что и требовалось доказать.
7. Данное уравнение преобразуем к виду 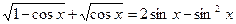 и оценим его левую и правую части.
и оценим его левую и правую части.
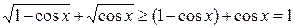 (т.к. 0 £ a £ 1 Þ
(т.к. 0 £ a £ 1 Þ 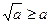 )
)
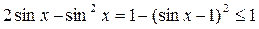
Отсюда следует, что обе части уравнения равны 1. Это возможно лишь в случае, когда sinx = 1, т.е. 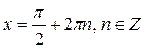
Дата добавления: 2019-01-14; просмотров: 209; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
