Городская математическая олимпиада (2008 год)
Условия задач
8 класс
1. Постройте график функции 
.
2. Докажите, что число 
делится на 7.
3. Известно, что в десятичной записи числа 229 участвует ровно 9 цифр, и все эти цифры различны. Докажите, что среди этих цифр есть 0.
4. Каждую сторону некоторого прямоугольника увеличили на 3см, в результате чего его площадь увеличилась на 39 см2. Найти периметр прямоугольника.
5. Найдите два числа, сумма, произведение и частное которых равны между собой.
9 класс
1. Постройте график функции 
.
2. Докажите, что в последовательности чисел 1, 11, 111, … найдется число, которое делится на 2009.
3. В треугольнике АВС угол В равен 60˚, биссектрисы АК и СЕ пересекаются в точке О. Найти углы треугольника ЕКО.
4. Взяли натуральное число, затем вычли из него число, записанное теми же цифрами, но в другом порядке, и в полученном числе зачеркнули одну цифру. Сумма оставшихся цифр равна 29. Какую цифру зачеркнули?
5. Рассматриваются квадратные трехчлены вида x2+px+q с целыми коэффициентами, при этом p+q=30. Сколько таких многочленов имеют целые корни?
10 класс
1. Найдите какое-нибудь натуральное число, которое само делится на 2008 и сумма его цифр тоже делится на 2008.
2. Два одинаковых выпуклых четырехугольника разрезали: один по одной диагонали, а другой – по другой диагонали. Докажите, что из этих четырех частей можно сложить параллелограмм.
3. Какое наибольшее число белых и чёрных фишек можно расставить на шахматной доске так, чтобы на любой горизонтали и на любой вертикали белых фишек было ровно в два раза больше, чем чёрных? (Каждая фишка занимает отдельную клетку).
|
|
|
4. Рассматриваются квадратные трехчлены вида x2+px+q с целыми коэффициентами, при этом p+q=30. Сколько таких многочленов имеют целые корни?
5. Определенная на множестве действительных чисел функция f(x) такова, что для любого х выполнено равенство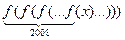 
= 1. Докажите, что уравнение f(x) = 1 имеет не менее двух корней.
11 класс.
1. Докажите, что сумма n последовательных натуральных чисел делится на n, если n нечетно.
2. В клетках квадратной таблицы 10х10 произвольным образом расставлены числа от 1 до 100. Может ли оказаться так, что суммы чисел, стоящих в двух соседних строках таблицы, отличаются ровно на 1?
3. Плоскость пересекает стороны АВ, ВС, CD и DA пространственного четырехугольника ABCD в точках K, L, M, N соответственно. Докажите что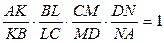 
.
4. Докажите, что существует 2008 идущих подряд составных натуральных чисел.
5. На бумажке записано число 1 и некоторое нецелое число x. За один ход разрешается записать на бумажку сумму или разность каких-нибудь двух уже записанных чисел или записать число, обратное к какому-нибудь из уже записанных чисел. Можно ли за несколько ходов получить на бумажке число x2?
|
|
|
Решения.
8 класс
1. Область определения данной функции – множество чисел, удовлетворяющих двойному неравенству 
. При выполнении этих условий y = 1–x+1+x = 2. Графиком этой функции будет отрезок, соединяющий точки (–1;2) и (1;2) координатной плоскости.
2. Для решения задачи достаточно доказать, что на 7 делится число, составленное из 2010 девяток, а для этого надо проверить, что 102010 при делении на 7 дает остаток 1. Чтобы доказать этот факт, найдем остатки от деления на 7 чисел вида 10n. Вот последовательность этих остатков: 3, 2, 6, 4, 5, 1, 3, после чего остатки начинают повторяться. Таким образом, остаток 1 получается, когда n= 6, 12, 18, … и вообще при любом n, кратном 6. Поскольку 2010 делится на 6, то 102010 при делении на 7 тоже дает остаток 1.
3. Если среди этих цифр нет цифры 0, то это число должно быть записано цифрами 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако сумма этих цифр делится на 9, то есть и само число должно делиться на 9. Однако число 229 на 9 не делится.
4. Пусть х и у – стороны прямоугольника, тогда (х+3)(у+3) – ху = 39. Раскрывая скобки и приводя подобные члены, получим 3х+3у = 30, откуда х+у = 10, то есть периметр прямоугольника равен 20 см.
|
|
|
5. Пусть х и у – эти числа. Тогда х+у = ху = х:у. Очевидно, что х не равно 0. Тогда из второго равенства получим, что у2 = 1. При у = 1 система решений не имеет, рассмотрим случай у = –1. Тогда х–1 = –х, то есть х = 0,5. Итак, получили, что х = 0,5; у = –1.
9 класс
1. Область определения данной функции – множество чисел, удовлетворяющих двойному неравенству . При выполнении этих условий у = 1–х2. Графиком этой функции будет участок параболы у = 1–х2, заключенный между точками (–1;0) и (1;0).
2. Возьмем 2010 чисел указанного вида и рассмотрим их остатки от деления на 2009. Так как всего существует 2009 разных остатков от деления на 2009 (включая число 0), то найдется два числа, имеющих одинаковые остатки. Разность этих чисел делится на 2009, но эта разность имеет вид 111…11000…00, то есть может быть записана как число 111…11, умноженное на 10n. Но 10n не имеет с числом 2009 общих делителей, а потому 111…11 должно делиться на 2009.
3. 
. Отсюда следует, что вокруг четырехугольника ВКОЕ можно описать окружность. По свойству вписанных углов опирающихся на одну дугу имеем 
. Но ВО – биссектриса, поэтому 
, откуда следует что 
.
4. Известно, что любое число при делении на 9 дает такой же остаток, как и сумма его цифр. Это означает, что любое число и число, записанное теми же цифрами, но в другом порядке, дают при делении на 9 одинаковый остаток. Но тогда разность их делится на 9, и сумма цифр этой разности тоже делится на 9. Таким образом, если к 29 прибавить зачеркнутую цифру, то получится число, которое делится на 9. Это может быть только в том случае, если была зачеркнута цифра 7.
|
|
|
5. Пусть х1 и х2 корни трехчлена x2+px+q. Пусть для определенности х1>x2. Тогда по теореме Виета х1 + х2 = –р, х1·х2 = q, откуда получим, что х1·х2 – х1 – х2 = 30. Данное равенство легко преобразовать к виду (х1–1)(х2–1) = 31. Так как 31 – простое число, то существуют две пары корней, удовлетворяющих этому уравнению: (32;2) и (–30; 0). Таким образом, существуют два многочлена указанного вида с целочисленными корнями.
10 класс
1. Например, число 200820082008…2008 (2008 раз).
2. Пусть ABCD и A1B1C1D1 – эти четырехугольники. Разрежем первый по диагонали BD, а второй – по диагонали А1С1 и приложим отрезок AD к отрезку D1A1 (вершина А к вершине D1), затем отрезок А1В1 приложим к отрезку ВА (вершина В1 к вершине А) и, в конце концов, отрезок ВС приставим к отрезку С1В1. При этом отрезок CD соединится с отрезком D1C1. Мы получили четырехугольник, стороны которого являются диагоналями исходных четырехугольников, причем противоположные стороны равны, а, значит, полученный четырехугольник – параллелограмм.
3. Очевидно, что ни на одной горизонтали не может быть больше 2 черных фишек, а потому общее число черных фишек не может превосходить 16, а белых, соответственно, 32. В тоже время расстановка с 16 черными и 32 белыми фишками существует, например:
| ч | б | б | б | б | ч | ||
| ч | ч | б | б | б | б | ||
| ч | ч | б | б | б | б | ||
| ч | ч | б | б | б | б | ||
| б | ч | ч | б | б | б | ||
| б | б | ч | ч | б | б | ||
| б | б | б | ч | ч | б | ||
| б | б | б | б | ч | ч |
4. Смотрите решение задачи 5 для 9 классов.
5. Одно из решений этого уравнения x=1. Действительно, по условию задачи 
. Чтобы найти второй корень рассмотрим любое число 
и положим x1=f(x0), x2=f(x1) и так далее. Из условия следует, что x2008=1. Пусть xn – первый член последовательности, равный единице. Тогда xn-1 – корень уравнения f(x) = 1.
11 класс
1. Рассмотрим числа k, k+1, k+2,…k + n–1. Их сумма равна 
. Если n нечетное, то 2k+n–1 четное, а потому 
целое, то есть сумма чисел делится на n.
2. Нет. Действительно, предположим, что требуемая расстановка чисел существует. Тогда суммы чисел, стоящих в соседних строках, имеют разную четность. Это означает, что пять таких сумм будут четными, а пять – нечетными. Но тогда сумма всех записанных в таблице чисел будет нечетным числом. Однако сумма натуральных чисел от 1 до 100 равна 5050, то есть является числом четным. Противоречие.
3. Пусть h1, h2, h3 и h4 – расстояния от точек А, В, С и D до данной плоскости. Тогда указанное в условии задачи произведение равно 
.
4. Рассмотрим числа 2009!+2, 2009!+3, … , 2009!+2009. Первое из них делится на 2, второе делится на 3, третье делится на 4 и так далее. (Здесь n! – произведение натуральных чисел от 1 до n).
5. Можно. Заметим, что из любого числа у легко получить число (у+1)+(у–1) = 2у. Для решения задачи из числа (х–1)–1 вычтем число (х+1)–1, к полученному результату возьмем обратное число, которое умножим на 2 (смотрите замечание), после чего прибавим 1.
Дата добавления: 2019-01-14; просмотров: 250; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!