Городская математическая олимпиада (2003 год).
Условия задач.
8 класс
1. Докажите, что (3а+5b+7)5(5а+3b+6)7 делится на 32 при любых целых а и b.
2. На какое максимальное количество нулей может оканчиваться произведение трех натуральных чисел, сумма которых равна 407?
3. Я втрое моложе моего учителя, сумма цифр моего возраста на 1 меньше суммы цифр возраста моего учителя, а разность цифр моего возраста на 1 больше разности цифр возраста моего учителя. Сколько лет мне и сколько моему учителю?
4. В выпуклом четырехугольнике ABCD проведены диагонали. При этом оказалось, что ÐВАС = ÐСВD, а ÐACD = ÐBDA. Доказать, что ÐАВС = ÐADС.
5. Сто монет разложили в 10 стопок по 10 монет в каждой. В одной из стопок все монеты фальшивые. Масса каждой настоящей монеты 5 граммов, а масса фальшивой – на 0,5 грамма меньше. Как с помощью одного взвешивания на весах с разновесами определить, в какой стопке находятся фальшивые монеты?
6. Определить, при каких х число х4 + 4 будет простым.
7. На острове Тузла 
всех мужчин женаты и 0,6 всех женщин замужем. Какая часть взрослого населения острова состоит в браке?
9 класс
1. Докажите, что (3а+5b+7)5(5а+3b+5)7 делится на 32 при любых целых а и b.
2. На острове Тузла 
всех мужчин женаты и 0,6 всех женщин замужем. Какая часть взрослого населения острова состоит в браке?
3. Пусть а, b , c – стороны треугольника. Докажите неравенство а3 + b3 + 3abc > c3.
4. Катер, плывя вверх по реке, потерял под мостом бутылку. Обнаружив потерю через 10 минут, катер повернул назад и догнал бутылку в 1 километре от моста. Найдите скорость реки.
|
|
|
5. Из числа, записанного 2n единицами, вычли число, записанное n двойками. Докажите, что полученное число является квадратом целого числа.
6. Произведение 25 натуральных чисел оканчивается на 25. Доказать, что среди них найдутся три числа, произведение которых оканчивается на 25.
7. Можно ли пятиконечную звезду разрезать на 3 выпуклых многоугольника?
10 класс
1. Какой цифрой оканчивается сумма 20032004+20042003.
2. Построить график функции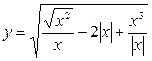 
.
3. Какое число больше: 99! или 5099?
4. В выпуклом четырехугольнике ABCD точки Е и К являются серединами сторон ВС и CD соответственно. Отрезки АЕ, АК и ЕК делят четырехугольник на 4 треугольника, площади которых равны последовательным натуральным числам. Какие значения может принимать площадь треугольника ABD?
5. Докажите, что ни одно из чисел 11, 111, 1111, 11111, … не является квадратом целого числа.
6. На плоскости дано 999 точек. Известно, что среди любых трех из них имеются две, расстояние между которыми не больше 1. Докажите, что на плоскость можно положить два круга радиуса 1, которые закроют все точки.
7. Четыре трехзначных числа, начинающихся с одной цифры, обладают тем свойством, что их сумма делится на некоторые три из этих чисел. Найти эти числа.
|
|
|
11 класс
1. Что больше: cos(cos1) или cos1?
2. Числа a, b, c удовлетворяют условиям: a+b+c > 0; b2 < 4ac. Доказать, что числа а и с положительны.
3. Решите уравнение в целых числах 19х + 9у = (19 +х)(9 + у).
4. Решить систему уравнений 
5. Найдите углы равнобедренного треугольника, у которого точка пересечения высот лежит на вписанной окружности.
6. Докажите, что проекция правильного тетраэдра на плоскость имеет наибольшую площадь, если эта плоскость параллельна скрещивающимся ребрам тетраэдра
7. Найти все решения уравнения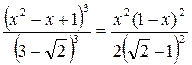 
.
Решения.
8 класс
1. Если числа а и b оба четные или оба нечетные, то 5а+3b+6 делится на 2, а потому седьмая степень этого выражения делится на 32. Если же а и b разной четности, то четным является число 3а+5b+7, то есть его пятая степень делится на 32.
2. 6 нулей. Больше шести нулей получиться не может, поскольку только два числа из трех могут делиться на 5, а так как все слагаемые должны быть меньше 54 = 625, то множитель 5 в произведении этих чисел будет встречаться не более 6 раз. С другой стороны, 407 = 125 + 32 + 250, а 125×32×250 = 1000000.
3. Пусть х и у – цифры моего возраста, а и b – цифры возраста моего учителя (x>y; а>b). Тогда x+y = a+b–1; x–y = a–b+1. Складывая эти уравнения, получим x = a, потому y = b–1. Теперь надо рассмотреть 4 варианта: 1) 3(10x+y) = 10a+b; 2) 3(10x+y) = 10b+a; 3) 3(10y+x) = 10a+b; 4) 3(10y+x) = 10b+a. Учитывая полученные ранее соотношения, будем иметь: 1) 30a+3b–3 = 10a+b; 2) 30a+3b–3 = 10b+a; 3) 30b–30+3a = 10a+b; 4) 30b–30+3a = 10b+a. Первый случай, очевидно, невозможен. Во втором случае 29а = 7b+3. Так как b<9, то a может принимать значения 1 и 2. Непосредственной проверкой убеждаемся, что оба этих значения не подходят. В третьем случае 29b = 7a+30. В этом случае b£3. Проверяя эти значения, находим решение: b=2; a=4. В четвертом случае 20b+2a=30. Это возможно при b = 1; a = 5. Но в этом случае получается, что мой возраст равен 5, а по условию задачи возраст должен выражаться двузначным числом. Таким образом имеем ответ6 14 и 42.
|
|
|
4. Обозначим через О точку пересечения диагоналей четырехугольника. По условию ÐВАС = ÐСВD, а ÐACD = ÐBDA. Углы АОВ и COD равны как вертикальные. ÐАВО = 180° – ÐВАС – ÐАОВ, ÐBDC = 180° – ÐАСD – ÐCOD, поэтому ÐАВС = 180° – ÐВАС – ÐАОВ + ÐСВD = 180° – ÐАОВ, а ÐADС = ÐBDC = 180° – ÐАСD – ÐCOD + ÐBDA = 180° – ÐCOD. Из равенства углов следует утверждение задачи.
5. Из первой стопки возьмем 1 монету, из второй – две, из третьей – три и так далее, всего 55 монет. Затем одним взвешиванием определим суммарный вес взятых монет. Если полученное число на 0,5 грамма отличается от 275 граммов (вес 55 настоящих монет), то имеется одна фальшивая монета, а, значит, фальшивые монеты лежат в первой стопке. Если разница в весе составляет 1 грамм, то фальшивых монет 2, то есть они взяты из второй стопки. То есть номер стопки с фальшивыми монетами равен удвоенной разнице между 275 граммами и весом взятых монет.
|
|
|
6. х4+4 = х4+4х2+4–4х2 = (х2+2)2–(2х)2 = (х2+2-2х)(х2+2+2х). Чтобы это число было простым, один из множителей должен равняться 1 (нетрудно показать, что оба множителя положительны). Это происходит при х = ±1.
7. Пускай на острове х семейных пар, то есть х женатых мужчин и х замужних женщин. Тогда общее количество живущих на острове мужчин равно 
, а женщин - 
. То есть взрослое население острова составляет 
человек, из которых 2х человек состоят в браке. Таким образом, доля состоящих в браке среди всего взрослого населения равна 
.
9 класс.
1. Смотрите 8.1
2. Смотрите 8.7
3. а3 + b3 + 3abc = (а+b)(a2-ab+b2)+3abc > c(a2-ab+b2)+3abc = c(a2+2abc+b2) = c(a+b)2 > c3.
4. Так как скорость катера относительно бутылки не зависит от того, плывет ли он по течению или против, то, обнаружив потерю через 10 минут, катер догонит бутылку еще через 10 минут. То есть за 20 минут бутылка проплыла 1 км, а потому скорость течения равна 3км/час.
5. Обозначим через х число, записанное n единицами. Заметим, что 9х+1 = 10n, то есть 
. Тогда число, записанное 2n единицами, равно х×10n + x, а число, записанное n двойками, равно 2х. То есть интересующая нас разность равна х(10n–1) = 
.
6. Раз произведение всех чисел оканчивается на 25, то оно делится на 25. То есть можно выбрать два таких множителя х и у, произведение которых делится на 25 (либо каждый из них делится на 5, либо один из них делится на 25). Остальные множители, очевидно, нечетные числа. Проследим, как меняются две последние цифры произведения х×у при умножении на нечетное число. Умножая х×у на число вида 4n+1 мы не меняем две последние цифры, умножая на число вида 4n+3, мы меняем 75 на 25, а 25 на 75. Возможны два варианта. Пусть произведение х×у оканчивается на 25. Тогда среди остальных множителей надо выбрать множитель вида 4n+1. Если таких множителей нет, то все 23 оставшихся множителя имеют вид 4n+3. Но в этом случае произведение всех чисел будет оканчиваться на 75. Аналогично рассматривается случай, когда произведение х×у оканчивается на 75.
7. Нельзя. Если бы можно было разрезать звезду на 3 выпуклых части, то две из них содержали бы по две вершины этой звезды. Вместе с вершинами они должны содержать отрезки, соединяющие эти вершины. Но такие отрезки обязательно пересекутся.
10 класс.
1. Заметив, что последняя цифра произведения двух чисел зависит только от последних цифр сомножителей, проследим, как меняется последняя цифра при возведении 2003 в степень: 20031 = …3, 20032 = …9, 20033 = …7, 20034 = …1, 20035 = …3 и т.д. Каждая четвертая цифра в этой последовательности – единица. Таким образом, 20032004 оканчивается на 1. Аналогично получаем последовательность последних цифр при возведении в степень числа 2004: 4, 6, 4, 6, … Последняя цифра числа 20042003 равна 4. Тогда последняя цифра суммы равна 5.
2. 
При х = 0 функция не определена. Если х > 0, то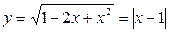 
. Если x < 0, то 
, то есть при отрицательных значениях х функция не определена. График этой функции изображен на чертеже.
3. Заметим, что 99! = (1×99)×(2×98)×(3×97)×…×(49×51)×50. Каждое из записанных в скобках произведений имеет вид (50+n)(50–n) = 502–n2, что меньше 502. Отсюда следует, что 99! < 5099.
4. Пусть площади этих треугольников равны х, х+1, х+2 и х+3. Тогда площадь четырехугольника равна 4х+6. Заметим, что площадь треугольника BCD в 4 раза больше площади треугольника ЕСК, а потому она может равняться либо 4х, либо 4х+4. Но тогда площадь треугольника ABD равняется либо (4х+6)-4х = 6, либо (4х+6)-(4х+4) = 2.
5. Предположим, что n2 = 1111…11. Очевидно, что n должно быть нечетным числом, n = 2k+1, n2 = 4k2+4k+1, то есть при делении на 4 это число дает в остатке 1. С другой стороны, 111…11 при делении на 4 дает в остатке 3, что опровергает наше предположение.
6. Пусть А и В – две наиболее удаленные друг от друга точки. Тогда единичные круги с центрами в точках А и В содержат все остальные точки. Действительно, пусть С – какая-то из 997 оставшихся точек. Среди точек А, В и С найдутся две, расстояние между которыми не превышает 1. Так как АС £ АВ и ВС £ АВ, то одно из расстояний АС или ВС не превышает 1. То есть точка С попадает в один из кругов.
7. Пусть a, b c и d – данные числа, s – их сумма. Будем считать, что s делится на а, b и с, причем а < b < c. Так как числа начинаются с одной цифры, то отношение самого большого из них к самому маленькому меньше 2. В частности 0,5c<d<2c; 0,5c<b<c; 0,5c<a<c. Отсюда 2,5c < s < 5c. Рассуждая аналогично, получим: 0,5b<d<2b; b<c<2b; 0,5b<a<b, откуда 3b<s<6b. Так же имеем 3,5a<s<7a. Учитывая, что s делится на a, b и с нацело, получим: 
Так как а < b < c, то возможны четыре варианта: 1) s=3c=4b=5a; 2) s=4c=5b=6a; 3) s=3c=5b=6a; 4) s=3c=4b=6a. Третий и четвертый вариант невозможны, так как невозможно равенство с=2а. В первом варианте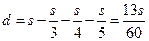 
, во втором варианте 
, что невозможно, так как получается d>2a. То есть искомые числа равны 
. Чтобы эти числа были целыми, необходимо чтобы s делилось на 60, т.е. s=60k, и числа равны 20k, 15k, 12k и 13k. Разница между наибольшим и наименьшим числами не превосходит 100, поэтому k<13. Сдругой стороны 12k³100, то есть k>8. Подбором находим k=9 и тем самым числа равны 180, 135, 108 и 117.
11 класс
1. Так как cos1 < 1, косинус в первой четверти убывает, то cos(cos1)>cos1.
2. Рассмотрим многочлен p(x) = ах2+bx+c. Из условия следует, что этот многочлен не имеет корней. Кроме того, р(1) = a+b+c > 0. То есть все значения р(х) положительны, а потому a>0 (ветви параболы направлены вверх) и с = р(0) >0.
3. После небольших преобразований уравнение примет вид: ху – 10х + 10у –100 = –271 или (х+10)(у–10) = –271. Число 271 является простым, поэтому возможны 4 случая: 1) х+10=–1, у–10=271; 2) х+10=1, у–10=–271; 3) х+10=–271, у–10=1; 4) х+10=271, у–10=–1. Откуда имеем 4 целочисленных решения данного уравнения: (–11; 281); (–9;–261); (261; 11); (261; 9).
4. Из второго уравнения следует, что ху ³ 1, а 4ху ³ 4. Из первого уравнения имеем (х+у)2=4. Вычитая это равенство из неравенства 4ху ³ 4, получим –(х–у)2 ³ 0, что возможно лишь при х=у. Отсюда нетрудно получить решение системы: х=у=1; z=0.
5. Введем систему координат так, чтобы ось ОХ содержало основание треугольника, а ось ОУ его высоту. Вершины треугольника будут иметь следующие координаты: А(–а; 0), С(а; 0), В(0; b). Центр окружности О и точка пересечения высот К будут иметь соответственно координаты (0; r) и (0; 2r). Условие перпендикулярности векторов 
запишется с помощью скалярного произведения как а2 = 2rb. Равенство углов АСО и ВСО запишется следующим образом: r2b+2ra2 = ba2. Из этих двух равенств получим r = 2,5b. Отсюда нетрудно получить, что cosA =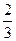 
, т.е. ÐА = ÐС = arccos 
; ÐB = 
.
6. Проекция правильного тетраэдра на плоскость может быть либо треугольником, и тогда ее максимальная площадь равна 
(а – ребро тетраэдра), либо четырехугольником, длины диагоналей которого не превышают а. В этом случае максимальная площадь проекции равна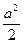 
. Эта площадь получается в том случае, когда диагонали перпендикулярны и имеют длину а, то есть диагонали параллельны плоскости, на которую проектируются. Так как 
, то отсюда следует утверждение задачи.
7. Если число х является корнем данного уравнения, то его корнями являются также числа 1–х и х–1. Один из корней уравнения легко найти подбором: 
. Но тогда легко определить все его корни: 
; 
; 
; 
; 
. Так как данное уравнение является уравнением 6 степени, то других корней оно не имеет.
Дата добавления: 2019-01-14; просмотров: 173; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!