СТРУКТУРНО-ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ 24 страница

M . Попович. Киев, В. Садовский. Москва.

ТЕОРИЯ ГРАФОВ — одна из ветвей топологии. Графом называют геометрии, схему, представляющую собой систему линий, связывающих какие-то заданные точки. Точки наз. вершинами, а связывающие их линии — ребрами (или дугами). Все задачи Т. г. могут решаться как в графической, так и в матричной форме. В случае записи в матричной форме возможность передачи сообщения из данной вершины в другую обозначается единицей, а ее отсутствие — Щ'лем.

Зарождение Т. г. в 18 в. связано с математич. головоломками, но особенно сильный толчок ее развитию был дан в 19 в. и гл. обр. в 20 в., когда обнаружились возможности ее практич приложений: для расчета радиоэлектронных схем, решения т. и. транспортных задач и др. С 50-х гг. Т. г. все шире используется в социальной психологии и социологии.

В области Т. г. следует назвать работы Ф. Харари, Дж. Кемени, К. Фламента, Дж. Снелла, Дж. Френча, Р. Нормана, О. Оэзера, А. Бейвеласа, Р. Вейса и др. В СССР по Т. г. работают Ф. М. Бородкин и др.

Язык Т. г. хорошо приспособлен для анализа разного рода структур и передачи состояний. В соответствии с этим можно выделить след. типы социологич. и социально-психологич. задач, решаемых с помощью Т. г.

1) Формализация и построение общей структурной модели социального объекта на разных уровнях его сложности. Напр., структурная схема организации, социограммы, сравнение систем родства в разных обществах, анализ ролевой структуры групп и т. д. Можно считать, что ролевая структура включает три компонента: лица, позиции (в упрощенном варианте — должности) и задачи, выполняемые в данной позиции. Каждая компонента может быть представлена в виде графа*

208

ТЕОРИЯ ГРАФОВ—ТЕОРИЯ ИГР

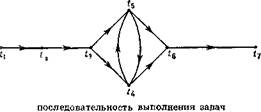
Можно совместить все три графа для всех позиций либо только для одной, и в результате мы получаем ясное представление о конкретной структуре к.-л. данной роли. Так, для роли позиции Р_ь имеем граф (рис.). Вплетение неформальных отношений в указанную формальную структуру значительно усложнит граф, но зато он будет более точной копией действительности.

2) Анализ получен
ной модели, выделение
в ней структурных еди
ниц (подсистем) и изу
чение их связей. Таким
способом могут быть вы
делены, напр., подсистемы в крупных орг-циях.

3) Изучение уровней структуры иерархич. орг-ций:
количество уровней, количество связей, идущих из
одного уровня в другой и от одного лица к другому.
На основании этого решаются задачи:

а) количеств, оценки веса (статуса) индивида в иерархич. орг-ции. Одним из возможных вариантов определения статуса является формула:

где г (р) — статус нек-рого лицар,к — величина уровня субординации, определяемая как наименьшее количество шагов от данного лица к своему подчиненному, n_k — количество лиц на данном уровне к. Напр., в орг-ции, представленной след. графом:

вес а = 1-2+2-7+3-4=28; 6=1-3+2-3=9 и, т. д. См. формулу (1)

б) определение лидера группы. Лидер характеризуется обычно большей по сравнению с другими связанностью с остальными членами группы. Как и в предыдущей задаче, здесь также могут быть использованы различные способы для выделения лидера.

Наиболее простой способ дается формулой: г= *^у ,

т. е. частное от деления суммы всех дистанций каждого до всех других на сумму дистанций данного индивида до всех других.

4) Анализ эффективности деятельности данной системы, куда входят также такие задачи, как поиски оптимальной структуры орг-ции, повышение сплоченности группы, анализ социальной системы с т. зр.

ее устойчивости; исследование потоков информации (передачи сообщений при решении задач, влияние членов группы друг на друга в процессе сплачивания группы); при помощи Т. г. решают проблему нахождения оптимальной коммуникационной сети.

В применении к Т. г., так же как к любому матема-тич. аппарату, верно утверждение, что осн. принципы решения задачи задаются содержат, теорией (в данном случае социологией).

Лит.: Б е р ж К., Т. г. и ее применение, пер. с франц.,
М., 1962; К е и е н и Д ж., Снелл Д ж., ТомпсонД т.,
Введение в конечную математику, пер. с англ., 2 изд., М.,1963;
Оре О., Графы я их применение, пер. с англ., М., 1965;
Белых О. В., Беляев Э. В., Возможности примене
ния Т. г. в социологии, в сб.: Человек и общество, вып. 1,
[Л.], 1966; Количеств, методы в социологич. исследованиях,
М., 1966; Беляев Э. В., Проблемы социологич. измере
ния, «ВФ», 1967, № 7; Bavelas. Communication patterns in
task oriented groups, в кн.: Lerner D., Lasswell H,
Policy sciences, Stanford, 1951; К e m e n у J. G., Sne!l J.,
Mathematical models in the social sciences, N.Y., 1962; F 1 a-
m e n t C, Applications ot graph theory to group structure,
N.Y., 1963; Oeser О. А., Нага г у Р., Role structures
and description in terms of graph theory, в кн.: В i d d 1 e
В., Thomas E. J.. Role theory: concepts and research,
N. Y., 1966. Э . Беляев . Ленинград.

ТЕОРИЯ ИГР — теория матем. моделей принятия решений в условиях неопределенности, когда принимающий решение субъект («и г р о к») располагает информацией лишь о множестве возможных ситуаций, в одной из к-рых он в действительности находится, о множестве решений («стратег и й»), к-рые он может принять, и о количеств, мере того «выигрыша», к-рый он мог бы получить, выбрав в данной ситуации данную стратегию. Т. и. является естеств. развитием теорий решения экстремальных задач в условиях вероятностной, статистич. неопределенности (когда принимающий решения субъект информирован дополнительно об априорных вероятностях каждой из возможных ситуаций). В частности, в рамках Т. и. естественно рассматривать модели конфликт о в (т. е. явлений, в к-рых участвуют различные стороны, наделенные различными интересами и возможностями выбирать свои стратегии в соответствии с этими интересами). Т.о., моделями Т. и. можно в принципе описывать содержательно весьма разнообразные явления: вопросы спортивных состязаний и экономич. борьбы, военные, правовые и классовые конфликты, борьбу человека с природой, биологич. борьбу за существование и т. д. Все такие модели принято в Т. и. наз. играми. Существенно, что Т. и. моделирует не только антагонистич. конфликты, но и более сложные взаимоотношения сторон — носителей различных интересов. Следует при этом отличать теоретико-игровое понятие антагонизма от философской категории антагонизма. В Т. и. антагонизм понимается более прямолинейно и исчерпывается равенством по величине и противоположностью по знаку выигрышей игроков-антагонистов.

Важная роль понятия информации (см. Теория информации) в Т. и. предопределяет ее тесную связь с кибернетикой, на основании чего Т. и. квалифицируют иногда как раздел кибернетики. Однако в теоре-тич. отношении Т. и. следует скорее считать отраслью математики, а в практическом — определ. уровнем операций исследования.

Матем. описание игры сводится к перечислению всех участвующих в ней игроков, указанию для каждого игрока множества всех его стратегий, а также ч и с-ленного выигрыша, к-рый он получит после того, как все игроки выберут свои стратегии. В результате игра становится формальным объев-т о м, к-рый поддается матем. анализу. При совр. состоянии Т. и. осн. целями этого анализа являются: 1) выработка критериев целесообразности («оптимальности») поведения игроков в тех или иных классах игр, 2) доказательство существования у игроков в та-

ТЕОРИЯ ИГР 209

ких играх оптимальных стратегий, 3) установление важнейших свойств оптимальных стратегий (и в том числе, если это возможно, формул и алгоритмов для их фактич. вычисления). (Нахождение оптимальных стратегий игроков требует использования сложного тех-нич. аппарата совр. математики, а численное их определение обычно осуществляется с помощью быстродействующей электронной техники.)

Для весьма широкого класса игр целесообразным поведением игроков естественно считать их стремление к ситуациям равновесия, т.е. к таким одновременным выборам игроками своих стратегий, что ни для одного из игроков не будет выгодным отклонение от этой ситуации (т. е. односторонняя замена выбранной стратегии иной). Именно ситуации равновесия могут быть предметом договорных отношений между игроками. Поэтому стремление игроков к ситуации равновесия принято называть принципом осуществимости цели. В случае антагонистич. игр принцип осуществимости цели превращается в принцип м а к с и м и и а (стремление максимизировать минимальный выигрыш, т. е. стремление действовать наилучшим образом в наихудших условиях).

Весьма часто игры не имеют ситуаций равновесия, сконструированных из первоначально заданных стратегий игроков. Это, с одной стороны, означает, что в таких играх игроки лишены возможности действовать целесообразно, а с другой — побуждает искать для игроков естеств. дополнительных возможностей поведения. Так, напр., можно вместо достоверного выбора к.-л. стратегии осуществить случайный выбор стратегии (по жребию или даже прибегая к тому или иному из суеверий, находящих тем самым практич. применение, хотя и довольно скромное), к-рый наз. с м е-гп а н н о й стратегией. Оказывается, что в большинстве практически важных случаев из смешанных стратегий удается строить ситуации равновесия. Описанный факт является (открытым в Т. и.!) примером целесообразности введения случайного в процесс принятия решений по воле принимающего решения субъекта. Наоборот, применение смешанных стратегий и др. игроками заставляет предполагать, что принятие решения происходит в случайных условиях с заданными априорными вероятностями. Тем самым, однако, эти вероятности приобретают уже не априорное, а оптимизационное происхождение.

Игры можно классифицировать по различным признакам.

Во-первых, следует выделить коалиционные игры, в к-рых принимающие решения игроки согласно правилам игры объединены в фиксиров. коалиции двух типов: коалиции действий и коалиции интересов. Члены одной коалиции действий могут свободно обмениваться информацией и тем самым принимать полностью согласованные решения. Члены одной коалиции интересов имеют единые интересы, и выигрыши коалиции разделению между игроками не подлежат. Существенным является то, что один и тот же игрок может одновременно быть участником неск. коалиций. Коалиционным играм противостоят бескоалиционные игры, в к-рых каждая коалиция состоит лишь из одного игрока. Т. н. кооперативная теория бескоалиционных игр допускает временные объединения игроков в коалиции в процессе игры с последующим разделением полученного общего выигрыша.

Во-вторых, играм в нормальной форме, в к-рых игроки получают всю предназначенную для них информацию до начала игры, противостоят динамические игры, где информация поступает к игрокам постепенно отд. порциями или даже непрерывным во времени потоком. В соответствии с

этим принятие решений участником игры в нормальной форме является однократным актом, тогда как в динамич. игре принятие решения развертывается в дискретный или непрерывный процесс принятия частичных решений. Ввиду ограниченности памяти игрока (т. е. способности хранить п использовать в процессе игры информацию об обстановке и о собственных прошлых действиях) в динамич. играх рассматриваются также случаи полной или частичной утраты информации. Особенности памяти игрока позволяют в ряде случаев упрощать поиски его оптимальных стратегий. Так как в каналах, подводящих к игрокам информацию, могут быть помехи, а пропускные способности этих каналов ограничены, игрок может в ходе игры получать информацию с искажениями и с запаздыванием. Эти обстоятельства также могут находить отражение в формулировках игр.

В-третьих, для матем. анализа игр существенно количество стратегий игроков. Если каждый игрок имеет конечное число стратегий, то игра наз. конечной, а в противном случае — бесконечной. Переход от конечных к бесконечным играм сопровождается качеств, изменением свойств игры и, в частности, оптимальных стратегий ее участников и требует привлечения существенно более сложного матем. аппарата.

Нахождение оптимальных стратегий игроков в конечных антагонистич. играх в нормальной форме (такие игры обычно наз. матричными) эквивалентно решению общей задачи линейного программирования— важной модели мн. экономич. явлений, как и вообще различных явлений организации. При «экономическом» подходе стратегии одного игрока можно интерпретировать как ассортименты выпускаемой продукции, а стратегии другого — как нормированные цены на отд. виды продукции. Оптимальная стратегия игрока будет состоять при этом в выпуске такого ассортимента продукции, что при любых нормированных ценах его гарантированный доход будет максимальным.

Теоретико-пгровые модели требуют особенно пристального рассмотрения как с философской, так и с идеологич. точек зрения, потому что по большей части они являются матем. моделями конфликтов. Конфликты же (в теоретико-игровом понимании этого слова) возможны лишь между сознат. индивидуумами и коллективами, способными предпринимать целеустремленные действия. Тем самым Т. и. оказывается теорией моделей явлений, происходящих в человеческом обществе и неизбежно имеющих поэтому классовый, политич. характер. Поэтому всякое моделирование любого явления игрой становится науч. творчеством с определенных идеологич. позиций.

Осн. проблема моделирования процессов принятия решений в условиях неопределенности (а также в условиях конфликта) касается качеств, адекватности типа игры как матем. модели, необходимости учета в ней тех пли иных частных черт моделируемого явления. Напр., конфликт двух сторон может на первый взгляд ввиду своей остроты расцениваться как антагонистический (т. е. как подлежащий моделированию антагонистич. игрой), тогда как при внимательном рассмотрении более точной его моделью оказывается нек-рая более сложная игра. Др. проблема связана с правильностью количеств, оценок параметров игры — значений выигрышей игроков в тех или иных ситуациях. Трудность такого определения усугубляется тем, что выигрыш игрока может оказаться не только детерминированной, но и случайной величиной. Последнее имеет, напр., место в условиях использования игроками смешанных стратегий.

Практич. применение Т. и. ввиду трудностей построения достаточно адекватных моделей пока ограниченно. Самыми разработанными являются теоретико-

210

ТЕОРИЯ ИНФОРМАЦИИ

игровые модели, описывающие наиболее четкие конфликты военного содержания. Вместе с тем довольно часто количеств, выводы, полученные на основе анализа моделей Т. и., можно рассматривать как качественные соображения при принятии решений в реальных условиях. Даваемый Т. и. анализ принятия решений в условиях неопределенности можно использовать для прогнозирования последствий от принятия этих решений. В частности, методы Т. и. позволяют в принципе оценивать и исходы достаточно простых по содержанию (но не по объему или уровню) и обозримых военных конфликтов (дуэли с небольшим числом выстрелов, схемы поиска, распределение сил п т. д.). Точность такой оценки зависит от степени адекватности игры как модели.

Первой науч. работой, к-рую можно отнести к совр. Т. и., является статья Э. Цермело (1913) о применении теории множеств к шахматной игре. В 20-х гг. были опубликованы результаты Э. Бореля, Кальмара и Дж. Неймана, содержащие ряд важных идей Т. и. Возникновение Т. и. как целостной матем. дисциплины связано с появлением основополагающей монографии Неймана и Моргенштерна («Theory of games and economic behavior», Princeton, 1944). В наст, время по Т. и., и в т. ч. по методологпч. вопросам Т. и., публикуется большое количество книг и статей. Во многих советских и зарубежных ун-тах читаются курсы лекций по Т. и. В 1968 была проведена 1-я Всесоюзная конференция по Т. и. (г. Ереван).

Лит:: Лью с Р. Д. и Райфа X., Игры и решения,
пер. с англ., М., 1961; Матричные игры. Сб. переволов, М.,
1961; Бесконечные антагонистические игры, М., 1963; Кар
лик С, Математические методы в теории игр, программиро-
ваниий экономике, пер. с англ., М., 1964; Воробьев Н. Н.,
Некоторые методологические проблемы теории игр, «ВФ»,
1966, №1. Н. Воробьев. Ленинград.

ТЕОРИЯ ИНФОРМАЦИИ — теория, изучающая законы и способы измерения, преобразования, передачи, использования и хранения информации. В Т. и. и ее технич. приложениях центральными являются понятия количества информации и его меры. Эти понятия в известной степени'соответствуют интуитивным представлениям о количеств, оценке информации, к-рая естественно связывается с числом возможных вариантов сообщения и со степенью его неожиданности. Т. и. возникла как результат осмысления процессов шередачи сообщений, вызванного запросами практики: развитие технич. средств электросвязи требовало количественных критериев для сравнения разнородных способов передачи (телеграф, телефон, телевидение). В 1928 амер. специалист по связи Р. Хартли предложил меру информации, к^рая не зависела от способов передачи и формы сигналов в передающих каналах, а также от содержания и психологич. аспектов передаваемых сообщений. Он воспользовался универсальным свойством процессов связи: каждое сообщение — независимо- от его природы, содержания и назначения — выбирается отправителем из заранее известного получателю множества возможных различных сообщений; поэтому на приемном конце важно знать только результат (случайного для получателя) выбора, а неопределенность результата до выбора сообщения при прочих равных условиях зависит от общего числа возможных сообщений — т. Т. о., количество информации может быть измерено мерой неопределенности выбора, к-рая уничтожается после выбора сообщения. Хартли предложил логарифмич. меру неопределенности выбора: Н = к -log_am (к — коэффициент пропорциональности), к-рая обладает полезным свойством аддитивности и сводит процесс измерения информации к линейному сравнению с единицей меры, т. к. для двух различных множеств сообщенпй1од_а (т₁ ■ т₂) = = log_am₁-J-log_am₂=.ff₁-f Н_г. Выбор основания логариф-

ма а обусловливается областью применения меры информации; и т. к. с развитием вычислит, техники и новых средств связи распространение получила двоичная система счисления, то часто принимают £=1, а = 2. Наиболее простой выбор — выбор между двумя равными возможностями, дает одну двоичную единицу информации, пли бит (сокр. от англ. binary digit);, при то=2, log₂ 2=1.

Дата добавления: 2019-01-14; просмотров: 182; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 58 59 60 61 626364 65 66 67 Следующая ⇒

Мы поможем в написании ваших работ!