Классы ФАЛ. Теорема Поста – Яблонского
Определим предварительно пять классов булевых функций. Классом К0 булевых функций  сохраняющих константу 0, называется множество функций вида
сохраняющих константу 0, называется множество функций вида

При фиксированном n число функций этого класса составляет половину всех функций алгебры логики  Классом K1 булевых функций
Классом K1 булевых функций  сохраняющих константу I, называется множество функций вида
сохраняющих константу I, называется множество функций вида  Проверим на принадлежность к классу К0 и К1 функцию
Проверим на принадлежность к классу К0 и К1 функцию





Классом Кл линейных булевых функций 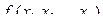 называется множество функций вида
называется множество функций вида
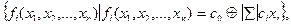


где 
 – знаки операций сложения по модулю два. Число членов этого класса равно 2n+1. Проверим, является ли булева функция
– знаки операций сложения по модулю два. Число членов этого класса равно 2n+1. Проверим, является ли булева функция  линейной. Найдем неизвестные коэффициенты из предположения о линейности этой функции.
линейной. Найдем неизвестные коэффициенты из предположения о линейности этой функции.
На наборе < 0000 >


Аналогично определим коэффициенты С1, С2, С3, С4:



Проверив функцию на наборах (0100), (0010), (0001), получим, что С2 = 0, С3 = 0, С4 = 1. Окончательно получаем

Это равенство в каждой из остальных I I точек не сохраняется. Действительно, в точке (1,1,1,1) имеем
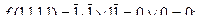


Следовательно, сделанное предложение является неверным. Функция  нелинейная:
нелинейная: 
Классом Кс самодвойственных булевых функций 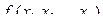 называется множество булевых функций вида
называется множество булевых функций вида

Нетрудно показать, что рассматриваемая в качестве примера функция  не является самодвойственной. Для этого необходимо проверить на всех 2n наборов значение функций
не является самодвойственной. Для этого необходимо проверить на всех 2n наборов значение функций  и
и 
Классом Км монотонных булевых функций  называется множество булевых функций вида
называется множество булевых функций вида
|
|
|

Для определения монотонности необходимо сравнить на всех наборах функцию  И если найдется хотя бы одна пара наборов
И если найдется хотя бы одна пара наборов  таких, что
таких, что 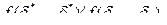 то такая функция немонотонна.
то такая функция немонотонна.
Рассмотренные классы функций определяют возможность выбрать критерий полноты и в дальнейшем минимальный набор функций, достаточный для представления любой. Критерий полноты задается теоремой Поста-Яблонского, которая в наиболее простой формулировке будет следующей:
система S функций алгебры логики  является полной, тогда и только тогда, когда выполняется пять условий: существуют функций
является полной, тогда и только тогда, когда выполняется пять условий: существуют функций  не сохраняющая константу нуль:
не сохраняющая константу нуль:  функция
функция  не сохраняющая константу единица:
не сохраняющая константу единица:  нелинейная функция, несамодвойственная функция и немонотонная функция, в системе S. Выбрав, как ранее из табл. 4.4, функции
нелинейная функция, несамодвойственная функция и немонотонная функция, в системе S. Выбрав, как ранее из табл. 4.4, функции  (основные функции алгебры логики), построим таблицу и найдем все базисы.
(основные функции алгебры логики), построим таблицу и найдем все базисы.
Преобразуем мультипликативно-аддитивную форму в аддитивно-мультипликативную; порождаем все покрытия столбцов строками таблицы 4.13






Каждое из полученных покрытий  порождает базис
порождает базис 
 базис Вебба;
базис Вебба;
 базис Шеффера;
базис Шеффера;

 импликативный базис;
импликативный базис;


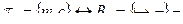 коимпликативный базис;
коимпликативный базис;
 импликативный базис;
импликативный базис;
 конъюнктивный базис;
конъюнктивный базис;
|
|
|
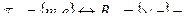 дизъюнктивный базис;
дизъюнктивный базис;
 коимпликативный базис;
коимпликативный базис;




 базис Жегалкина;
базис Жегалкина;

Техническая реализация базисных функций может быть основана на использовании различных физических явлений. Согласно ГОСТ 2.743-72.
Таблица 4.13
| Идентификатор строки | Функция | Классы | ||||
| К0 | К1 | Кл | Кс | Км | ||

| 0 | 1 | 1 | |||
| b | 1 | 1 | 1 | |||
| c | 2 | 1 | 1 | 1 | 1 | |
| d | 6 | 1 | 1 | 1 | ||
| e | 7 | 1 | 1 | |||
| g | 8 | 1 | 1 | 1 | 1 | 1 |
| k | 9 | 1 | 1 | 1 | ||
| m | 12 | 1 | 1 | 1 | ||
| n | 13 | 1 | 1 | 1 | 1 | |
| p | 14 | 1 | 1 | 1 | 1 | 1 |
| r | 15 | 1 | 1 | |||
базисные элементы графически изображают в виде прямоугольника, в которых инверсные входы и выходы изображают в виде незаштрихованых кружков и ставят 1, если внешняя связка «дизъюнкция», и – &, если – «конъюнкция», за исключением сложения по модулю два (тогда сверху ставят М2) и эквивалентности (обозначают =) (рис. 4.1) [13].

Рис. 4.1
Синтез логических схем
Синтез логических схем можно производить в любом базисе, который обеспечен элементной базой, позволяющей реализовать все функции, входящие в базис. Очевидно, сложность синтезируемой схемы будет определяться сложностью формулы, описывающей конкретную функцию, и заданной в виде таблицы истинности.
|
|
|
Рассмотрим задание функции принятия решения комитетом "трех". Каждый член комитета при одобрении закона нажимает свою кнопку, если большинство членов согласны, то резолюция принимается, что фиксируется регистрирующим прибором. Устройство, которое реализует данную функцию, имеет таблицу истинности (табл.414). От таблицы истинности всегда можно перейти к ФАЛ с помощью алгоритма построения совершенной дизъюнктивной или совершенной конъюнктивной нормальной формы.
Рассмотрим алгоритм нахождения совершенной дизъюнктивной нормальной формы (СДНФ).
1. Отмечаем наборы, на которых функция принимает значение 1.
Для функции (табл.4.14) это наборы 011, 101, 110, 111.
2. Переменные  , принявшие в этих наборах значение 1, обозначаем как
, принявшие в этих наборах значение 1, обозначаем как  , а принявшие значение 0 – как
, а принявшие значение 0 – как  .
.
3. Для каждого набора записываем элементарную конъюнкцию ранга n, состоящую из  и
и  Для отмеченных наборов табл.4.14 это есть
Для отмеченных наборов табл.4.14 это есть 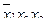



4. Объединяем элементарные конъюнкции ранга n знаком дизъюнкции, в результате получаем совершенную дизъюнктивную нормальную форму. Для рассматриваемого примера 
| х1 | х2 | х3 | 
|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
|
|
|
Аналогично может быть найдена совершенная конъюнктивная нормальная форма. Эту задачу можно рассматривать как двойственную к задаче нахождения СДНФ.
1. Отмечаются наборы функций, на которых она принимает значение
0 (это наборы 000, 001, 010, 100).
2. Переменные х і, принявшие на этих наборах значение I, приравниваем к  , а принявшие 0 – х i;
, а принявшие 0 – х i;
3. Для каждого набора записывается дизъюнкция переменных, соответствующая этому набору. Для нашего примера это

4. Объединяем полученные дизъюнкции знаком конъюнкции, в результате получаем совершенную конъюнктивную нормальную форму. Для
рассматриваемого примера СКНФ  =
= 

Объединяя сказанное, можно считать, что СДНФ – это дизъюнкция конъюнктивных объединений аргументов, соответствующих единичным значениям функции, а СКНФ – это конъюнкция дизъюнктивных объединений, соответствующих нулевым значениям ФАЛ. При этом в первом случае единичному значению аргумента соответствует х і, а во втором – 
Оба алгоритма являются следствиями разложения Шеннона функции алгебры логики. Действительно, если ввести степень аргумента согласно правилу

которое сводится к четырем возможным решениям
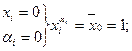



то любая элементарная конъюнкция ранга n может быть записана в виде  Она не обращается в нуль только в том случае, если
Она не обращается в нуль только в том случае, если 
 Тогда справедлива.
Тогда справедлива.
Теорема [13]. Любая функция f(x1,..., хn) представима в виде разложения Шеннона:
 по всем наборам
по всем наборам 

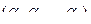 .
.
Подставим произвольно вместо первых k переменных их значения 
 Тогда левая часть доказываемой формулы равна
Тогда левая часть доказываемой формулы равна 
 Правая часть представляет собой дизъюнкцию 2k конъюнкций вида
Правая часть представляет собой дизъюнкцию 2k конъюнкций вида  которые этой подстановкой разобьются на два класса. К первому классу относится конъюнкция, у которой набор
которые этой подстановкой разобьются на два класса. К первому классу относится конъюнкция, у которой набор  совпадает с набором
совпадает с набором 

 …
… 

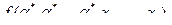
Эта конъюнкция равна левой части формулы. Ко второму классу относятся 2к-1 конъюнкций, у каждой из которых хотя бы в одной переменной  . Следовательно, каждая из них равна нулю. Тогда на основании соотношения
. Следовательно, каждая из них равна нулю. Тогда на основании соотношения  получаем, что левая и правая части формул равны при любой подстановке переменных
получаем, что левая и правая части формул равны при любой подстановке переменных  В предельном случае (k = n) для любой ФАЛ f(x1,...,хn), не равно нулю,
В предельном случае (k = n) для любой ФАЛ f(x1,...,хn), не равно нулю,

по всём наборам  где
где 
т.е. имеем совершенную дизъюнктивную нормальную форму. Аналогично записывается двойственное разложение Шеннона:
 по всем наборам
по всем наборам 
и его предельный случай

по всем наборам  где
где 
является совершенной конъюнктивной нормальной формой функции 
Разложение Шеннона дает возможность представить любую функцию от n переменных через функции от (n – m) переменных, называемых остаточными функциями. Так, например, при m = 1 имеем представление функции от п переменных через функции от (n – 1) переменной (нулевую и единичные остаточные функции первого порядка от аргументу хк):

Разложение Шеннона и алгоритмы получения СДНФ и СКНФ представляют любую функцию алгебры логики в базисе  который может быть приведен к базисам
который может быть приведен к базисам  или
или  с помощью формул до Моргана. Поэтому остановимся более подробно на представлении функций алгебры логики в базисе
с помощью формул до Моргана. Поэтому остановимся более подробно на представлении функций алгебры логики в базисе  . Во-первых, покажем, что представление Функции в СДНФ (или соответственно в СКНФ) неэкономно. Для этого введем определение. Переменную или ее отрицание будем называть первичным термом. Количество первичных термов, которые образуют логическую формулу, называется ее сложностью и обозначается
. Во-первых, покажем, что представление Функции в СДНФ (или соответственно в СКНФ) неэкономно. Для этого введем определение. Переменную или ее отрицание будем называть первичным термом. Количество первичных термов, которые образуют логическую формулу, называется ее сложностью и обозначается  Так, в задаче о голосовании (см. табл. 4. 14) сложность СДНФ найденной функции
Так, в задаче о голосовании (см. табл. 4. 14) сложность СДНФ найденной функции  будет
будет  = 12. Очевидно, что при реализации функций алгебры логики в виде некоторых устройств необходимо найти некоторые представления их, имеющее наиболее экономную реализацию.
= 12. Очевидно, что при реализации функций алгебры логики в виде некоторых устройств необходимо найти некоторые представления их, имеющее наиболее экономную реализацию.
Для нахождения более экономных решений используются, основные законы, справедливые для функций выбранного базиса. В настоящее время наибольшие результаты получены для базиса  , и этот базис обеспечен лучше других наборами функциональных интегральных элементов. Перед решением задачи о нахождении некоторых экономичных форм представления ФАЛ введем ряд понятий и определений.
, и этот базис обеспечен лучше других наборами функциональных интегральных элементов. Перед решением задачи о нахождении некоторых экономичных форм представления ФАЛ введем ряд понятий и определений.
Конъюнкция,  называется элементарной, если в этой конъюнкции каждое переменное, от которого зависит ФАЛ, встречается не более одного раза.
называется элементарной, если в этой конъюнкции каждое переменное, от которого зависит ФАЛ, встречается не более одного раза.
Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ). Отсюда следует, что СДНФ является самой сложной ДНФ, так как объединяет конъюнкции длиной n (ранга n). Число элементарных конъюнкций, входящих в ДФ, называется ее длиной; ДФ, имеющая наименьшую длину по сравнению со всеми другими ДФ, эквивалентными данной функции, называется кратчайшей ДНФ (КДНФ).
Дизъюнктивная нормальная форма, содержащая наименьшее число букв 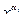 по сравнению со всеми другими (имеющая наименьшую сложность), эквивалентными данной функции, называется минимальной для ДНФ (МДНФ). Аналогичные определения можно дать и для конъюнктивных нормальных форм [16, 17].
по сравнению со всеми другими (имеющая наименьшую сложность), эквивалентными данной функции, называется минимальной для ДНФ (МДНФ). Аналогичные определения можно дать и для конъюнктивных нормальных форм [16, 17].
Еще раз подчеркнем, что мы будем, рассматривать лишь класс аналитических представлений для функций f(x1,..,xn), определяемой общей формулой  где
где  – элементарные конъюнкции различных рангов.
– элементарные конъюнкции различных рангов.
Таким образом, задача нахождения экономного представления сводится частично к задаче нахождения минимальной дизъюнктивной нормальной формы. На основании свойств  , – были получены две операции, поз-воляющие значительно упростить аналитическое представление ФАЛ. Этими операциями являются операция склеивания
, – были получены две операции, поз-воляющие значительно упростить аналитическое представление ФАЛ. Этими операциями являются операция склеивания 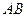

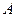
 =
= 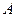 , которая доказывается элементарно
, которая доказывается элементарно 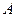 (
(  ) =
) = 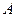 , так как
, так как 
 =
=  , и элементарного поглощения
, и элементарного поглощения  =
= 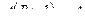 ( аналогично имеются и для конъюнктивного представления операция склеивания
( аналогично имеются и для конъюнктивного представления операция склеивания 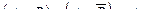 и поглощения
и поглощения  ).
).
Если их применять к СДНФ (или любой исходной ДНФ) или СКНФ, то наступит момент, когда они уже будут неприменимы. В этом случае получим тупиковую нормальную форму. Тупиковых форм может быть несколько. Вид каждой зависит от порядка применения операций поглощения и склеивания к элементарным конъюнкциям. Получая все возможные тупиковые формы для конкретной функции и сравнивая их по сложности (количеству  ), можно найти все минимальные формы. Однако оказалось, что число тупиковых ДНФ
), можно найти все минимальные формы. Однако оказалось, что число тупиковых ДНФ  при большом
при большом  довольно велико
довольно велико  :
:
 . (4.11)
. (4.11)
Таким образом, уже для  порядка 10-15 перебор становится весьма большим и процесс нахождения МДНФ становится малоэффективным. Поэтому усилиями специалистов, работавших в 60-х гг., были созданы методы нахождения МДНФ, ориентированные на использование ЭВМ. Вначале опишем наиболее простой по своим идеям метод неопределенных коэффициентов. Рассмотрим его на примере функции от трех переменных. Для этого запишем функцию ƒ
порядка 10-15 перебор становится весьма большим и процесс нахождения МДНФ становится малоэффективным. Поэтому усилиями специалистов, работавших в 60-х гг., были созданы методы нахождения МДНФ, ориентированные на использование ЭВМ. Вначале опишем наиболее простой по своим идеям метод неопределенных коэффициентов. Рассмотрим его на примере функции от трех переменных. Для этого запишем функцию ƒ 
 в виде следующей ДНФ:
в виде следующей ДНФ:





 (4.12)
(4.12)
Здесь представлены все возможные конъюктивные члены, которые могут входить в дизъюнктивную форму представления  Коэффициенты k с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого ДНФ была минимальной. Если теперь задавать всевозможные наборы значений аргументов
Коэффициенты k с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого ДНФ была минимальной. Если теперь задавать всевозможные наборы значений аргументов  и приравнивать получен-ное после этого выражение к значению функции на выбранных наборах, то получим систему 23 уравнений для определения коэффициентов k:
и приравнивать получен-ное после этого выражение к значению функции на выбранных наборах, то получим систему 23 уравнений для определения коэффициентов k:







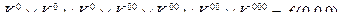
Значение правых частей этой системы уравнений определяет конкретную функцию. Если набор  такой, что на нем функция равна нулю, то в правой части соответствующего уравнения будет стоять нуль. Для удовлетворения этого уравнения необходимо приравнять к нулю все коэффициенты К, входящие в левую часть рассматриваемого уравнения. Рассмотрим все наборы, на которых данная функция обращения в нуль, получим вое нулевые коэффициенты К. В уравнениях, в которых справа стоят единицы, вычеркнем слева все нулевые коэффициенты. Из оставшихся коэффициентов приравняем к единице коэффициент, определяющий конъюнкцию наименьшего возможного ранга, а остальные коэффициенты в левой части данного уравнения примем равными нулю. Взяв по одному коэффициенту из каждой строки и приведя подобные согласно правилу
такой, что на нем функция равна нулю, то в правой части соответствующего уравнения будет стоять нуль. Для удовлетворения этого уравнения необходимо приравнять к нулю все коэффициенты К, входящие в левую часть рассматриваемого уравнения. Рассмотрим все наборы, на которых данная функция обращения в нуль, получим вое нулевые коэффициенты К. В уравнениях, в которых справа стоят единицы, вычеркнем слева все нулевые коэффициенты. Из оставшихся коэффициентов приравняем к единице коэффициент, определяющий конъюнкцию наименьшего возможного ранга, а остальные коэффициенты в левой части данного уравнения примем равными нулю. Взяв по одному коэффициенту из каждой строки и приведя подобные согласно правилу  получим набор коэффициентов, который определяет элементарные конъюнкции, входящие в МДНФ.
получим набор коэффициентов, который определяет элементарные конъюнкции, входящие в МДНФ.
Пусть на основе табличной записи ФАЛ согласно алгоритму нахождения СДНФ была получена функция

Запишем для нее систему уравнений:
1) 
2) 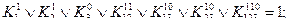
3) 
4) 
5) 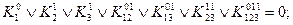
6) 
7) 
8) 
Из уравнений 5, 6 и 7 в силу свойств дизъюнкции получаем 
После исключения этих коэффициентов исходная система примет вид




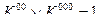
Приравняем к единице каждый крайний слева коэффициент, а остальные – нулю. Получим





Отсюда  и
и  Метод неопределенных коэффициентов (и аналогичный ему метод минимизирующих карт) характеризуется тем, что для минимизируемой функции нужно знать все элементарные конъюнкции, которые могут входить в ДНФ этой функции. При этом число уравнений равно 2n, а число членов в каждом уравнении 2n – 1. Это показывает, что при n > 8 + 9 система уравнений становится громоздкой.
Метод неопределенных коэффициентов (и аналогичный ему метод минимизирующих карт) характеризуется тем, что для минимизируемой функции нужно знать все элементарные конъюнкции, которые могут входить в ДНФ этой функции. При этом число уравнений равно 2n, а число членов в каждом уравнении 2n – 1. Это показывает, что при n > 8 + 9 система уравнений становится громоздкой.
Рассмотрим метод, который использует перебор не всех возможных конъюнкций для функции от n переменных, а только тех, которые могут присутствовать в ДНФ, эквивалентной минимизируемой функции. Этот метод был предложен в 1956 г. Мак-Класки, который усовершенствовал метод Квайна в направлении уменьшения перебора. С этой целью исходная функция, заданная в СДНФ, задается в виде двоичных наборов, на которых она равна единице. Двоичные наборы группируются в подгруппы по числу единиц в двоичном наборе. Двоичные наборы, соответствующие элементарным конъюнкциям ранга n и различающиеся на одну единицу, проверяются на склеивание. В результате получаются элементарные конъюнкции ранга n–1. Все элементарные конъюнкции ранга n, для которых невозможна операция склеивания, выписываются отдельно и называются первичными импликантами ранга n. Они должны обязательно входить в так называемую первичную импликантнуго таблицу. Полученные элементарные конъюнкции ранга n–1 также разбиваются на группы по числу единиц, и происходит сравнение между элементарными конъюнкциями соседних групп на склеивание. Элементарные конъюнкции ранга n–1, которые не могут быть склеены, дописываются в список первичных импликант, а полученные элементарные конъюнкции ранга n–2 снова разбиваются по группам, и процесс продолжается до тех пор, пока возможна хотя бы одна операция склеивания. После того как операция склеивания становится неприменимой, все оставшиеся элементарные конъюнкции ранга n – m дописываются в число первичных импликант, и находится минимальное покрытие набором первичных импликант исходной функция; минимальный покрывающий набор и будет составлять МДНФ. Рассмотрим действие этого алгоритма на примере. Пусть задана СДНФ функции  на наборах с номерами 3, 4, 5, 7, 9, 11, 12, 13. Выпишем двоичные эквиваленты номеров (наборы
на наборах с номерами 3, 4, 5, 7, 9, 11, 12, 13. Выпишем двоичные эквиваленты номеров (наборы  на которых функция принимает значение I): 0011, 0100, 0101, 0111, 1001, 1011, 1100, 1101. Это соответствует функции
на которых функция принимает значение I): 0011, 0100, 0101, 0111, 1001, 1011, 1100, 1101. Это соответствует функции


Напишем двоичные эквиваленты по группам:
нулевая группа: нет;
первая группа: 0100;
вторая группа: 0011, 0101, 1001, 1100;
третья группа: 0111, 1011, 1101.
Сравнивая соседние группы на склеивание, вместо склеенных (исключенных переменных) записываем знак тире. Дня примера, сравнивая 0100 и 0101,получаем 010 – (что соответствует

В результате сравнения и склеивания между двоичными эквивалентами элементарных конъюнкций 4-го ранга были получены элементарные конъюнкции 3-го ранга.
Первая группа: 010- , -100;
вторая группа: 0-11, -011, 01-1, 10-1, 1-01, 110-.
Сравнивая элементарные конъюнкции 3-го ранга, находим элементарные конъюнкции 2-го ранга. Здесь есть только одна – первой группы: это -10-. Элементарные конъюнкции 3-го ранга, которые не склеились, включим в число первичных импликант: 0-11, -01l, 01-1, 10-1, 1-01. Составим таблицу меток, число столбцов которой равно числу наборов, на которых функция принимает значение единица; число строк равно числу первичных импликант (табл. 4.15).
Для нахождения минимального набора импликант, покрывающих всю таблицу (имеющих метки во всех столбцах) и составляющих минимальную дизъюнктивную форму, проделаем следующие операции [I6].
1. Найдем столбцы, в которых одна метка, и выпишем первичные
(существенные) импликанты, дающие эту метку. Для рассматриваемого
примера такой импликантой является -10-. Она должна обязательно содержаться в МДНФ. Исключаем строки, содержащие существенные импликанты и столбцы, имеющие метки, от существенных импликант. Получаем сокращенную импликантиую таблицу (табл. 4.16).
2. Исследуется полученная после первого этапа таблица на наличие столбцов, имеющих абсолютно одинаковые метки. Если такие имеются, то остается только один столбец, остальные вычеркиваются. И снова строится таблица (для данного примера таких столбцов нет).
3. Если после выбрасывания некоторых столбцов на втором этапе
в таблице появляются отроки, в которых нет ни одной метки, то первичные импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения.
4. Выбирается минимальный набор первичных импликант, имеющий метки во всех столбцах. При нескольких возможных вариантах, такого выбора отдается предпочтение варианту покрытия с минимальным суммарным числом букв в простых импликантах, образующих покрытия.
Таблица 4.15
| Первичные импликанты | 0100 | 0011 | 0101 | 1001 | 1100 | 0111 | 1011 | 1101 |
| 0-11 | V | V | ||||||
| -011 | V | V | ||||||
| 01-1 | V | V | ||||||
| 10-1 | V | V | ||||||
| 1-01 | V | V | ||||||
| -10- | V | V | V | V |
Таблица 4.16
| Первичные импликанты | 0011 | 1001 | 0111 | 1011 |
| 0-11 | V | V | ||
| -011 | V | V | ||
| 01-1 | V | |||
| 10-1 | V | V | ||
| 1-01 | V |
Для рассматриваемой функции выбираем 0-11и 10-1. Полученный набор с выбранной ранее первичной существенной импликантой -10- составляют минимальную дизъюнктивную форму функции  Дальнейшее упрощение аналитической записи ФАЛ осуществляется за счет вынесения за скобки. Так, полученную минимальную форму функции
Дальнейшее упрощение аналитической записи ФАЛ осуществляется за счет вынесения за скобки. Так, полученную минимальную форму функции 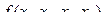 можно записать в виде
можно записать в виде
 уменьшив сложность на единицу.
уменьшив сложность на единицу.
Проблему минимизации можно решить и в других базисах. Основная трудность при этом состоит в построении подходящих характеристических функций в том или ином базисе. Проблема минимизации имеет большое практическое значение, так как она является первым этапом синтеза надежных схем. При практическом использовании методов минимизации надо помнить о принятых допущениях. Во-первых, при подсчете длины аналитического представления не учитывали отрицания над буквами. Если для реализации отрицания в схеме требуется специальный элемент, то, очевидно, при выборе минимальной формы, из множества эквивалентных минимальных форм необходимо выбирать те формы, которые содержат минимальное число отрицаний.
Рассмотрим синтез логических схем. Порядок синтеза зададим следующей последовательностью.
1. По минимальной форме заданной функции находим оптимальную в смысле количества связок V, &, – скобочную форму.
2. Выражаем связки V, &, – в виде суперпозиции заданного базиса (если синтез не в базисе V, &, –).
3. Подставляем результаты п.2 в выражение, полученное в п.1,
отмечая при этом стыки блоков, моделирующие V, &, – в заданном базисе.
4. Анализируем стыки, устраняем избыточность логической схемы,
используя закон двойного отрицания.
Этот метод можно успешно применять при проектировании простых схем. Проектирование сложных логических схем требует применения САПР (систем автоматического проектирования). Один из методов, основанный на разложении Шеннона, дает хорошие результаты. Как известно,


позволяет при наличии блоков исключения k переменных свести реализацию булевой функции от п переменных к реализации функции от 
 переменных. В частности, при k = 1 имеем
переменных. В частности, при k = 1 имеем 

Размерность остаточных функции  в свою очередь можно понизить, исключая t переменных и т. д. до тех пор, пока остаточные функции не будут иметь простой вид и их реализация в заданном базисе не представит затруднений. Сложность остаточных функций зависит от порядка исключения переменных в заданной булевой функции
в свою очередь можно понизить, исключая t переменных и т. д. до тех пор, пока остаточные функции не будут иметь простой вид и их реализация в заданном базисе не представит затруднений. Сложность остаточных функций зависит от порядка исключения переменных в заданной булевой функции  Число возможных способов исключения' переменных растет комбинаторно. Например, при использовании только блоков, исключающих одну переменную на каждом уровне, это число равно n! Но на каждом уровне можно исключать различное число переменных. Выбрать оптимальное решение довольно трудно. В настоящее время имеется один эвристический способ, который основан на анализе множества взаимосвязей переменных, задаваемых ФАЛ. Этот способ основан на понятии производной от функции алгебры логики.
Число возможных способов исключения' переменных растет комбинаторно. Например, при использовании только блоков, исключающих одну переменную на каждом уровне, это число равно n! Но на каждом уровне можно исключать различное число переменных. Выбрать оптимальное решение довольно трудно. В настоящее время имеется один эвристический способ, который основан на анализе множества взаимосвязей переменных, задаваемых ФАЛ. Этот способ основан на понятии производной от функции алгебры логики.
Производная первого порядка  от ФАЛ по переменной х i равна сумме по модулю два остаточных (нулевой и единичной) функций исходной функции алгебры логики
от ФАЛ по переменной х i равна сумме по модулю два остаточных (нулевой и единичной) функций исходной функции алгебры логики 
 (4.13)
(4.13)
Как правило, перед взятием производной находится ее МДНФ. Например

 Производная первого порядка от ФАЛ определяет условия, при которых эта функция изменяет значение при переключении
Производная первого порядка от ФАЛ определяет условия, при которых эта функция изменяет значение при переключении  (изменении значения
(изменении значения  на противоположное). Эти условия выражаются в том, что производная должна быть равна 1.
на противоположное). Эти условия выражаются в том, что производная должна быть равна 1.
Аналогично вводится понятие смешанной производной k-го порядка [I3]:
 (4.14)
(4.14)
Смешанную производную k-го порядка вычисляют последовательным дифференцированием k раз исходной ФАЛ. Производная k-го порядка находится через смешанные производные по формуле
 (4.15)
(4.15)
и определяет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных 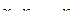 Выражение производной, определяющее это условие, должно быть равно 1. Из анализа наборов переменных, на которых производная принимает значение 1, определяем условия переключения функции
Выражение производной, определяющее это условие, должно быть равно 1. Из анализа наборов переменных, на которых производная принимает значение 1, определяем условия переключения функции  Очевидно, чем больше этих наборов, тем больше условий переключения. Критерий оптимального исключения заключается в исключении сначала переменных, при переключении которых ФАЛ переключается при максимальном числе условий. Это максимальное число определяется весом производной, который определяется числом наборов аргументов ранга n –m (n – число переменных, m – порядок производной), на которых производная принимает значение единица. При использовании блоков исключения m переменных находят производные m-го порядка от реализуемой функции и ищут максимальное значение веса производной:
Очевидно, чем больше этих наборов, тем больше условий переключения. Критерий оптимального исключения заключается в исключении сначала переменных, при переключении которых ФАЛ переключается при максимальном числе условий. Это максимальное число определяется весом производной, который определяется числом наборов аргументов ранга n –m (n – число переменных, m – порядок производной), на которых производная принимает значение единица. При использовании блоков исключения m переменных находят производные m-го порядка от реализуемой функции и ищут максимальное значение веса производной:

которое и определяет исключаемые переменные. Для получения остаточных ФАЛ снова находятся производные определяются веса, а производная от рассматриваемой остаточной функции, имеющая максимальный вес, определяет соответствующие переменные, которые исключаются на этом ярусе для этой остаточной функции и т.д., пока остаточные функции не будут иметь простую реализацию. Рассмотрим простой пример. Пусть была найдена МДНФ ФАЛ от пяти переменных [13]: 
 и имеются в наличии блоки исключения одной переменной (рис. 4.2). Определяем переменную х i, по которой производная
и имеются в наличии блоки исключения одной переменной (рис. 4.2). Определяем переменную х i, по которой производная  имеет наибольший вес, т.е. функция
имеет наибольший вес, т.е. функция  зависит от нее более существительно. Имеем
зависит от нее более существительно. Имеем




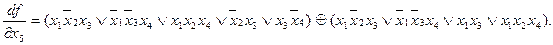
Для нахождения веса  построим таблицу истинности, по которой определяем число наборов, на которых производная принимает единичное значение – это и будет весом
построим таблицу истинности, по которой определяем число наборов, на которых производная принимает единичное значение – это и будет весом  (табл. 4.17).
(табл. 4.17).
Таблица 4.17
| х2 | х3 | х4 | х5 | 
|

| ||||
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Нетрудно видеть, что  принимает единичное значение на семи наборах, т.е.
принимает единичное значение на семи наборах, т.е.  Если построим аналогичные таблицы истинности для
Если построим аналогичные таблицы истинности для  то непосредственным подсчетом числа наборов, на которых производные принимают значение единица, получим
то непосредственным подсчетом числа наборов, на которых производные принимают значение единица, получим





Рис. 4.2
Максимальное значение  получается при дифференцировании функции
получается при дифференцировании функции  по переменной х3. Исключая эту переменную, получаем две остаточные функции – единичную
по переменной х3. Исключая эту переменную, получаем две остаточные функции – единичную  и нулевую
и нулевую 


 Аналогично определяем производные и их веса то единичной и нулевой остаточных функции:
Аналогично определяем производные и их веса то единичной и нулевой остаточных функции:

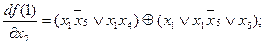
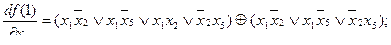

Для нахождения веса строим таблицу истинности, по которой подсчитываем вес (число наборов, на которых  принимает значение единица). Например, для
принимает значение единица). Например, для  построим табл. 4.18 и получим
построим табл. 4.18 и получим

Построив аналогичные таблицы истинности для остальных производных остаточных функций, получим

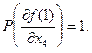

Таблица 4.18
| х2 | х4 | х5 |  (1) (1)
|

| |||
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Максимальное значение производной от единичной остаточной функции получим по переменной х1. Следовательно, она является одной из исключаемых переменных на втором ярусе. Вторую исключаемую переменную определим после дифференцирования нулевой остаточной функции f (0) и нахождения весов  для всех х i:
для всех х i:



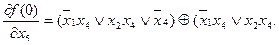
Аналогично, как и для нахождения весов  необходимо построить таблицы истинности для
необходимо построить таблицы истинности для  . Например, для
. Например, для 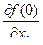 она имеет вид
она имеет вид
Таблица 4.19
| х1 | х2 | х5 |  (1) (1)
|

| |||
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
По табл. 4.19 определяем, что  Аналогично, построив таблицы, можно определить, что
Аналогично, построив таблицы, можно определить, что



В связи с тем, что 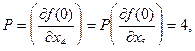 можно выбрать любую переменную для исключения на втором ярусе. Выберем х4; таким образом, на втором ярусе исключаем х1 и х4. Исключая х1, получаем следующее остаточные функции:
можно выбрать любую переменную для исключения на втором ярусе. Выберем х4; таким образом, на втором ярусе исключаем х1 и х4. Исключая х1, получаем следующее остаточные функции:


Исключая х4, получаем остаточные функции следующего вида:


Остаточные функции 


 могут быть реализованы стандартными блоками (см. рис. 4.1). В результате получаем логическую схему, реализующую функцию
могут быть реализованы стандартными блоками (см. рис. 4.1). В результате получаем логическую схему, реализующую функцию  (рис 4.3).
(рис 4.3).

Рис. 4.3
Критерий оптимальности переменных имеет эвристический характер, что основано на предположении о том, что чем больше вес производной  тем больше функция
тем больше функция  зависит от переменной хi. Если имеются блоки исключения m переменных, то построение схемы проводят аналогично, вычисляя вес производных m -го порядка:
зависит от переменной хi. Если имеются блоки исключения m переменных, то построение схемы проводят аналогично, вычисляя вес производных m -го порядка:

Логические исчисления
В современной математике большое распространение получил так называемый аксиоматический метод. Сущность его состоит в своеобразном способе определять математические объекты и отношения между ними. Предположим, что, изучая систему каких-то объектов, мы употребляем определенные термины, выражающие свойства этих объектов и отношения между ними. При этом мы не определяем ни самих объектов, ни этих свойств и отношений, но высказываем ряд определенных утверждений, которые должны для них выполняться. Очевидно, что эти утверждения выделяют из всевозможных систем объектов, их свойств и отношений между ними такие системы, для которых они выполнены. Таким образом, сделанное утверждение можно рассматривать как определение системы объектов определенного класса, их свойств и отношений между ними. Рассмотрим пример.
Пусть дана система каких-то объектов, которые мы будем обозначать буквами латинского алфавита, и между ними установлено отношение, выражаемое термином "предшествует". Не определяя ни объектов, ни отношений "предшествует", мы высказываем для них следующие утверждения:
1) никакой объект не предшествует сам себе;
2) если х предшествует у, а у предшествует z , то х предшествует z .
Нетрудно видеть, что существуют такие системы объектов, с такими отношениями между ними, что если под термином "х – предшествует у" понимать данное отношение, то наши утверждения окажутся истинными. Пусть, например, объектами х, у, ... являются действительные числа, а отношение "х предшествует у" представляет собой "х меньше у"
Здесь утверждения 1 и 2 выполняются.
Системы объектов с одним отношением, для которых положения 1 и 2 выполнимы, образуют определенный класс, а положения 1 и 2 мы можем рассматривать как определение систем этого класса. Утверждения, посредством которых мы таким образом выделяем совокупность объектов, носят название аксиом. Делая логические выводы из аксиом, мы будем получать утверждения, справедливые для любой системы объектов, удовлетворяющих данным аксиомам. Более значительным примером аксиоматического определения является система аксиом геометрии. Соответствие между аксиомами и предметами реального мира всегда имеет приближенный характер. Если мы, например, поставим вопрос, удовлетворяет ли реальное физическое пространство аксиомам геометрии Эвклида, то предварительно мы должны дать физическое определение геометрических терминов, содержащихся в аксиомах, как то: "точка", "прямая", "плоскость" и др., т.е. указать те физические обстоятельства, которые этим терминам соответствуют. После этого аксиомы превратятся в физические утверждения, которые можно подвергнуть экспериментальной проверке. После такой проверки мы можем ручаться, за истинность наших утверждений с той точностью, какую обеспечивают измерительные приборы [17].
В общем случае интерпретации систем аксиом черпаются из круга математических понятий. Самым мощным источником интерпретаций для всевозможных систем аксиом является теория множеств. Однако и здесь возникает вопрос: является ли теория множеств вполне надежным основанием для аксиоматического метода? На этот вопрос мы частично ответим, рассмотрев два наиболее важных исчисления – исчисление высказываний и исчисление предикатов, являющихся основой построения современных систем баз знаний [18, 19].
Под высказыванием будем понимать, как и ранее, утверждение, относительно которого в любой момент можно сказать, является оно истинным или ложным, или, по крайней мере, предполагать, что ему может быть приписана такая интерпретация, В 4.1 были изложены основные законы алгебры высказываний, которую мы называем булевой. Здесь мы рассмотрим аксиоматическую логическую систему, адекватную алгебре высказываний и называемую исчислением высказываний (ИВ). Остановимся на ней более подробно, так как исчисление высказываний входит как составная часть во все другие логические исчисления. Описание всякого исчисления заключает в себе описание символов этого исчисления (алфавита), формул, являющихся конечными конфигурациями символов, и после этого определение истинных формул. Зададим алфавит ИВ:

где  переменные высказывания;
переменные высказывания;  логические связки (смысл тот же, что и в алгебре высказываний);
логические связки (смысл тот же, что и в алгебре высказываний);  скобки;
скобки; 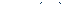 секвенция. Секвенциями называются выражения вида
секвенция. Секвенциями называются выражения вида  (где
(где 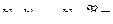 любые формулы).
любые формулы).  где n > 0 ("Из
где n > 0 ("Из 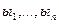 следует
следует  ")
")  ("
("  доказуемо").
доказуемо").  где n > 0 ("система
где n > 0 ("система 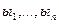 противоречива"). Формулы ИВ представляют собой конечные последовательности символов алфавита. Для обозначения формул будем употреблять большие готические буквы
противоречива"). Формулы ИВ представляют собой конечные последовательности символов алфавита. Для обозначения формул будем употреблять большие готические буквы  Эти буквы не являются символами исчисления. Они представляют собой только условные сокращенные обозначения формул. Полное определение формул имеет рекурсивный характер: указываются некоторые исходные формулы и затем правила, позволяющие из формул образовывать новые формулы. Смысл этого определения состоит в том, что под формулой мы будем понимать такие и только такие строчки, которые могут быть образованы из исходных формул путем последовательного применения указанных в определении правил образования новых формул. Определение формулы:
Эти буквы не являются символами исчисления. Они представляют собой только условные сокращенные обозначения формул. Полное определение формул имеет рекурсивный характер: указываются некоторые исходные формулы и затем правила, позволяющие из формул образовывать новые формулы. Смысл этого определения состоит в том, что под формулой мы будем понимать такие и только такие строчки, которые могут быть образованы из исходных формул путем последовательного применения указанных в определении правил образования новых формул. Определение формулы:
а) переменное высказывание есть формула;
б) если  и
и  – формулы, то строчки
– формулы, то строчки


 (4.16)
(4.16)

также формулы.
В этом определении в а) указываются исходные формулы, которые здесь, представляют собой переменные высказывания. Будем их называть элементарными формулами (атомами). В б) указываются правила, Позволяющие из полученных формул образовывать новые. Таким образом, понятие формулы определено. Приведем примеры.
Переменные высказывания А и В есть формулы в силу а). Следовательно, на основании б) (А→В) и ( 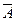
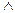 ( А→В))
( А→В))  (А
(А 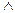 В) также формулы. Чтобы доказать, что приведенная нами для примера строчка есть формула, мы должны рассуждать так. Так как А и В – формулы, то
В) также формулы. Чтобы доказать, что приведенная нами для примера строчка есть формула, мы должны рассуждать так. Так как А и В – формулы, то 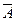 и (А→В) также формулы. Так как
и (А→В) также формулы. Так как 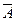 и ( А→В) формулы, то (
и ( А→В) формулы, то ( 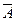
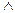 (А→В)) также формула. Так как А и В формулы, то (А
(А→В)) также формула. Так как А и В формулы, то (А 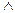 В) также формула. Так как (
В) также формула. Так как ( 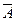
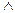 ( А→В)) и (А
( А→В)) и (А 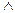 В) формулы, то (
В) формулы, то ( 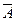
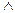 ( А→В))
( А→В))  (А
(А 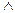 В) также формула. Отсюда видно, что для доказательства того, что данная строчка является формулой, требуется произвести ее конструкцию по указанной выше схеме (а), б)). Так что при построении формулы мы должны построить все ее части. Точное определение части формулы имеет также рекурсивный характер, связанный с операциями, употребляемыми при конструкции формул. Дадим определение части формулы.
В) также формула. Отсюда видно, что для доказательства того, что данная строчка является формулой, требуется произвести ее конструкцию по указанной выше схеме (а), б)). Так что при построении формулы мы должны построить все ее части. Точное определение части формулы имеет также рекурсивный характер, связанный с операциями, употребляемыми при конструкции формул. Дадим определение части формулы.
1. Частью каждой элементарной формулы (атома, переменного высказывания) является только она сама.
2. Допустим, что определены части формул  и
и  . Частями формулы
. Частями формулы  будут все части формул
будут все части формул  и
и  и сама формула
и сама формула 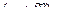
Также определяются части формул 
 и
и  . Если ввести
. Если ввести
ранжирование силы связок (связка 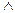 связывает сильнее, чем v, в v
связывает сильнее, чем v, в v
сильнее, чем  , то формулы можно в некоторых случаях писать без скобок (если это не противоречит заданному с помощью cкобок порядку выполнения операций). Так, форму
, то формулы можно в некоторых случаях писать без скобок (если это не противоречит заданному с помощью cкобок порядку выполнения операций). Так, форму 
 будем читать в виде
будем читать в виде 
 .Кроме того, будем опускать внешние скобки. Например, формула
.Кроме того, будем опускать внешние скобки. Например, формула  запишется в виде
запишется в виде  будет правильно построенной формулой (ППФ).
будет правильно построенной формулой (ППФ).
Следующим шагом в описании исчисления высказываний будет выделение некоторого класса формул, которые мы будем называть истинными или выводимыми в исчислении высказываний. Определение истинных формул имеет такой же рекурсивный характер, как и определение формулы. Сначала определяются исходные истинные формулы, а затем правила, позволяющие из имеющихся истинных формул образовывать новые. Эти правила мы будем называть правилами вывода, а исходные истинные формулы – аксиомами. Образование истинной формулы из исходных истинных формул или аксиом путем применения правил вывода будем называть выводом данной формулы из аксиом [17].
Аксиомами исчисления высказываний (ИВ) являются следующие тождественные истинные формулы (тавтологии, формулы, истинные при любых значениях входящих в них высказываний и интерпретированные о помощью таблиц истинности логики высказываний):
1) 
2) 
3) 
4) 
5) 
6) 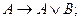
7) 
8) 
9) 
10) 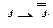
11) 
В исчислении высказываний следует два основных правила вывода.
1. Правило подстановки. Пусть формула  содержит переменное высказывание А. Тогда если
содержит переменное высказывание А. Тогда если  истинная в ИВ формула, то, заменяя в ней букву А всюду, где она входит, правильной формулой
истинная в ИВ формула, то, заменяя в ней букву А всюду, где она входит, правильной формулой  получаем истинную формулу.
получаем истинную формулу.
2. Правило заключения. Если  и
и  истинные формулы в исчислении высказываний, то
истинные формулы в исчислении высказываний, то  также истинная формула.
также истинная формула.
Пример. Покажем, что  истинная в ИВ формула. Возьмем аксиому 5. Заменим А формулой
истинная в ИВ формула. Возьмем аксиому 5. Заменим А формулой  получим истинную формулу
получим истинную формулу  Заменим С на А, получим истинную формулу
Заменим С на А, получим истинную формулу  Видим, что
Видим, что  представляет аксиому 4 и является истинной. Поэтому, применяя правило заключения, получаем истинную формулу
представляет аксиому 4 и является истинной. Поэтому, применяя правило заключения, получаем истинную формулу  Посылка этой формулы
Посылка этой формулы  является аксиомой 3 и поэтому есть истинная формула. Применяя правило заключения, получаем требуемую формулу
является аксиомой 3 и поэтому есть истинная формула. Применяя правило заключения, получаем требуемую формулу 
Из основных правил вывода и аксиом можно вывести ту или иную формулу или ее отрицание. Но вместо того, чтобы истинные формулы в ИВ выводить из аксиом, применяя непосредственно правила вывода, мы изберем более краткий путь, доказав теорему дедукции.
Будем считать, что формула  выводима из формул
выводима из формул  если формулу
если формулу  можно вывести только путем правила заключения (его будем записывать в виде
можно вывести только путем правила заключения (его будем записывать в виде  приняв за исходные формулы
приняв за исходные формулы  и все истинные в ИВ формулы.
и все истинные в ИВ формулы.
Точное определение выводимости формулы  из формул называемых исходными, формулируется следующим образом:
из формул называемых исходными, формулируется следующим образом:
а) каждая формула  выводима из формул
выводима из формул 
б) каждая истинная в ИВ формула выводима из 
в) если формулы  и
и  выводимы из
выводимы из  то формула
то формула  также выводима из
также выводима из 
Утверждение, что формула  выводима из
выводима из  будем записывать с помощью секвенций [17]:
будем записывать с помощью секвенций [17]:

Теорема дедукции: если формула  выводима из формул
выводима из формул  то
то  истинная формула. Докажем сначала, что если
истинная формула. Докажем сначала, что если  то
то  На основе индукции можно провести следующие рассуждения. Докажем, что оно верно, если
На основе индукции можно провести следующие рассуждения. Докажем, что оно верно, если  является либо одной из формул
является либо одной из формул  либо истинной формулой ИВ. Случай, когда
либо истинной формулой ИВ. Случай, когда  истинная формула, очевиден. Затем покажем, что если наше утверждение верно для формул
истинная формула, очевиден. Затем покажем, что если наше утверждение верно для формул  и
и  то оно верно для
то оно верно для  Если
Если  совпадает с формулой
совпадает с формулой  то либо
то либо  либо і < n. В первом случае
либо і < n. В первом случае  истинная формула. Поэтому
истинная формула. Поэтому  Пусть і < n, тогда подстановками в аксиому 1 получим
Пусть і < n, тогда подстановками в аксиому 1 получим  последняя формула как истинная формула выводима из формул
последняя формула как истинная формула выводима из формул  Но формула
Но формула  также выводима из формул
также выводима из формул  Поэтому формула
Поэтому формула  выводима из формул
выводима из формул 
Формула

является истинной в ИВ, так как она получается подстановкой в аксиому 2. Поэтому эта формула выводима из  Обе посылки этой формулы выводимы (по условию) из
Обе посылки этой формулы выводимы (по условию) из  Применяя два раза правило заключения, мы получаем формулу
Применяя два раза правило заключения, мы получаем формулу  , которая, следовательно, также выводима из формул
, которая, следовательно, также выводима из формул  Таким образом, мы доказали, что если
Таким образом, мы доказали, что если  то
то  Это утверждение верно и при h = 1. Теперь, применяя проведенное обозначение еще n – 2 раз (обозначая первый раз
Это утверждение верно и при h = 1. Теперь, применяя проведенное обозначение еще n – 2 раз (обозначая первый раз  через
через 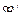

 через
через  и т.д.), получаем
и т.д.), получаем  Но можно применить тоже рассуждение еще раз. Тогда получим
Но можно применить тоже рассуждение еще раз. Тогда получим

чем и доказана теорема дедукции.
С помощью теоремы дедукции довольно несложно доказываются неспорые теоремы, например

Рассмотрим формулы  и
и  Из этих формул только на основании правила заключения можно вывести формулу С. В таком случае, на основании теоремы дедукции заключаем, что
Из этих формул только на основании правила заключения можно вывести формулу С. В таком случае, на основании теоремы дедукции заключаем, что  истинная формула. Теорема доказана.
истинная формула. Теорема доказана.
Если сделаем подстановку в последнюю формулу, заменив А формулой 
 а
а 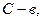 то получим истинную формулу
то получим истинную формулу 
Если формулы  и
и 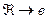 окажутся истинными, то, применяя сложное правило заключения к последней формула, найдем, что формула
окажутся истинными, то, применяя сложное правило заключения к последней формула, найдем, что формула  также истинна. Таким образом, мы получаем правило, которое записывается так:
также истинна. Таким образом, мы получаем правило, которое записывается так:

Это правило носит название правила силлогизма (исключение третьего).
Если обозначить  произвольная секвенции, то в общем случае правилом вывода будет называться выражении вида
произвольная секвенции, то в общем случае правилом вывода будет называться выражении вида
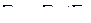 (4.19)
(4.19)
 называется непосредственным следствием
называется непосредственным следствием  по данному правилу вывода.
по данному правилу вывода.
Обозначим  конечные последовательности формул (возможно, пустые), тогда в исчислении высказываний, с учетом расширения алфавита за счет введения секвенций, можно записать следующее производные (сложные) правила вывода [15]:
конечные последовательности формул (возможно, пустые), тогда в исчислении высказываний, с учетом расширения алфавита за счет введения секвенций, можно записать следующее производные (сложные) правила вывода [15]:
1)  (введение
(введение 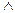 );
);
2)  (удаление
(удаление 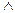 );
);
3)  (удаление
(удаление 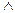 );
);
4)  (введение
(введение  );
);
5)  (введение
(введение  );
);
6)  (удаление
(удаление  );
);
7) 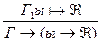 (введение
(введение  );
);
8)  (удаленеие
(удаленеие  );
);
9) 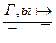 (введение – );
(введение – );
10) 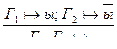 (сведение к противоречию);
(сведение к противоречию);
11)  (удаление –);
(удаление –);
12)  (уточнение);
(уточнение);
13)  (расширение);
(расширение);
14)  (перестановка);
(перестановка);
15)  (сокращение); (4.20)
(сокращение); (4.20)
Таким образом, вывод в ИВ с секвенцией есть конечная последоваельность секвенций  i такая, что для каждого
i такая, что для каждого  есть либо аксиома, либо непосредственное следствие предыдущих секвенций по правилам 1-15. Секвенция
есть либо аксиома, либо непосредственное следствие предыдущих секвенций по правилам 1-15. Секвенция  называется выводимой в ИВ, если существует вывод в ИВ, оканчивающийся
называется выводимой в ИВ, если существует вывод в ИВ, оканчивающийся 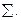
Одной из важнейших теорем, используемой при автоматизации вывода, является теорема эквивалентности: пусть формула (А) содержит переменные высказывания А и пусть формулы  , и
, и  эквивалентны. Тогда формулы
эквивалентны. Тогда формулы  и
и  получаемые из
получаемые из  заменой А соответственно на
заменой А соответственно на  и
и  также эквивалентны. Точнее
также эквивалентны. Точнее
 (4.21)
(4.21)
Полное доказательство этой теоремы дано в [9, 17].
Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого необходимо трактовать свободные переменные исчисления высказываний как переменные алгебры высказываний, т.е. переменные в содержательном смысле принимающие значения И и Л (1 и 0). Операции  определяются так же, как в алгебре высказываний, тогда всякая формула при любых значениях переменных сама будет принимать одно из значений И или Л (1 или 0), вычисляемое по правилам алгебры высказываний. Все аксиомы ИВ при этом будут всегда принимать значение "истина" (1).
определяются так же, как в алгебре высказываний, тогда всякая формула при любых значениях переменных сама будет принимать одно из значений И или Л (1 или 0), вычисляемое по правилам алгебры высказываний. Все аксиомы ИВ при этом будут всегда принимать значение "истина" (1).
При рассмотрении любого исчисления возникает проблема непротиворечивости – одна из кардинальных проблем математической логики [9, 17].
Логическое исчисление называется непротиворечивы, если в нам не выводимы никакие две формулы, из которых одна является отрицанием другой. Иными словами, непротиворечивое исчисление – это такое исчисление, что, какова бы ни была формула  , никогда формулы
, никогда формулы  и
и  не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил. Имеет место теорема: исчисление высказываний непротиворечиво. Как мы уже говорили выше, каждую формулу ИВ можно рассматривать в то же время как формулу алгебры высказываний. Покажем, что все формулы, выводимые в ИВ и рассмотренные как формулы алгебры высказываний, являются тождественно истинными, т.е. принимают значение И при всех значениях переменных. Легко непосредственно проверить, что аксиомы исчисления высказываний таковы. Покажем, что если формула
не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил. Имеет место теорема: исчисление высказываний непротиворечиво. Как мы уже говорили выше, каждую формулу ИВ можно рассматривать в то же время как формулу алгебры высказываний. Покажем, что все формулы, выводимые в ИВ и рассмотренные как формулы алгебры высказываний, являются тождественно истинными, т.е. принимают значение И при всех значениях переменных. Легко непосредственно проверить, что аксиомы исчисления высказываний таковы. Покажем, что если формула  содержащая переменное А, тождественно истинна, то и формула
содержащая переменное А, тождественно истинна, то и формула 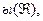 получаемая из
получаемая из  подстановкой, также тождественно истинна. В самом деле,
подстановкой, также тождественно истинна. В самом деле,  при всех значениях переменной принимает значение И(1). В таком случае ы(И) и ы(Л) имеют значение И, каковы бы не были значения других переменных. Но
при всех значениях переменной принимает значение И(1). В таком случае ы(И) и ы(Л) имеют значение И, каковы бы не были значения других переменных. Но  при любых, значениях переменных может иметь только значение И или Л. Отсюда следует, что ы(
при любых, значениях переменных может иметь только значение И или Л. Отсюда следует, что ы(  ) всегда будет иметь значение И.
) всегда будет иметь значение И.
Докажем, что если формулы ы и ы  тождественно истинны, то формула
тождественно истинны, то формула  также тождественно истинна. Если (ы тождественно истинна, то она всегда имеет значение И. Так как ы
также тождественно истинна. Если (ы тождественно истинна, то она всегда имеет значение И. Так как ы  всегда принимает значение И, то
всегда принимает значение И, то  не может принять значение Л ни при каких значениях переменных, иначе формула
не может принять значение Л ни при каких значениях переменных, иначе формула  приняла бы значение И→Л, которое,по определению следования в алгебре высказываний, есть Л.
приняла бы значение И→Л, которое,по определению следования в алгебре высказываний, есть Л.
Итак, мы показали, что:
– все аксиомы тождественно истинные формулы;
– применяя к тождественно истинным формулам правила вывода, мы получаем такие тождественно истинные формулы.
Отсюда следует, что все выводимые формулы исчисления высказываний, рассматриваемые как формулы алгебры высказываний, являются тождественно истинными. В таком случае, если формула ы выводима в исчислении высказываний, то формула  не может быть выводима, так как ы – тождественно истинная формула, a
не может быть выводима, так как ы – тождественно истинная формула, a  тогда, наоборот, принимает значение Л при всех значениях входящих переменных.
тогда, наоборот, принимает значение Л при всех значениях входящих переменных.
При доказательстве непротиворечивости ИВ показано, что всякая формула, выводимая в ИВ, является тождественно истинной, если ее рассматривать как формулу алгебры высказываний. Возникает обратный вопрос: будет ли всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний. Этот вопрос и представляет собой проблему полноты в широком смысле для исчисления высказываний, которая решается положительно для ИВ. Не менее важное значение, чем понятие полноты в широком смысле, имеет понятие полноты логического исчисления в узком смысле. Логическое исчисление называется полным в узком смысле, если присоединение к его аксиомам какой-нибудь не выводимой в нем формулы приводит к противоречию. Исчисление высказываний полно в узком смысле.
Как уже говорилось, всякое логическое исчисление может быть задано следующим образом: задается алфавит, определяется понятие формулы и истинной формулы. Это делается путем указания, во-первых, некоторых исходных формул, объявленных истинными и называемых аксиомами и, во-вторых, правил вывода, с помощью которых из истинных формул можно образовывать новые истинные формулы. Для всякого такого исчисления возникает вопрос о независимости его аксиом. Вопрос этот ставится следующим образом: логично ли какую-нибудь аксиому вывести из остальных, применяя правила вывода данной системы? Показано [17], что система аксиом исчисления высказываний независима, т.е. ни одна из аксиом не может быть выведена из других.
Несмотря на такую строгость и замкнутость исчисления высказываний, оно оказывается недостаточным для задания более сложных логических рассуждений, встречающихся при описании реальных ситуаций, особенно при построении систем автоматического вывода. Более полным исчислением, позволяющим решать ряд задач при построении баз знаний, является следующее исчисление – исчисление предикатов (ИП).
Исчисление предикатов включает в себя исчисление высказываний и позволяет устанавливать новые свойства через введение функций на бесконечных, в общем случае, множествах предметов. Функция F, принимающая одно из значений 0 или 1, аргументы которой пробегают значения из произвольного множества М, называется предикатом. Предикаты, зависящие от одного аргумента х – F(х), описывают свойства предмета и по существу не отличаются от элементарных высказываний. Например, F(x), "х – простое число". F(x) принимает значение 1 (истина) или 0 (ложь) в зависимости от того, что подставим вместо х; F(1) – истина, F(8) – ложь. Предикаты от двух переменных задают взаимоотношения двух предметов F(x, y). Например, F(x,у):х > у. Если взять х = 5, у = 2, F (5,2) = 1; х= 5, у = 10, F(5, 10) = 0.
Предикаты от трех и более переменных могут задавать отношения, существующие между тремя и более предметами, например:
1) х – сын, у – отец, z – дед, F(x , y , z) = x есть сын у и внук z или
2) F(x , y , z) = x + y = z или
3) F(x , y , z , u , v) = x + y + z + u + v = 50.
Истинность или ложность предиката как функции зависит от того, какие конкретные значения примут переменные. Предикат можно, таким образом .трактовать как n-арное отношение в множестве М. Предикат  если
если  находится в отношении R , определяемом этим предикатом;
находится в отношении R , определяемом этим предикатом;  то эти элементы не находятся в отношении
то эти элементы не находятся в отношении  .
.
Из приведенного понятия предиката как функции, определенной на произвольном множестве М и принимающей два значения И или Л (1 или 0), видно, что введенное понятие позволяет свести большое количество отношений реального мира к понятию предиката. Зададим исчисление предикатов как аксиоматическую систему аналогично исчислению высказываний.
Рассмотрим алфавит исчисления предикатов:

 предметные переменные;
предметные переменные;
 предметные символы;
предметные символы;
 функциональные символы;
функциональные символы;
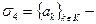 предметные константы;
предметные константы;
 логические символы;
логические символы;
 вспомогательные символы;
вспомогательные символы;
 секвенция.
секвенция.
Выражение  назовем сигнатурой. Дадим определение терма сигнатуры:
назовем сигнатурой. Дадим определение терма сигнатуры:
1. Всякая предметная переменная или предметная константа – терм.
2. Если f – функциональная буква и  – термы, то
– термы, то  – терм. Атомарной формулой сигнатуры
– терм. Атомарной формулой сигнатуры  назовем произвольное слово
назовем произвольное слово  где
где  – n-мерный предикатный символ из
– n-мерный предикатный символ из  ,
,  – термы сигнатуры
– термы сигнатуры  .
.
Дадим определение новым логическим символам  которые называются кванторами существования и всеобщности соответственно и служат для упрощения структуры сложных логических рассуждений. Условимся обозначать выражение "для всякого элемента
которые называются кванторами существования и всеобщности соответственно и служат для упрощения структуры сложных логических рассуждений. Условимся обозначать выражение "для всякого элемента  свойство R выполнено" как
свойство R выполнено" как  а выражение "существует, по крайней мере, один элемент
а выражение "существует, по крайней мере, один элемент  , обладающий свойством R" – как
, обладающий свойством R" – как 
После этого можно ввести понятие формулы:
1. Атомарная формула есть формула.
2. Если ы и  – формулы, то
– формулы, то  формулы.
формулы.
3. Если  формула, а х – предметная переменная, то
формула, а х – предметная переменная, то  формулы.
формулы.
В выражении  формула
формула  называется областью действия квантора
называется областью действия квантора 
Вхождение переменной х в формулу называется связанным, если оно находится в области действия квантора  или
или  и свободным в противном случае. Областью действия кванторов
и свободным в противном случае. Областью действия кванторов  или
или  для формул
для формул  является формула
является формула  Для формулы
Для формулы  областью действия квантора
областью действия квантора  являетоя формула
являетоя формула  а для квантора
а для квантора 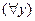 формула
формула  . Если взять формулу
. Если взять формулу  то областью действия квантора
то областью действия квантора  будет формула
будет формула  а областью действия
а областью действия  как и ранее, формула
как и ранее, формула 
Формула ы называется замкнутой формулой или предложением, если всякое нахождение переменной в ы является связанным. Формула ы сигнатуры  назовем тождественно истинной (или тавтологией), если ы истинна при любых значениях свободных переменных. Часть формулы определяется в исчислении предикатов аналогично определению в исчислении высказываний. Будем говорить, что формула ы семантически следует из множества формул Г (символически Г
назовем тождественно истинной (или тавтологией), если ы истинна при любых значениях свободных переменных. Часть формулы определяется в исчислении предикатов аналогично определению в исчислении высказываний. Будем говорить, что формула ы семантически следует из множества формул Г (символически Г  ы), если для любой алгебраической системы m из истинности в m всех формул из Г при некоторых значениях переменных следует истинность ы в m при тех же значениях переменных. В ИП, как и в ИВ, вводится система аксиом:
ы), если для любой алгебраической системы m из истинности в m всех формул из Г при некоторых значениях переменных следует истинность ы в m при тех же значениях переменных. В ИП, как и в ИВ, вводится система аксиом:
1) 
2) 
3) 
4) 
5)  (4.22)
(4.22)
6) 
7) 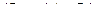
8) 
9) 
10) 
11) 
12) 
В аксиомах А, В, С – любые формулы. В аксиомах 11, 12 F(х) – формула, t – терм, свободный для х в F(x), F(t) – формула, полученная из F(x) заменой всех свободных вхождений х на t.
В связи с введением кванторов для того, чтобы построенные формулы были правильно построенными формулами (ППФ), необходимо:
а) в формуле свободные и связанные переменные обозначать разными буквами;
б) если какой-либо квантор находится в области действия другого квантора, то переменные, связанные этими кванторами, обозначать разными буквами.
Кванторы  и
и  являются двойственными друг другу и могут быть выражены один через другой:
являются двойственными друг другу и могут быть выражены один через другой:

 (4.23)
(4.23)
Как и в случае исчисления высказываний, в исчислении предикатов вовводятся два основных правила вывода, позволяющие получать истинные формулы. Этими правилами являются правило заключения и правило подстановки. Правило заключения: если G и G → H – истинные формулы, то Н – также истинная формула. Правило подстановки в связи с наличием кванторов, связанных и свободных переменных, значительно сложнее правила подстановки исчисления высказываний. Поэтому рассмотрим правило подстановки в переменное высказывание и переменный предикат. В исчислении высказываний формула, в которой замещается переменной высказывание в истинной формуле, могла быть произвольной, здесь необходимо наложить некоторые дополнительные условия на эти формулы, так как иначе в результате подстановки может получиться выражение, даже не являющееся формулой [17, 18].
Замещение перешнного высказывания. Пусть формула 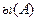 содержит, переменное высказывание А. Тогда мы можем заменить в формуле ы букву А всюду, где она входит, любой формулой G, удовлетворяющей следующим условиям:
содержит, переменное высказывание А. Тогда мы можем заменить в формуле ы букву А всюду, где она входит, любой формулой G, удовлетворяющей следующим условиям:
1. Свободные переменные в G обозначены буквами, отличными от связанных переменных в ы, и связанные переменные в G – буквами, отличными от свободных переменных в ы .
2. Если А в ы находится в области действия квантора, обозначенного какой-то буквой, то эта буква не входит в G. Такое замещение называется подстановкой формулы G в переменное А.
Пример. Пусть 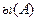 есть формула
есть формула

В таком случае А нельзя заменить формулой  или формулой
или формулой  так как при таком замещении не соблюдено условие 2. Если все же произвести это замещение, то полученная строчка не будет формулой, так как в ней два квантора, один из которых находится в области действия другого, обозначены одинаковыми буквами. Замещение буква А формулой
так как при таком замещении не соблюдено условие 2. Если все же произвести это замещение, то полученная строчка не будет формулой, так как в ней два квантора, один из которых находится в области действия другого, обозначены одинаковыми буквами. Замещение буква А формулой  возможно, так как в этом случае условия 1, 2 выполнены. Полученная в результате такого замещения строчка
возможно, так как в этом случае условия 1, 2 выполнены. Полученная в результате такого замещения строчка


является формулой.
Замещение переменного предиката. Пусть формула  содержит переменный предикат F от n переменных и пусть имеется формула
содержит переменный предикат F от n переменных и пусть имеется формула  содержащая n свободных переменных
содержащая n свободных переменных  (вообще говоря,
(вообще говоря,  может содержать и другие переменные), где
может содержать и другие переменные), где  буквы, отличные от всех предметных переменных формулы ы . Если для формулы
буквы, отличные от всех предметных переменных формулы ы . Если для формулы  соблюдено условие I и еще условие:
соблюдено условие I и еще условие:
3. Если F в ы находится в области действия квантора, связивающего какую-либо букву, то эта буква не входит в  то возможна подстановка формулы
то возможна подстановка формулы  в ы вместо предиката F. Операция подстановки формулы
в ы вместо предиката F. Операция подстановки формулы  в формулу ы(F) вместо F (...) представляет собой замещение каждой элементарной формулы вида
в формулу ы(F) вместо F (...) представляет собой замещение каждой элементарной формулы вида  (где
(где  _ какие-то переменные, не обязательно различные), входящей в ы, выражением, полученным из
_ какие-то переменные, не обязательно различные), входящей в ы, выражением, полученным из  переименованием переменных
переименованием переменных  буквами
буквами  соответственно, При этом иолжно быть жестко указано, какому из переменных
соответственно, При этом иолжно быть жестко указано, какому из переменных  соответствует пустое место в F (...).
соответствует пустое место в F (...).
Пример. Пусть формула ы имеет вид  Требуется произвести подстановку, заменив F формулой (
Требуется произвести подстановку, заменив F формулой (  Пусть при этом первое пустое место в F(...) соответствует переменному t1, в второе – t2. Условия 1 и 3 здесь выполнены, и результатом подстановки будет формула
Пусть при этом первое пустое место в F(...) соответствует переменному t1, в второе – t2. Условия 1 и 3 здесь выполнены, и результатом подстановки будет формула

Рассмотрим еще два важных правила: замены свободного предметного переменного и переименование связанных предметных переменных. Пусть формула ы является истинной формулой в ИП и формула ы/ получена из ы замещением любого свободного предметного переменного другим свободным предметным переменным так, что замещаемое переменное заменяется одинаковым образом всюду, где оно в формулу ы входит; тогда ы/ является истинной формулой исчисления предикатов.
Пример. Рассмотрим формулу

Произведем в ней подстановку в переменное у. Заменив его переменным z, получим формулу

Если формула ы является истинной формулой ИП, то формула ы' полученная из ы замещением связанных переменных другими связанными переменными, отличными от всех свободных переменных формулы ы, также является истинной формулой. При этом замещаемое связанное переменное в формуле ы должно заменяться одинаковым образом всюду в области действия квантора, связывающего данное переменное, и в самом кванторе.
Операция переименования связанных переменных существенно отличается от операции подстановки в свободные переменные. Производя переименование связанных переменных, мы уже не обязаны переименовывать их всюду, где они входят в формулу ы, а лишь только в области действия квантора, связывающего данное переменное. Это значит, что такие одинаковые переменные, для которых связывающие их кванторы имеют области действия, не входящие одна в другую, могут переименовываться разным образом или одно из них может переименовываться, а другое нет.
Пример. Рассмотрим формулу

Применяя операцию переименования связанных переменных, мы можем


С учетом расширения алфавита исчисления высказываний ввдением секвенций обощенные правила вывода исчисления высказываний с секвенцией формулы (4.20) в исчислении предикатов с секвенцией дополняются следующими правилами вывода [14]:
16)  (введение
(введение  );
);
17)  (удаление
(удаление  );
);
18)  (введение
(введение  );
);
19)  (удаление
(удаление  ). (4.24)
). (4.24)
Здесь ы (t) получается из ы (х) заменой всех свободных вхождений х на t ; Г4 – конечная последовательность формулы, не содержащая х свободно; Д – формула, не содержащая х свободно; Г – конечная последовательность формул, возможно пустая.
Формулы (4.20) исчисления высказываний полностью входят в число формул ИП, Правила 16, 18 формул (4.24) обычно называются правилами связывания квантором [17, 20, 21].
Вопрос о непротиворечивости исчисления предикатов легко решается в положительном смысле. В отличие от исчисления высказываний исчисление предикатов является неполным в узком смысле, что легко доказывается, если интерпретировать квантор существования как конечную или бесконечную дизъюнкцию (в зависимости от мощности множества, на котором определены' предикаты), а квантор всеобщности-как конечную или бесконечную конъюнкцию. Например, для множества 

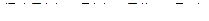
Исчисление предикатов является основой при создании баз знаний и основ автоматического вывода. Рассмотрим прикладные вопросы ИВ и ИП при представлении знаний и в автоматическом выводе.
Модели представления знаний
В настоящее время наиболее перспективными решателями экспертных систем считаются системы, созданные на основе дедуктивных и индуктивных схем рассуждения, метода программируемых доказательств и интегральный подход, позволяющий использовать для решения одного и того же класса задач несколько методов одновременно.
К дедуктивным подходам относится прежде всего логическое программирование, в котором для представления знаний используется формальный аппарат исчисления предикатов первого порядка и его расширение. Под исчислением (или дедуктивной системой) понимается система, в которой существует некоторое число исходных объектов (аксиом) и некоторое число правил построения (правил вывода) новых объектов из исходных и уже построенных. При этом в исчислениях (в отличие от алгоритмов) порядок применения правил вывода может быть произвольным. Можно считать, что исчисление предикатов является расширением классического исчисления высказываний, в котором высказывание рассматривается как единое целое, не обладающее внутренней структурой, а истинность или ложность высказываний фиксирована. В исчислении предикатов, как было показано, основным объектом является переменное высказывание (предикат), истинность или ложность которого зависит от значений входящих в него переменных. Для обозначения области значений, как известно, используются два квантора –квантор всеобщности  и квантор существования
и квантор существования  Как известно, в исчислении высказываний формулы строятся индуктивным способом с помощью связок
Как известно, в исчислении высказываний формулы строятся индуктивным способом с помощью связок  (дизъюнкция, конъюнкция, отрицание, импликация). Исчисление предикатов включает в себя все формулы исчисления высказываний, а также формулы, содержащие кроме символов высказываний предикатные символы с кванторами. Выделенное подмножество тождественно истинных формул, истинность которых не зависит от истинности входящих в них высказываний, называется аксиомами. Они были приведены в 4.4.
(дизъюнкция, конъюнкция, отрицание, импликация). Исчисление предикатов включает в себя все формулы исчисления высказываний, а также формулы, содержащие кроме символов высказываний предикатные символы с кванторами. Выделенное подмножество тождественно истинных формул, истинность которых не зависит от истинности входящих в них высказываний, называется аксиомами. Они были приведены в 4.4.
Как известно, за исключением двух последних все остальные аксиомы являются аксиомами исчисления высказываний. В исчислении предикатов имеется множество правил вывода. Основными из них являются правило заключения (модус поненс) и правило подстановки. При использовании формул логики предикатов совсем не обязательно ограничиваться какой-то определенной формой описания для выражения смысла высказываний. Здесь имеется возможность различных представлений, что зависит от взглядов конкретного человека. Такое многообразие соответствует многообразию оборотов речи в естественном языке. Знания, которые могут быть представлены с помощью логики предикатов, являются фактами, представляемыми логическими формулами. Для представления какой-либо области в виде логических формул прежде всего необходимо выбрать константы, которые определяют объекты в данной области, а также функциональные символы и предикатные символы, которые определяют соответственно функциональную зависимость и отношения между объектами. Символы других типов являются общими и не зависят от конкретного мира [21].
Следовательно, определив константы, функциональные и предикатные символы, можно построить логические формулы, описывающие данную область. Записать знания в виде логических формул не удается в тех случаях, когда затруднен выбор указанных трех групп символов или же когда эти знания превышают возможности представления в логике предикатов.
Автоматическое преобразование предложений, написанное на естественном языке, в язык формальных систем типа логики предикатов. называется пониманием естественного языка. Это очень сложная проблема, и удалось в ней добиться лишь частичных результатов. При трансляции, помимо выбора трех символов, возникает проблема, касающаяся и логических символов. Примером тому является символ V. B интерпретации логики высказывания выражение Р "или" Q допускает, что и Р и Q могут быть истинными. В данном случае "или" называется "неразделительное или". Если одно из выражений Р и Q – истина, а другое ложь, то "или" называется "исключающее или". В естественном языке "или" может употребляться как в значении "неразделитвльное или", так и в значении "исключающее или". Например, в предложении "все люда являются мужчинами или женщинами" "или" интерпретируется как исключающее "или". Поскольку V означает неразделительное или, то для того, чтобы в выражении Р или Q "или" имело смысл "исключающее или", следует записать, например,

Еще одна проблема связана с символом →. Р → Q имеет такой же смысл, как и  v Q, например "если 5x5=30, то все компьютеры имеют одинаковое быстродействие" интерпретируется как истина. И все же, обычное предложение вида Р → Q показывает причинно-следственные связи между Р и Q , и если в логике предикатов и в логике высказываний отбросить смысл предикатных символов, то теряется связь со смыслом Р и Q, поэтому такое отношение выходит за рамки логики предикатов.
v Q, например "если 5x5=30, то все компьютеры имеют одинаковое быстродействие" интерпретируется как истина. И все же, обычное предложение вида Р → Q показывает причинно-следственные связи между Р и Q , и если в логике предикатов и в логике высказываний отбросить смысл предикатных символов, то теряется связь со смыслом Р и Q, поэтому такое отношение выходит за рамки логики предикатов.
Будем предполагать, что при описании конкретной ситуации в виде логической формулы были использованы связки  и кванторы и получена правильно построенная формула (ППФ). Для удобства машинного вывода ее надо представить в так называемой префиксной нормальной форме. Для начала научимся исключать из ППФ связки → и
и кванторы и получена правильно построенная формула (ППФ). Для удобства машинного вывода ее надо представить в так называемой префиксной нормальной форме. Для начала научимся исключать из ППФ связки → и  По определению, эти связки могут быть следующим образом представлены через оставшиеся три связки:
По определению, эти связки могут быть следующим образом представлены через оставшиеся три связки:


Если теперь воспользоваться этими выражениями, то во всех комбинациях ППФ можно ограничиться только тремя связками. Предикат, не содержащий переменных, аналогичен высказыванию, поэтому такие предикаты будем обозначать просто как F и G. Когда некоторое отношение выполняется для любого квантора (  или
или  ), то сложно описывать эти два отношения, вводя каждый раз
), то сложно описывать эти два отношения, вводя каждый раз  V и
V и  , поэтому такой случай принято записывать как Qx:
, поэтому такой случай принято записывать как Qx:

 (4.25)
(4.25)
Эта пара формул показывает, что «высказывание не имеет отношения к квантору переменной, которая включена в другой предикат». Рассматрим важнейшие соотношения ИП. Согласно принципу двойственности имеем




 (4.26)
(4.26)
Чтобы в этом убедиться, обратимся к простому примеру. Положим, что областью изменения х является множество  При этом допустим, что истинной является только F(a), F(б), H(в). Тогда левая часть первой формулы не выполняется, а ее правая часть является истиной. Следовательно, левая и правая части не равны. И обратно, если левая часть выполняется, то ясно, что непременно выполняется и правая часть, т.е. для формулы справедливо не равенство, а связка →:
При этом допустим, что истинной является только F(a), F(б), H(в). Тогда левая часть первой формулы не выполняется, а ее правая часть является истиной. Следовательно, левая и правая части не равны. И обратно, если левая часть выполняется, то ясно, что непременно выполняется и правая часть, т.е. для формулы справедливо не равенство, а связка →:
 (4.27)
(4.27)
Для второй формулы аналогично, если обратиться к тому же примеру и принять, что справедливо только F(a) и Н(б), то левая часть будет истиной, а правая часть не выполняется. Далее, если справедлива правая часть, то непременно справедлива и левая, поэтому выполняется
 (4.28)
(4.28)
Итак, непосредственно саму по себе нельзя получить префиксную формулу. Ее удается построить введением новых переменных. Смысл последних двух формул в том, что описание для двух разделенных предикатов не совпадает с описанием, использующим эти предикаты одновременно как единое целое и с одинаковыми переменными. Поскольку диапазон изменения переменных, входящих в предикаты, лежит внутри этого объединенного предиката, то на практике в этих двух формулах можно, изменив все переменные в их правых частях, записывать в следующем виде:

 (4.29)
(4.29)
В правых частях этих формул предикат Н (у) не содержит переменной х и в этом смысле, так же, как и высказывание, не зависит связывания х, поэтому формулы можно переписать в следующем виде:
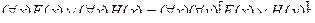
 (4.30)
(4.30)
В конечном итоге для этого случая необходимо вводить новые переменные. Описанное правило рассматривалось применительно к предикатам одной переменной; при получении многих переменных его можно использовать последовательно к каждой из них [21].
Если упорядочить процесс получения префиксной нормальной формы, то он будет выглядеть следующим образом:
1) используя формулы  заменяем
заменяем  и
и  на
на 
2) воспользовавшись выражениями 

 (правила де Моргана) (4.31)
(правила де Моргана) (4.31)
предикатные формулы можно преобразовать так, что символы отрицания будут вынесены перед символами предикатов.
3. Вводятся новые переменные для формулы (4.26).
4. Используя формулы (4.26) – (4.30), получают представления формул в префиксной нормальной форме.
В качестве примера рассмотрим следующее выражение А, которое надо привести к префиксной нормальной форме, т.е. чтобы все кванторы были перед правильно построенной формулой, а не внутри:
 (4.32)
(4.32)
В соответствии с изложенной процедурой А будет преобразовано следующим образом:
Из 1): 
Из 2): 
Из формулы (4.26) 
Из формулы (4.26) 
После того как рассмотренными процедурами кванторы будут вине сены в префиксную часть формулы, проводятся дальнейшие преобразования. Эти преобразования позволяют полностью исключить из префиксных формул кванторы, с тем, чтобы обеспечить дальнейшее упрощение логических представлений и обеспечить введение процедур машинной обработки в логику предикатов.
Конечно, использование кванторов является неотъемлемым условием правильного отражения семантики языка предикатов, и поэтому, прежде чем их исключать, необходимо выполнить надлежащие процедуры, которые позволят полностью сохранить семантику. Процедуры такого рода вводятся через понятие сколемовской функции. Для описания той функции рассмотрю следующий простой пример.  образует резьбовое соединение (х, у): для каждого х (болта) существует у (гайка), такой, что х образует соединение с у. Это означает, что если выделить один конкретный х (болт), то дал этого х существует у, удовлетворяющий функции "образует резьбовое соединение (х, у.)". Иными словами, у зависит от х или же у, должен определяться в зависимости от х. Это отношение х и у, может рассматриваться как своеобразное функциональное отношение в том смысле, что если задано х, то существует и соответствующий ему у (может быть, подбираемое по ГОСТу или таблицам метрических или дюймовых резьб).
образует резьбовое соединение (х, у): для каждого х (болта) существует у (гайка), такой, что х образует соединение с у. Это означает, что если выделить один конкретный х (болт), то дал этого х существует у, удовлетворяющий функции "образует резьбовое соединение (х, у.)". Иными словами, у зависит от х или же у, должен определяться в зависимости от х. Это отношение х и у, может рассматриваться как своеобразное функциональное отношение в том смысле, что если задано х, то существует и соответствующий ему у (может быть, подбираемое по ГОСТу или таблицам метрических или дюймовых резьб).
Отсюда следует, что у можно заменить на функцию f(x), которая описывает данное отношение. Поскольку функция f(x) возникла в конечном итоге из того обстоятельства, что переменная у проквантифицирована квантором  при подстановке этой функции на место у данный факт будет тем самым отражен, и сам по себе квантор
при подстановке этой функции на место у данный факт будет тем самым отражен, и сам по себе квантор  уже не потребуется. Таким образом, исходную логическую формулу можно будет переписать в виде
уже не потребуется. Таким образом, исходную логическую формулу можно будет переписать в виде  образуется резьбовое соединеннее х, f(x)). Подобная функция называется сколемовской [20].
образуется резьбовое соединеннее х, f(x)). Подобная функция называется сколемовской [20].
Сколемовокая функция необходима дм того, чтобы предикатная формула в качестве своих аргументов включала только те исходные переменные, которые влияют на переменные, связанные квантором существования. Приоритетность действия кванторов, имеющихся в префиксной форме представления, определяется в порядке слева направо. Например, формула  имеет тот смысл, что "для всех х существует некоторый у, такой, что
имеет тот смысл, что "для всех х существует некоторый у, такой, что  истина при всех z", Из этой формулы следует, что переменной, которая влияет на связанную квантором
истина при всех z", Из этой формулы следует, что переменной, которая влияет на связанную квантором  переменную у, является только х; значит, ее логично переписать в следующем виде:
переменную у, является только х; значит, ее логично переписать в следующем виде:

Если входная формула есть  то смысловая формула есть
то смысловая формула есть  Если переменная, связанная квантором существования, является крайней слева, то такую формулу можно заменить функцией без аргументов, т.е. константой.
Если переменная, связанная квантором существования, является крайней слева, то такую формулу можно заменить функцией без аргументов, т.е. константой.
 образует резьбовое соединение (х, у) = образует резьбовое соединение (х, у).
образует резьбовое соединение (х, у) = образует резьбовое соединение (х, у).
Если проделать эту операцию для ранее рассмотренного примера, то получим


В случае, когда в одной логической формуле имеется более двух связанных квантором  переменных, то сколемовская функция также будет распадаться на различные функции. Например:
переменных, то сколемовская функция также будет распадаться на различные функции. Например:

Итак, если подобным образом исключить связанные квантором существования переменные, то любые другие переменные, которые встречаются в формуле, будут связаны только квантором  и поэтому уже не понадобится пояснять это обстоятельство связыванием переменных кванторами. Следовательно, квантор
и поэтому уже не понадобится пояснять это обстоятельство связыванием переменных кванторами. Следовательно, квантор  также можно из формулы исключить. В таком случае, например, формула последнего примера для А примет вид
также можно из формулы исключить. В таком случае, например, формула последнего примера для А примет вид

и можно будет упростить формальное представление без потери информации, содержащейся в исходной формуле. Такого рода формальное представление предикатных формул принято называть сколемовской нормальное формой [17, 21].
Следующим шагом на пути к применению автоматического вывода является переход err полученных в предыдущем разделе результатов к конъюнктивной нормальной форме, а затем – к описанию предикатных формул в форме предложений (клаузальной форме). Обычно предикатная формуле в сколемовской нормальной форме представляет собой несколько предикатов, содержащих переменные и соединенных различными связками. Однако, далее на этом этапе нормализации форма представления одинаковых по смыслу предикатных формул неопределена и все еще остается некоторая произвольность толкования изначально заданных выражений. Например,  означает то же самое, что и
означает то же самое, что и  По смыслу формула совпадает с распределительным законом конъюнкции относительно дизъюнкции:
По смыслу формула совпадает с распределительным законом конъюнкции относительно дизъюнкции:  Используя его и еще соотношения
Используя его и еще соотношения


 (4.32а)
(4.32а)


можно любую логическую формулу автоматически преобразовать к дизъюнктивной. нормальной форме (ДНФ) или конъюнктивной нормальной форме, (КНФ), не теряя при этом ее смысла. Можно получить совершенные СДНФ СКНФ через таблицу истинности.
Использование той или иной нормальной формы зависит от поставленной цели преобразования. Таким же образом и сколемовская нормальная форма может быть преобразована в дизъюнктивную или конъюнктивную нормальную форму. Переход к этим формам позволяет нивелировать произвольность представления, имеющего одинаковый смысл.
В методе автоматического вывода (методе резолюций) сколемовская нормальная форма описывается конъюнктивной нормальной формой. Обычно используется дополнительное приведение к клаузальной форме (форме предложений), которая еще более позволяет упростить способ записи. В клаузальной форме вводится понятие предложения, которым называется часть конъюнктивной нормальной формы, ограниченная скобками ( ) (группа предикатов,связанных через V). Вся исходная логическая формула, представленная в конъюнктивной нормальной форме, объединяется через связки  , как точно такое же предложение.
, как точно такое же предложение.
В группе порознь заданных логических формул каждая входящая в группу формула может быть истинной, поэтому все вместе они могут рассматриваться как единое целое,где формулы соединены через связки  , и наоборот, группы логических формул,соединенных связками
, и наоборот, группы логических формул,соединенных связками  , могут быть представлены в виде отдельных формул. Однако, когда соединяющиеся в некоторой формуле переменные распространяют свое действие на обе части, связанные через
, могут быть представлены в виде отдельных формул. Однако, когда соединяющиеся в некоторой формуле переменные распространяют свое действие на обе части, связанные через  , такое распределение не допускается. Рассмотрим пример:
, такое распределение не допускается. Рассмотрим пример:
 (4.33)
(4.33)
Если проследить операции приведения к нормальной форме в обратном направлении, то получим
 (4.34)
(4.34)
Однако из формул (4.29) и (4.30), которые связывают кванторы и связку  , следует
, следует

Поскольку диапазон действия переменных внутри логической формулы ограничен этими предикатами, то эту формулу можно разделить на две независимые формулы. Если затем снова выполнить операцию приведения к нормальной форме, то это будет аналогично заданию двух формул:
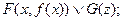
 (4.35)
(4.35)
Поэтому формула (4.33), приведенная к конъюнктивной нормальной форме, будет такой же, что и соответствующие предложения, заданные по отдельности как независимые логические формулы. И наоборот, конъюнктивную нормальную форму для формулы (4.32) можно разложить на предложения. Множество предложений, полученных в результате разложения, называется клаузальным множеством.
В последнее время предметом самого широкого обсуждения в обработке знаний стали предложения Хорна, которые используются в языке логического программирования ПРОЛОГ. Рассмотрим их отношение к логике предикатов первого порядка. Все описанные клаузальные формулы (предложения) представляют собой несколько предикатов, объединенных связкой V. В общем, виде эти формулы содержат предикаты и отрицания предикатов, т.е. клаузальная формула означает то же самое, что и формула вида
 (4.36)
(4.36)
Преобразование в клаузалъную форму соответствует описанию логической формулы самого общего вида группой формул вида (4.36). При атом формулы вида (4.36) в зависимости от величины k и l классифицируются по нескольким типам:
1) тип 1; k = 0, l = 1. Предложение представляет собой единичный предикат, и оно может быть записано как  где
где  являются термами. В случае, когда вое термы константы, они описывают факты, которые 'соответствуют данным, хранящимся в базе данных. Если термы содержат переменные, то они задают общезначимые представления, высказываемые для группы фактов. Например, таким представлением является ИЗМЕНЯЕМОСТЬ (х): "Все течет, все изменяется".
являются термами. В случае, когда вое термы константы, они описывают факты, которые 'соответствуют данным, хранящимся в базе данных. Если термы содержат переменные, то они задают общезначимые представления, высказываемые для группы фактов. Например, таким представлением является ИЗМЕНЯЕМОСТЬ (х): "Все течет, все изменяется".
2) тип 2: k ≥ 1, l = 0.
Этот тип можно записать в виде
 (4.37)
(4.37)
Обычно он используется для описания вопроса. Причиной, по которой данный тип предложения становится вопросом, является то, что ответ на вопрос реализуется в виде процедуры доказательства. Однако для этого доказательства используется так называемый метод опровержения, при котором создается отрицание вопроса и доказывается, что отрицание не выполняется. Такая форма вопроса принимает вид (4.37).
3) тип 3: k ≥ 1, l = 1.
Этот тип соответствует знанию в форме ЕСЛИ - ТО:

4) тип 4: k = 0, l > 1.
Этот тип имеет вид
 (4.37а)
(4.37а)
и используется при представлений фактов, содержащих нечеткости. Обычно нечеткости возникают при неполноте информации. Формула (4.37а) имеет неполную информацию в том смысле, что.из нее нельзя определить, какой из предикатов среди  является истиной.
является истиной.
5) тип 5: k ≥ 1, l > 1.
Это наиболее общий тип, выражаемый формулуй (4.36). Например,к этому типу относятся представления вида
Родители (х, у) → отец (х, у)  мать (х, у).
мать (х, у).
В системе предложений Хорна среди всех перечисленных типов предложений допустимы предложения типа 1, 2, 3, а типы 4 и 5 запрещены. Системы, ограниченные предложениями Хорна, не допускают представлений с использованием типов 4 и 5, однако эти системы сравнительно легки в реализации, и поэтому они нашли самое широкое применение.
Дата добавления: 2018-11-24; просмотров: 1091; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
