Производящие функции для сочетаний и перестановок

⇐ ПредыдущаяСтр 13 из 16Следующая ⇒

Многие комбинаторные задачи на подсчет числа конфигураций могут быть унифицированы б помощью сравнительно простого математического аппарата – производящей функции. Для примера рассмотрим три объекта, обозначенных x ₁ х₂ x ₃. Образуем произведение (l+ x ₁ t) (1+ х₂ t) (1+ x ₃ t).Перемножив и рас-положив это произведение по степеням t, получим 1+(x ₁ + x ₂ + x ₃)t + +(x ₁ x ₂ + x ₁ x ₃ + x ₂ x ₃)t ² + x ₁ x ₂ x ₃ t ³, или 1+a₁t+a₂t²+a₃t³, где a_1,a_2,a₃ - элементарные симметрические функции трех переменных х₁, x ₂ ,х₃. Эти симметрические функции определяются вышеприведенным выражением. Можно заметить, что число слагаемых каждого коэффициента а _r(r=1,2,3) равно числу сочетаний из трех элементов по r. Следовательно, число таких сочетаний получается приравниванием каждого х _i единице, т.е. (1+ t)³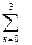⁼ a_r (1,1,1) tⁿ.

Для случая n различных объектов x ₁ , x ₂ ,…, x_n ясно, что

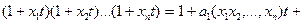
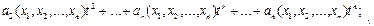
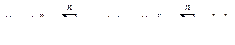(5.9)

Двучлен (1+x_i t) можно интерпретировать как отрезок формального ряда x_i ^○ t ^○ + x_it и сопоставить x_i ^○ отсутствию x_i a x_i - наличию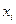

Выражение (1+ t)ⁿ называется перечисляющей производящей функцией сочетаний из n различных объектов, если каждый объект появляется в сочетании не более одного раза. В произведении (1+ x ₁ t)(f + tx ₂)…(1+x_nt) каждый множитель является биномом, который благодаря наличию в нем слагаемых 1 и x_k указывает на возможность наличия или отсутствия в каждом из сочетании элемента x_k. Это произведение порождает сочетания, так как коэффициент при t^r в нем получается выбором единицы в n - r из n двучленных множителей и в r оставшихся после такого выбора множителях – членов вида x_kt всеми возможными путями. Эти коэффициенты по самому их определению являются r-сочетаниями. Каждый элемент в любом сочетании может появляться не более одного раза, ибо любой множитель состоит только из двух слагаемых.

Следовательно, производящую функцию для сочетаний, в которых элементы х _n могут содержаться по 0,1,2,…,j раз, можно получить заменой прежних, множителей множителями вида

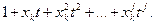(5.10)

Более того, множители производящей функции можно совершенноm независимо друг от друга приспосабливать к любым требованиям задачи. Так, например, если х_k должно всегда входить четное число раз, но не более чем j раз, то j-й множитель (j =2 i +1)следует выбирать в виде 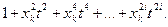Следовательно, производящая функция для любой задачи описывает не только виды элементов, но и вида искомых сочетаний. Множитель 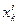в каждом члене коэффициента при соответствующей степени t в выражении производящей функции показывает, что элемент, x_k появляется в соответствующем сочетании i раз. Рассмотрим некоторые примеры. Пусть требуется найти производящую функцию для r-сочетаний с неограниченным повторением из n элементов. Тогда i-й множитель будет иметь вид 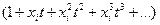отсюда получаем

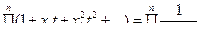(5.11)

Производящая функция получится, если приравнять все x_i =1:

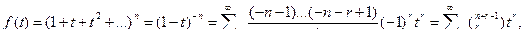(5.12)

где положыли по определению

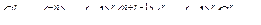
Таким образом,

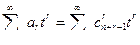(5.13)

Отсюда имеем последовательность b=(b₀,b₁,…) где 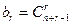- число r-cочетаный с повторениями из n элементов.

Если ввести дополнительное условие непременного вхождения в сочетание по меньшей мере одного элемента каждого вида, перечисляющая производящая функция будет иметь вид;

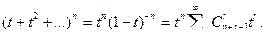(5.14)

Обозначим n+r=k, получим

(5.15)

Следовательно, число искомых r -сочетаний равно 0 при r < n 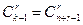и при .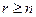

Для сочетаний, допускающих четное число повторений каждого элемента x_i, производящая функция запишется в виде

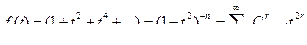
Таким образом, число r-сочетаний при нечетном r равно нулю. Подобные примеры, очевидно, могут быть неограниченно придуманы во всевозможных комбинациях (например, встречаемость каждого элемента по i раз; i = 3,4,5,...; встречаемость первого - i раз, второго - j раз, третьего - k раз и т.д., n – го – р раз). При образовании сочетания осуществляется независимый выбор элементов. И это преимущество используется в производящей функции на основе правила умножения. Действительно, каждый коэффициент произведения является производящей функцией для элементов данного вида.

В случав коммутативных алгебраических операций произведения x ₁ x ₂ и х₂ x ₁одинаковы. Поэтому производящую функцию, описывающую перестановки, невозможно построить, как это было сделано для сочетаний. Однако если учтем, что 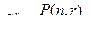то можем записать 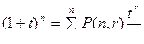т.е. в разложении (1 + t) число r – перстановок P(n , r) является коэффициентами при 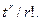Этот факт указывает пути для обобщения. Если какой-либо элемент может проявлятся 0, 1, 2…k раз или если существует k элементов данного вида, то множитель (1 + t) в последней формуле заменяется множителем

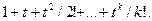
Это объесняется тем, что число перестановок из n элементов, р из которых одного вида, g – другого вида и т.д. равно n!/ p!g!... Это число оказывается коэффициентом при 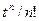в произведении 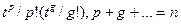, что в точности соответствует требованиям: буква, определяющая элементы второго типа, появляется точно р раз, буква, определяющая элементом второго типа, – ровно g - раз и т.д.

Следовательно, если перестановки заданы условиями, согласно которым k-й из n элементов должен появляться 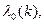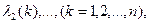то число r -перестановок оказывается коэффициентом при 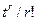в произведении

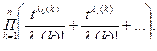(5.16)

Возникающие здесь перечисляющие производящие функции могут быть названы экспоненциальными производящими функциями. Подобный термин оправдан аналогией, ибо известно, что

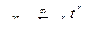(5.17)

Рассмотрим некоторые примеры. Для r-переотановок из n различных элементов с неограниченными повторениями (любой элемент может появляться в перестановке произвольное число раз) перечисляющая роизводящая функция есть.

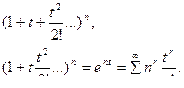(5.18)

Следовательно, число r -перестановок равно n^r .Если каждый элемент входит в перестановку не менее одного раза, то производящая функция примет вид

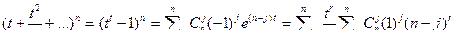(5.19)

Для r-перестановок из n элементов двух типов (p + g = n) производящей функцией будет 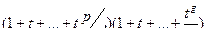. Легко проверить, что коэффициент при 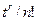есть 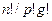. Число r-перестановок является коэффициентом при 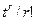. И, наконец, отметим связь перестановок с неограничеными повторениями с задачами на размещения элементов по ячейкам. Для примера рассмотрим восемь 3-перестановок с повторениями из элементов двух типов – а и b. ааа, a а b, а ba , baa , abb , bab , bba . Их можно поставить во взаимно однозначное соответствие с размещениями трех различных элементов по двум ячейкам (ячейки отделены вертикальными черточками): abc/-,ab/c, ас/b, bc/a, a/bc , b/ac , c/ab ,-/ abc. В комбинаторике доказано [24], что число r-перестановок с повторениями из объектов n различных типов равно числу размещений r различных элементов по n различным ячейкам.

Ограничения также взаимно однозначно интерпретируются. Например, "каждая перестановка содержит по меньшей мере по одному элементу каждого типа" соответствует требованию, относящемуся к размещениям: все n ячеек должны оказаться занятыми. Как видно из этих рассуждений, производящая функция является важным средством при исследовании комбинаторных проблем. Действительно, если комбинаторный анализ рассматривать как метод для отыскания коэффициентов при сложных преобразованиях конкретных функций, то и обратно эти функции можно рассматривать как порождающие соответствующие коэффициенты. Уточним введенное неформальное введение производящих функций, сделанное для сочетаний и перестановок.

Обычной производящей функцией для последовательности а₀,а₁,... называется сумма

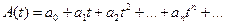. (5.20)

Экспоненциальной производящей функцией для той же самой последовательности называется сумма

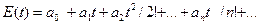(5.21)

Элементы последовательности a _1, a ₂ ... упорядочены, но не обязательно различны. Переменная t производящей функции никак не определена, и ее можно считать абстрактным знаком, роль которого, как и его степеней, сводится лишь к тому, чтобы различать элементы последовательности, объединенные в сумму, определяющую данную производящую функцию. В этом случае переменная t оказывается орудием для алгебраических преобразований над подобными последовательностями элементов. Формальные операции над производящими функциями, такие, как сложение, умножение, дифференцирование и интегрирование по t , помогают сформулировать определения и выявить зависимости в этой алгебре, в частности путем приравнивания коэффициентов при степенях t ⁿ после выполнения этих операций.

Алгебра степенных рядов А(t) называется алгеброй Коши, а алгебра степенных рядов E ( t ) – символическое исчисление Блиссара.Для одной переменой как А( t ), так и Е( t ) явлеются частным случаем выражение

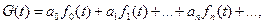(5.22)

для которого единственным требованием является линейная независимость функций 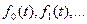(для того чтобы сделать выражение однозначным). Рассмотрим элементарные операции алгебры Коши, задающие соотношения между обычными производящими функциями. Обозначим 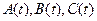производящие функции, соответствующие последовательностям 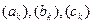. Тогда в качестве непосредственного следствия из самого определения последовательности получаем две пары соотношений; в каждой паре выполнение одного из них влечет за собой выполнение второго. Сумма:

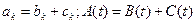(5.23)

Произведение:

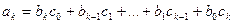
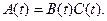(5.24)

Первые соотношения получаются при приравнивании коэффициентов при одинаковых степенях t в обоих частях вторых равентсв.

Особую роль играет выражение 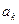в произведении производящих функций которые обычно называют сверткой последовательностей 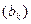и (С_к). Произведение производящих функций находит многочисленные приложения, получаемые путем специализации одной из функций B (t), C (t). Так, например, соотношение 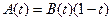означает, что 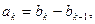или 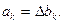Производящая функция последовательности 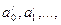обратно к последовательности 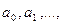определяется условием 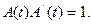Так что

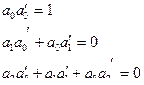(5.26)

Дифференцирование приизводящих функций в алгебре Коши задается следующими простыми выражениями (обозначив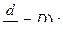

…………..

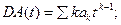
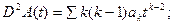
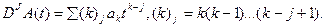(5.27)

Произведение двух обыкновенных производящих функций широко используется при решении линейных рекуррентных уравнений.

Аналогичные (но более сложные) соотношения имеются для экспоненциальных производящих функций в исчислении Блиссара [2], на которых мы не будем останавливаться. Отметим только соотношения между обычными A(t) и экспоненциальными E(t) производящими функциями последовательности Например, для последовательности;

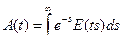(5.28)

Если учесть, что 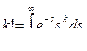(интеграл Эйлера для гамма функции),то

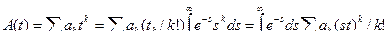(5.29)

Напремер,для последовательности 1= a ₀ = a ₁ =…

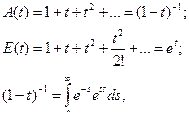(5.30)

Для последовательности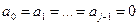

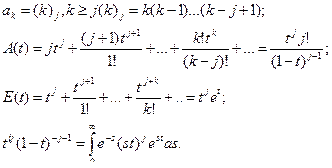(5.31)

Метод включения и исключения

Предположим, что имеется N объектов, из которых N (а) обладают свойством а; если далее 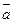означает отсутствие свойства а, то 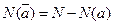.Если рассмотреть объекты, которые могут обладать свойствами а₁, и a ₂ , то число объектов, не обладающих ни одним из них дается формулой

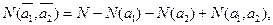(5.32)

так как при вычитани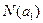и и 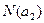из общего количества объектов величина 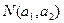вычитается дважды, а поэтому должна быть восстановлена. Этим определяется термин "включение и исключение"; процесс состоит из включения всего и исключения лишнего, во включении ошибочно включенного и т.д., т.е. в попеременном включении и исключении [ 23].

Если свойства 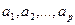взаимно исключающие (несовместные друг с другом), то очевидно

. (5.33)

Когда элементы множества N могут обладать комбинациями совместимых свойств, число элементов, не обладающих ни одним из свойств 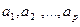дает

Теорема. Если даны N - множество элементов и Р - множество свойств 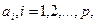то

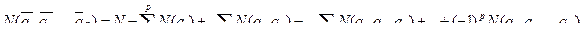(5.34)

Доказательство методом индукции приведено в.[23] . Для того чтобы облегчить всестороннее использование этой теоремы, сделаем следующее замечание. Будем рассматривать отсутствие свойства 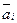и наличие а _i как полную группу событий (в вероятностной трактовке) с точки зрения вероятностной меры, т.е. 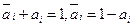. А в выражении N(a_i) букву N будем рассматривать как формальный оператор. Тогда, например. 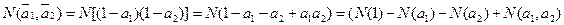,где N(1)=N - общее число объектов.

Для большей формализации примем

(5.35)

Тогда можно определить подмножество объектов из N, обладающих одними свойствами и не обладающих другими свойствами. Например, 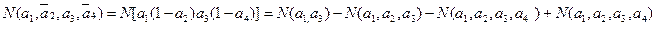Вообще говоря, если n различных свойств 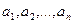объектов из совокупности N обозначить 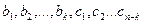,, то получаем формулу

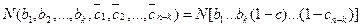(5.36)

Наиболее интересной эта формула оказывается тогда, когда несколько свойств являются совместимыми. Рассмотрим применение этой формулы для решения вероятностных задач. С этой целью (как и ранее) через 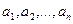обозначим различные свойства и определим величины:

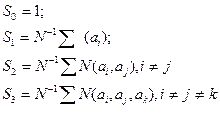(5.37)

В S ₁ входит сумма, взятая по всем n свойствам, в S _2, - по всем парам свойств, в S ₃ - по всем тройкам и ,т.д. Далее, если положить 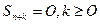формула рассмотренной теоремы примет вид

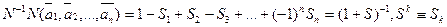(5.38)

Эта вероятностная формула показывает, долю объектов, не обладающих ни одним свойством a_i и может быть заменена Р(0). в тех же самых обозначениях P(k) является относительным числом объектов, обладающих в точности k свойствами из данных n свойств, причем из 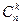сочетаний свойств берутся только k-сочетания совместныхсвойств. Таким образом,

, (5.38а)

если сумма берется по всем совместным сочетаниям из n свойств по k. Заметим, что для упрощения обозначений под знаком суммы записан первый, а не общий член этой суммы. Теперь

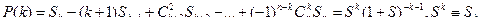(5.39)

Появление биноминальных коэффициентов объясняется тем, что, например, выражение 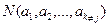появляется столько раз, сколько имеется k-сочетаний из k + j элементов.

Будем рассматривать 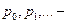последовательность вероятностей (распределение вероятностей), 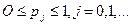.Обычные моменты этого распределения определяются как

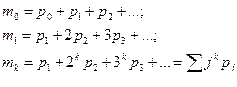(5.40)

Факториальные моменты определяются соотношениями

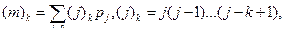(5.41)

а тесно связанные с ними биноминальные моменты – соотношениями

Обозначения (m)_k приняты для факториальных моментов вследствие того, что 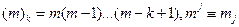- обычный момент .

Центральные моменты определяются так:

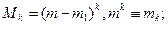(5.43)

В частности, второй центральный момент 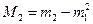называется дисперсией. Все производящие функции определенных выше моментов взаимосвязаны. Пусть P(t) - обычная производящая функция для указанного выше распределения вероятностей, т.е.

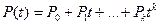(5.44)

Тогда

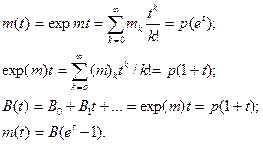(5.45)

Все эти зависимости получаются путем формальных операций! Второе соотношение из последней группы формул эквивалентно

(5.46)

a следовательно, и

(5.47)

Вторая форма последнего выражения является обратным выражением для соотношения

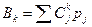, (5.48)

определяющего биноминальные моменты._г

Производящая функция для 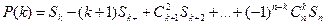на основе рассмотренного приводится к виду

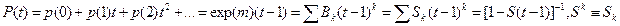
Введенные обозначения числа объектов, обладающих тем или иным из заданных свойств, не учитывали ранга или порядка этих свойств. Если учесть ранг, то можно получить решения ряда интереснейших задач теории вероятностей через производящие функции (например, вероятности достижения успеха на j-м испытании, решение задачи о встречах и т.п. [22, 23]). Но эти задачи выходят за возможности объема данной книги.

Остановимся еще на одном комбинаторном подходе к характеристике структуры конечных множеств, который, на наш взгляд, целесообразно использовать при создании систем искусственного интеллекта - нахождении представителей множеств.

Дата добавления: 2018-11-24; просмотров: 1067; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 11 121314 15 16 Следующая ⇒

Мы поможем в написании ваших работ!