Системы представителей множеств
Основной идеей комбинаторно-логических задач этого типа является задача нахождения замены системы множеств их представителями. Это, несомненно, позволит ускорить вывод в базе знаний, так как сравнения необходимо будет производить не со всем множеством объектов каждого подмножества, а только с его представителем. Постановка задач этого типа и методы их решения зависят от того, каким требованиям должны удовлетворять эти представители.
Рассмотрим две из наиболее простых задач этого типа - нахождение систем различных представителей и систем общих представителей (С.Р.П., С.О.П.). Типичным примером первой задачи является следующая. Даны пять множеств S 1= {1,2,3}, S2= { 1,2,4 }, S 3 ={1,2,5},S 4 ={3,4,5,6}, S 5 ={3,4,5,6]. Требуется выбрать такие различные числа x 1 , x 2 , x 3 , x 4 , x 5 , что  .Одним из способов выбора является x 1 =1, x 2 =2, x 3 =5, x 4 =3, x 5 =4. Но если взять множества Т1={1, 2},T2={1,2}, T 3= {1,2 },T 4={3,4,5,6}, T 5={3,4,5,6}, то такой выбор оказывается невозможным, Возникает вопрос: при каких условиях подмножества Si, i=1, 2,…,n, множества S обладают различными представителями xi ; i =1;…, n т.е.
.Одним из способов выбора является x 1 =1, x 2 =2, x 3 =5, x 4 =3, x 5 =4. Но если взять множества Т1={1, 2},T2={1,2}, T 3= {1,2 },T 4={3,4,5,6}, T 5={3,4,5,6}, то такой выбор оказывается невозможным, Возникает вопрос: при каких условиях подмножества Si, i=1, 2,…,n, множества S обладают различными представителями xi ; i =1;…, n т.е.  и
и 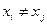 если.
если.  . Заметим, что ;не требуется, чтобы Si и Sj с
. Заметим, что ;не требуется, чтобы Si и Sj с  были различными подмножествами множества S. Ответ на этот вопрос дает теорема Ф.Холла [23,24]. Пусть, имеются n-множество S и его булеан В (S). Пусть
были различными подмножествами множества S. Ответ на этот вопрос дает теорема Ф.Холла [23,24]. Пусть, имеются n-множество S и его булеан В (S). Пусть  - некоторая m-выборка из B(S) и
- некоторая m-выборка из B(S) и  некоторая m-выборка из S.
некоторая m-выборка из S.
Подмножества S 1 , S 2 ,..., Sm имеют С.Р.П, тогда и только тогда,, когда объединение любых k из этих множеств содержит не менее k элементов. Необходимость очевидна. Достаточность этого утверждения дается следующей т е о р е м о й, задающей одновременно и нижнюю грань для числа различных представителей.
|
|
|
Пусть семейство M={S 1 , S 2,…; Sm} удовлетворяет необходимому условию существования С.Р.П., и пусть каждое из множеств S 1 , S 2 ,..., Sm состоит не менее чем из t элементов. Тогда: а) если  , то М имеет не меньше, чем t ! С.Р.П.; б) если t > m, то М имеет не менее, чем t !/( t - m )! С.Р.П. Доказательство этого утверждения методом индукции дано в [23], и мы не будем на нем останавливаться, а остановимся на практической реализации решения задачи выбора С.Р.П., так как практически очень трудно проверить, выполняются ли в данном конкретном случав условия теоремы Ф.Холла, которую можно отнести к теоремам существования. Теоремы существования чаще всего появляются там, где бывает трудно или невозможно найти алгоритм, приводящий к нахождению решения. Алгоритм, который позволяет подобрать С.Р.П. для конечного числа множеств или показать, что такой системы не существует для данного набора множеств, дал М.Холл [23, 24]
, то М имеет не меньше, чем t ! С.Р.П.; б) если t > m, то М имеет не менее, чем t !/( t - m )! С.Р.П. Доказательство этого утверждения методом индукции дано в [23], и мы не будем на нем останавливаться, а остановимся на практической реализации решения задачи выбора С.Р.П., так как практически очень трудно проверить, выполняются ли в данном конкретном случав условия теоремы Ф.Холла, которую можно отнести к теоремам существования. Теоремы существования чаще всего появляются там, где бывает трудно или невозможно найти алгоритм, приводящий к нахождению решения. Алгоритм, который позволяет подобрать С.Р.П. для конечного числа множеств или показать, что такой системы не существует для данного набора множеств, дал М.Холл [23, 24]
Рассмотрим n множеств S 1 , S 2 ,…, Sn. Найдем для них С.Р.П. или покажем, что ее найти нельзя. Произвольно выберем элемент первого множества  качестве его представителя. Поочередно будем выбирать представителей других множеств
качестве его представителя. Поочередно будем выбирать представителей других множеств  , заботясь только о том, чтобы все они были различны. Если мы доведем этот процесс до
, заботясь только о том, чтобы все они были различны. Если мы доведем этот процесс до  включительно, то получим искомую С.Р.П. Может случиться, чтo на r -м шаге мы дойдем до некоторога t-множества Sr все элементы которого b 1 , b 2 ,…, bt уже были представителями других множеств. Это, однако, еще не означает, что С.Р.П. не существует. Будем брать поочередно все те множества, представителями которых являются элементы bi ( i =1,2,…) и удалять из них все элементы последовательности b1,b2,..,bt а оставшиеся приписывать в конец этой последовательности. Так будем поступать до тех пор, пока не случится одно из двух: либо 1) мы достигнем элемента bi, который не может служить представителем, 2) последовательность исчерпывается элементами b 1 , b 2 ,…, bs как представителями множеств, В случае 2) С.Р.П. не существует. В самом деле, элементы b 1 , b 2 ,…, bs являются представителями S множеств, и по построению каждый, элемент этих S множеств содержится. в данной последовательность. Но тогда эти S множеств ,а также множество Sr образуют S+1 множеств, которое содержат только S различных элементов, что противоречит условию теорем существует С.Р.П., Ф.Холла.
включительно, то получим искомую С.Р.П. Может случиться, чтo на r -м шаге мы дойдем до некоторога t-множества Sr все элементы которого b 1 , b 2 ,…, bt уже были представителями других множеств. Это, однако, еще не означает, что С.Р.П. не существует. Будем брать поочередно все те множества, представителями которых являются элементы bi ( i =1,2,…) и удалять из них все элементы последовательности b1,b2,..,bt а оставшиеся приписывать в конец этой последовательности. Так будем поступать до тех пор, пока не случится одно из двух: либо 1) мы достигнем элемента bi, который не может служить представителем, 2) последовательность исчерпывается элементами b 1 , b 2 ,…, bs как представителями множеств, В случае 2) С.Р.П. не существует. В самом деле, элементы b 1 , b 2 ,…, bs являются представителями S множеств, и по построению каждый, элемент этих S множеств содержится. в данной последовательность. Но тогда эти S множеств ,а также множество Sr образуют S+1 множеств, которое содержат только S различных элементов, что противоречит условию теорем существует С.Р.П., Ф.Холла.
|
|
|
В случае 1) на некотором этапе мы находим элемент  ,не являющийся до сих пор представителем. Это означает, что представителем Sj 1 уже был выбран другой, элемент
,не являющийся до сих пор представителем. Это означает, что представителем Sj 1 уже был выбран другой, элемент 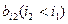 , Если i 2 > t, то значит
, Если i 2 > t, то значит  представителем которого является bi 3 ( i 3< i 2 ).Таким образом, возникает последовательность
представителем которого является bi 3 ( i 3< i 2 ).Таким образом, возникает последовательность  индексы которой убывают
индексы которой убывают  , причем в этой последовательности каждый ее член входит в множество, представителем которого является следующий член. Заменяем представителей, выбирая элементы: bi 1 для Sj 1 , bi 1 для Sj 2,… bim -1, для Sjm -1 .Элемент bim в результате этой замены освобождается для выбора в качестве представителя Sr,. Итак, S 1 ,..., Sr имеют различных представителей, и мы можем следовать тем же путем, имея в виду либо возможность дойти до Sn и получить полную С.Р.П., либо встретить случай 2) и установить не существование С.Р.П. Заключение о числе С.Р.П. получается из приведенного алгоритма как следствие.
, причем в этой последовательности каждый ее член входит в множество, представителем которого является следующий член. Заменяем представителей, выбирая элементы: bi 1 для Sj 1 , bi 1 для Sj 2,… bim -1, для Sjm -1 .Элемент bim в результате этой замены освобождается для выбора в качестве представителя Sr,. Итак, S 1 ,..., Sr имеют различных представителей, и мы можем следовать тем же путем, имея в виду либо возможность дойти до Sn и получить полную С.Р.П., либо встретить случай 2) и установить не существование С.Р.П. Заключение о числе С.Р.П. получается из приведенного алгоритма как следствие.
|
|
|
Рассмотрим решение задачи нахождения общих представителей (С.О.П.). Пусть даны два различных разбиения одного и того же множества S на К непустых составляющих:

Если существует подмножество 0 множества S состоящее из k элементов, и такое, что его пересечение с любым из составляющих не пусто  (O ∩ Ai ≠Ǿ, O ∩ Bi ≠Ǿ, i =1,2,…, k) то оно называется системой общих представителей (С.О.П.) данных разбиений. При этом каждое из пересечений оказывается состоящим только из одного элемента. Попарно взятые множества первого и второго разбиений, подобранные, если надо, соответстзующим образом, имеют один и только один общий элемент который и является их общим представителем обязательно, чтобы соблюдалось требование существования только одного общего элемента. Можно ставить условия: существование заданного числа общих элементов, заданного множества их. Критерий существования или не существования С.О.П. близок к критерию, применяемому к С.Р.П. Два разбиения множеств
(O ∩ Ai ≠Ǿ, O ∩ Bi ≠Ǿ, i =1,2,…, k) то оно называется системой общих представителей (С.О.П.) данных разбиений. При этом каждое из пересечений оказывается состоящим только из одного элемента. Попарно взятые множества первого и второго разбиений, подобранные, если надо, соответстзующим образом, имеют один и только один общий элемент который и является их общим представителем обязательно, чтобы соблюдалось требование существования только одного общего элемента. Можно ставить условия: существование заданного числа общих элементов, заданного множества их. Критерий существования или не существования С.О.П. близок к критерию, применяемому к С.Р.П. Два разбиения множеств  тогда и только тогда имеют С.О.П., когда объединение любых m из множеств Ai пересекаются не менее чем с m из множеств Bj, где m = I , ... k .
тогда и только тогда имеют С.О.П., когда объединение любых m из множеств Ai пересекаются не менее чем с m из множеств Bj, где m = I , ... k .
|
|
|
Понятие о представителях множеств и о системах представителей находит в математике многочисленные приложения: теория сетей, допустимость потоков и др. Нахождение общих представителей может быть использовано при построении доказательств с помощью нечетких множеств. Несомненно, и другие разделы комбинаторно-логических методов будут использованы при построении систем искусственного интеллекта.
Дата добавления: 2018-11-24; просмотров: 908; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
