Способы заданий отношений. Алгебра отношений.

Реляционная алгебра

В соответствии с рассмотренным ранее бинарное отношение в множестве V есть подмножество его квадрата А 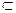V². Тогда можно дать новое определение графа как совокупности множества V с заданным в нем бинарным отношением А 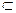V². Бинарное отношение удобно задать с помощью матрицы смежности, в которой каждый элемент (i, j) взаимно однозначно соответствует элементам множества V². Элемент, принадлежащий А 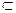V², отличается единицей, остальные элементы – нули. 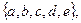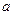Рассмотрим блок-схему ЭВМ фон Неймана (рис.3.18): V= где – устройство ввода; 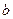– арифметическое устройство (процессор); с – устройство управления; 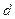– запоминающее устройство; 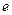– устройство вывода.

Рассмотрим информационный обмел между устройствами v_i и v_j, которые находятся в отношении А, если из устройства v_j поступает информация в устройство v_j. Это отношение может быть задано с мощью матрицы смежности следующим образом [13]:

b c d e

0 1 1 1 0

0 0 1 1 1 b

B = 1 1 0 1 1 c

0 1 1 0 1 d

0 0 1 0 0 e

Граф Д, задаваемый рассмотренным отношениям А, изображен на рис. 3.18.

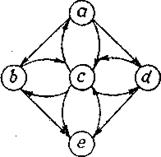
Рис. 3.18

Рассмотрим еще один способ задания бинарного отношения с помощью фактор-множества. Окрестностью единичного радиуса элемента v_i 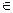V называется множество элементов v_j, таких, что (v_i, v_j)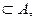 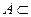V². Множество окрестностей единичное радиуса, взятых для всех элементов множества V при заданном в нем отношении 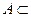V², называется фактор-множеством V/А множества V по отношению А. Фактор-множество V/А полностью определяет отношение А.

Зададим фактор-множество для рассматриваемого примера в виде двух строк, в первой из которых поместим элементы множества V, во второй – под каждым элементом запишем окрестность единичного радиуса этого элемента. Тогда вторая строка задает фактор-множества V по А:

а ъ с d е

{ b , c , d } { c , d , e } {а, Ь, d , ,е} {Ь,с,е} {с}

Одним из важных бинарных отношений является отношение упорядоченности, которое может быть определено через ранее введенные свойства графа: симетричностъ, рефлексивность и транзитивность. Бинарное отношение R в множестве V, обладающее свойствами рефлексивности 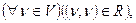антисимметричности 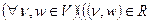и

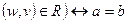
транзитивност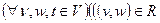и и 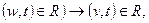называется отношением упорядоченности и обозначается ≤. Бинарное отношение в множестве V, обладающее свойствами антирефлексивности, антисимметрич-ности и транзитивности, называется отношением строгой упорядоченности и обозначается <. Отношение R в множестве V, обладающее свойствами рефлексивности и транзитивности, называется отношением предпорядка. Задавая те или иные свойства бинарных отношений и используя результаты работ [1, 8, 11, 12], можно прийти к следующей классификационной схеме свойств бинарных отношений (рис. 3.19), из которой следует, что все виды отношений разделяются на классы частичных и линейных (совершенных) отношений порядка. Отношения являются частичными, если элементы не всех пар декартова произведения являются сравнимыми с точки зрения данного отношения; они являются линейными (совершенными), если элементы любой пары декартова произведения V 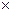V сравнимы по отношению порядка или равны.

Бинарное отношение р называется квазилинейным, или интегральным, отношением строгого порядка, если оно удовлетворяет условию антирефлексивности и следующему условию, определяющему возникновение квазилинейности:

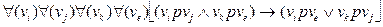
Как нетрудно показать, из последнего свойства и свойства антирефлексивности следует транзитивность (для этого достаточно положить v_k = v_j). Таким образом, рассматриваемое отношение есть отношение частичного строгого порядка, обладающее дополнительным качеством квазилейности.

Бинарное отношение называется отношением полупорядка, если оно является квазилинейным (интервальным) порядком и, кроме того, подчиняется нолутранзитивности:

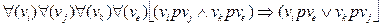
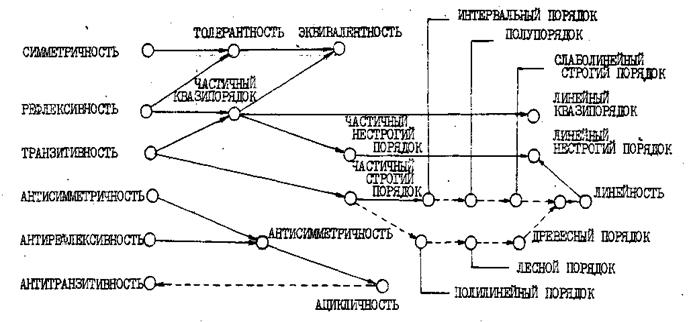
Рис. 3.19

С другой стороны, заметим, что антирефлексивное отношение при введении аксиомы полутранзитивности также приобритает свойство транзитивности и становится отношеним частичного строгого порядка, называемым полутразитивным порядком [1.13].

Таким образом, полупорядок сочетает свойства интервального и полутранзитивного порядков. Поэтому полупорядок может рассматриваться как интервальный порядок с постоянной длительностью интервала неразличимости.

Бинарное отношение р называется слаболинейным строгим порядком, если оно антирефлексивно и подчиняется аксиоме:

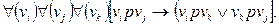
Данное отношение является полупорядком, в наибольшей степени приближающимся по своим свойствам к свойствам отношения строгого линейного порядка.

Перечисленным виды отношений находят широкое приложение при решении различных системных проблем, в особенности проблемы выбора.

На рис. 3.19 сплошными линиями со стрелками показаны пути формирования более сложных свойств отношений посредством комбинации более простых. Так, например, объединением свойства симметричности и рефлексивности приводит к толерантности, рефлексивности и транзитивности – к частичному квазипорядку, транзитивности и антирефлексивности – к частичному строгому порядку, линейности и частичного квазипорядка – линейному квазипорядку и т.д. Штриховыми линиями со стрелками показаны пути развития свойств отношений за счет их соответствующего усиления. Характерными в этом отношении является движение от ацикличности к антитранзитивности и от ацикличности к линейному строгому порядку по двум путям, первый из которых связан с постепенным переходом от квазилинейности к линейности (через интервальный порядок, полупорядок и слаболинейный порядок), а второй – с постепенным переходом от полилинейности к линейности (через полилинейный, лесной и древесный порядки).

Для бинарных отношений справедлив принцип двойственности. Отношение, обратное отношению упорядоченности, также является отношением упорядоченности. Часто принцип двойственности формулируют следующим образом: если теорема справедлива для частично упорядоченных множеств, то справедлива и двойственная ей теорема. Аналагично бинарному отношению определим n-арное отношение Т. Под n-арным отношением Т в множестве М понимается подмножество Т его n-й степени 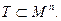Если элементы 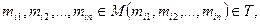то говорят, элементы 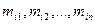находятся в отношении Т. Любое n-арное отношение может быть задано в виде списка, элементами которого являются последовательности (кортежи), определяемые этим отношением.

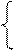Симметричным называется n-арное отношение Т в множестве М, такое, что если 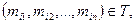то любая последовательность 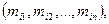получен-ная из 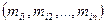перестановкой элементов, также находится в отношении Т: 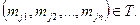В дальнейшем n-арное отношение, обладающее свойством симметричности, будем называть S-отношением, или словесным отношением. Элементы множества М, в котором определено S-отношение, будем называть буквами, а подмножества, определяемые S-отношением, - словами и обозначать греческой буквой 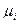с нижним индексом. Задавать S-отношение можно более удобными способами: матрицей инцидентности и модельным графом (мографом). Матрицей инцидентности 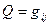называется матрица, каждому столбцу которой взаимно однозначно соответствует буква, строке – слово, определяемое S-тношением, и

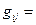0 в противном случае.

1 при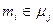

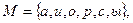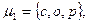
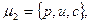
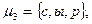
Например, S-отношение в множестве onpeделяющие слова 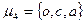с помощью матрицы инцидентности можно задать следующим образом [13]:

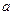u o p c ы

0 0 1 1 1 0

0 1 0 1 1 0

B = 0 0 0 1 1 1

1 0 1 0 1 0

Для задания S-отношения с помощью модельного графа каждой букве множества М ставят в соответствие вершину графа и каждой вершине приписывают идентификаторы слов, в которые эта буква входит. Процесс сопоставления каждой букве множества идентификаторов слов, в которые эта буква входит, будем называть моделизацией графа G. В результате моделизации графа G каждой вершине взаимно однозначно соответствует буква, взвешенная множеством идентификаторов слов, в которые она входит; при этом две вершины смежны, если им соответствует хотя бы один общий идентификатор. Полученную таким образом на графе функцию, областью определения которой являются вершины графа, а областью значений – множества идентификаторов слов, будем называть модельным графом (мографом) и обозначать G^м =(( V, W), E), Здесь W-монжество идентификаторов слов. На рис. 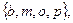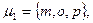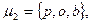З.20 задано З-отношение с помощью модального графа в множестве М= определяемое словами 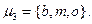Однозначно задать S-отношение с помощью графа можно, если в качества носителя графа (множество вершин) взять не только множество букв, но и множество идентификаторов слов. Такое задание S-отношение осуществляется двудольным графом. Двудольный граф, задающий З-отношение 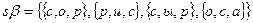в множестве 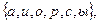изображен на рис. 3.21. Уточним теперь введенное ранее понятие модели. Моделью 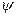называется совокупность множества М с заданными в нем отношениями:

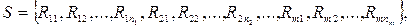
где множество М – носитель модели, а заданные отношения 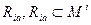образуют сигнатуру модели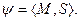

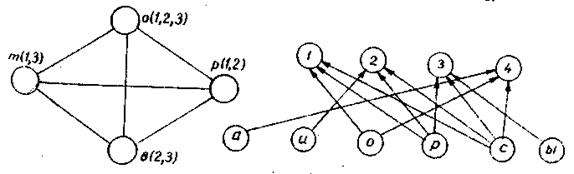
Рис. 3.20 Рис. 3.21

Степень носителя определяет арность отношения. Два отношения 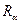и 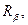имеющие одну и ту же степень, называются совместными по объединению или просто совместимыми.

Очевидно, что n-местную операцию ƒ_n (m₁, m₂,…, m_n) = m_n₊₁ можно рассматривать как (n+1)-арное отношение R_n+1, Совокупность множества с заданными в нем операциями и отношениями, следуя А. И. Мальцеву, будем называть алгебраической системой [3]. Частным случаем алгебраической системы являются алгебра отношений и ее расширение – реляционная алгебра. Рассмотрим алгебру отношений, носитель который – множество отношений, а сигнатура – операции объединений, пересечения, разности и расширенного декартова произведения отношений.

Объединением 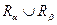двух совместимых отношени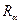й и 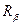является множество всех кортежей, каждый из которых принадлежит хотя бы одному из этих отношений. Объединением отношени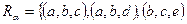й и 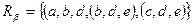является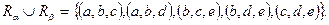

Рассмотренные отношения являются совместимыми, так как их степени равны: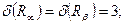

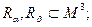
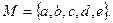
Пересечением 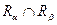R двух совместимых отношени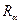й и 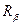является множество всех кортежей, принадлежащих как отношению 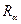так и отношению 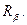Пересечением отношению 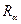и 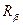является =

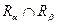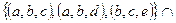
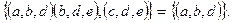
Разностью 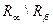двух совместимых отношени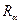й и 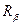является множество всех кортежей, принадлежащих отношению 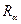и не принадлежащих отношению 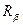. Так, например,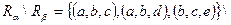

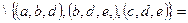
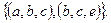
Расширенным декартовым произведением 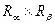двух отношени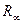й и 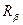является множество всех кортежей 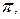таких, что 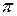- конкатенация кортежа 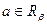и кортежа 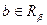(конкатенация кортеже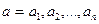й и 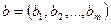, – кортеж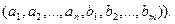

Например, для рассмотренных отношени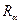й и 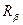расширенное декартово произведение

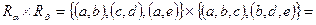
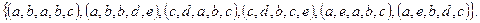
Понятия модели и алгебры отношений находят широкое применение при формализации реальных объектов. Рассмотрим, как используется алгебра отношений при создании информационного обеспечения – разработке реляционной базы данных [13] .

Основой построения реляционной базы данных является двумерная таблица, каждый столбец которой соответствует домену (или атрибуту), строка – кортежу значений атрибутов, находящихся в отношении R. Рассмотрим 5-арное отношение R₅ (экзамены) (табл. 3.2) специальности автоматизированные системы управления (АСУ) в Кишиневском политехническом институте (часть расписания). Эта таблица определяет отношение реляционной модели данных. Отношение R₅ является подмножеством декартова произведения 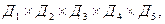в котором сомножитель является доменом Д_і. Элементами домена Д_і служат значения атрибутов. Домен Д₁ (группа) содержит значения АСУ-891 .АСУ-881, АСУ-882, АСУ-871:

Д₁ = {АСУ-891, АСУ-881, АСУ-882, АСУ-871}.

Аналогично имеем домены:

Д₂ (дисциплина):

Д₂ = {математика, физика, программирование, математические модели информационных процессов, информационная технология}.

Таблица 3.2

R₅	Д₁	Д₂	Д₃	Д₄	Д₅
1.	АСУ-891	Математика	Проф. Иванов	03.01	Ауд. 3-501
2.	АСУ-881	Физика	Проф. Петров	03.01	Ауд. 3-502
3.	АСУ-882	Программирование	Доцент Ильин	03.01	Ауд. 3-505
4.	АСУ-871	Математические модели информационных процессов	Проф. Федоров	06.01	Ауд. 3-504
5.	АСУ-891	Физика	Проф. Петров	09.01	Ауд. 3-504
6.	АСУ-881	Программирование	Доцент Ильин	09.01	Ауд. 3-501
7.	АСУ-882	Математика	Проф. Иванов	10.01	Ауд. 3-502
8.	АСУ-871	Программирование	Проф. Петров	10.01	Ауд. 3-505

Д₃ (экзаменатор):

Д₃= {проф. Иванов, проф. Петров, доцент Ильин, проф. Федоров}.

Д₄(дата проведения экзамена):

Д₄= {03.01, 06.01, 09,01, 10.01}.

Д₅(ауд.):

Д₅= {ауд. 3-501, ауд. 3-502, ауд. 3-504, ауд. 3-505}.

Порядок столбцов в таблице фиксирован, строки в общем случае могут располагаться произвольно. Цифры первого столбца 1,2, ..., 8 идентифицируют элементы отношения R₅.

Для преобразования отношений определим реляционную алгебру [13]. Носитель реляционной алгебры представляет собой множество отношений; сигнатура кроме введенных операций (объединения, пересечения, разности расширенного декартова произведения отношений) включает специальные операции над отношениями: выбор, проекцию и соединение. Операция выбора представляет собой процедуру построения горизонтального подмножества отношения, т.е. подмножества кортежей, обладающих заданным свойством. С помощью операции выбора построим отношение 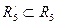(экзамены, проходящие в ауд.3-501). Результатом операции являются строки, в которых домен Д₅представлен значением ауд.3-501; это 1-я и 6-я строки. (табл.3.3).

Для определения проекции отношений множество в реляционной алгебре разбивается на два подмножества в случае бинарного отношении.

Таблица 3.3

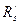
	Д₁	Д₂	Д₃	Д₄	Д₅
1	АСУ-891	Математика	Проф. Иванов	03.01	Ауд. 3-501
6	АСУ-881	Программирование	Доцент Ильин	09.01	Ауд. 3-501

и на n подмножеств – в случае n -арного отношения:

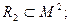
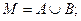
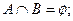
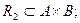
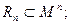
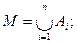
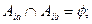
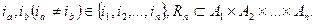
Проекцией П_р (R₂/А) бинарного отношения 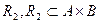на А называется множество элементов 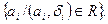. Проекцией П_р 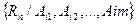n-арного отношения 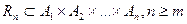на 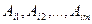называется множество кортежей 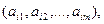где 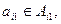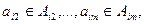каждый из которых является частью элемента n-арного отношения R_n. Проекция определяет построение вертикального подмножества отношения, т.е. множества подмножеств кортежей, получаемого выбором одних и исключением других доменов. Проекция П_р (R₅/Д₂, Д₃) порождает множество пар, каждая из которых определяет дисциплину и экзаменатора (табл.3.4). Одинаковые строки объединяются в одну. Операция соединения по двум таблицам, имеющим общий домен, позволяет построить одну таблицу, каждая строка которой образует соединение двух строк исходных таблиц.

Из заданных таблиц берут строки, содержащие одно и то же значение из общего домена; общему домену сопоставляют один столбец. Для примера рассмотрим табл. 3.5 и 3.6.

Таблица 3.4

R₂	Д₂	Д₃
	Математика Физика Программирование Математические модели информационных процессов Информационная технология	Проф. Иванов Проф. Петров Доцент Ильин Проф. Федоров Проф. Федоров

Таблица 3.5

R₅	Д₁	Д₂	Д₃	Д₄	Д₅
	АСУ-891 АСУ-881 АСУ-882 АСУ-871	Математика Физика Программирование Математические модели информационных процессов	Проф. Иванов Проф. Петров Доцент Ильин Проф. Федоров	03.01 03.01 03.01 06.01	Ауд. 3-501 Ауд. 3-502 Ауд. 3-505 Ауд. 3-504

Таблица 3.6

R₅	Д₁	Д₂	Д₃	Д₄	Д₅
	АСУ-891 АСУ-881 АСУ-882 АСУ-871	Физика Программирование Математика Информационная технология	Проф. Петров Доцент Ильин Проф. Иванов Проф. Федоров	09.01 09.01 10.01 10.01	Ауд. 3-504 Ауд. 3-501 Ауд. 3-502 Ауд. 3-505

Таблица 3.7

R_g	Д₁	Д₂	Д₃	Д₄	Д₅	Д^/₂	Д^/₃	Д^/₄	Д^/₅
	АСУ-891	Матема-тика	Проф. Иванов	03.01	Ауд. 3-501	Мате-матика	Проф. Иванов	03.01	Ауд. 3-501
	АСУ-881	Физика	Проф. Петров	03.01	Ауд. 3-502	Физика	Проф. Петров	03.01	Ауд. 3-502
	АСУ-882	Програ-ммиро вание	Доцент Ильин	03.01	Ауд. 3-505	Програ-ммиро-вание	Доцент Ильин	03.01	Ауд. 3-505
	АСУ-871	Математические модели информационных процессов	Проф. Федоров	06.01	Ауд. 3-504	Математические модели информационных процессов	Проф. Федоров	06.01	Ауд. 3-504
	АСУ-891	Матема-тика	Проф. Иванов	03.01	Ауд. 3-501	Математика	Проф. Иванов	03.01	Ауд. 3-501

Табл. 3.7 можно рассматривать как расписание экзаменов конкретной группы. Она может быть расширена, если в исходных таблицах экзаменов больше чем два.

Операцию соединения можно определить и по другим условиям (>, ≥, ≠, ‹, ≤, и т.д. ). При этом запрос в реляционной базе данных будет выполнен тем быстрее, чем меньше операций над отношениями он содержит. Поэтому к исходным рассматриваемым множествам отношений применяется стратегия преобразования, построенная на основе алгебраических законов и приводящая к минимальному выражению множеств отношений [8,13].

Таким образом, мы показали одно из применений теории графов и теории отношений при построении одного из элементов информационного обеспечения – построение реляционной базы данных. Для дальнейшего уточнения возможностей применимости теории графов рассмотрим взаимоотношение целого и части.

Дата добавления: 2018-11-24; просмотров: 488; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!