Изоморфизм графов. Связность графов

⇐ ПредыдущаяСтр 6 из 16Следующая ⇒

Ранее было отмечено, что любой граф в абстрактном смысле идентичен, или, используя более принятый термин, изоморфен некоторому геометрическому графу. Изоморфизм графов формально определяется следующим образом: графы G = (V, Е) и G^/ = (V^/, Е^/) изоморфны друг другу, если существует взаимно однозначное соотношение между V и V^/ и между Е и Е^/, сохраняющее отношения инцидентности. Если граф G, изоморфен геометрическому графу G^/, тогда G^/называется геометрической реализацией графа G.

Граф называется плоским тогда и только тогда, когда он имеет геомет-рическую реализацию в пространстве [10].

Рис.3.4 иллюстрирует очевидный, но важный факт: геометрический граф монет быть плоским, даже если его нельзя преобразовать в плоский граф с помощью непрерывной деформации. Хотя G и G^/ имеют существенные отличия с точки зрения топологии, с точки зрения теории грифов они эквивалентны.

Рис. 3.4

В качестве примеров неплоских графов приведем графы Куратовского. (рис.3.5).

K_3,3

Рис. 3.5

Для конечного графа имеет место следующее утверждение: любой конечный граф G имеет геометрическую реализацию в 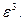На основании этого в [10] доказана теорема: граф G = (V, Е) имеет геометрическую реализацию в тогда и только тогда, когда элементам V и Е можно поставить во взаимно однозначное соответствие некоторое подмножество множества действительных чисел. Исходя из понятия кардинального числа сказанное означает, что G имеет реализацию тогда и только тогда, когда кардинальные числа множеств V и Е совпадают с кардинальными числами континуума. Идея доказательства этой теоремы состоит в том, что точки пространства 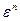можно однозначно отобразить на множество действительных чисел. Очевидно, что граф G = (V, Е) не имеет реализации в (и даже в любого положительного целого n), если нельзя установить взаимно однозначного соответствия между некоторыми множествами его вершин или ребер и подмножеством точек в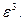

Важнейшим понятием с точки зрения практики является понятие связности [10]. Граф связен, если каждая пара различных вершин может быть соединена, по крайней мере, одной цепью. В противном случае граф называется несвязным. Определение связности графа дает следующая теорема.

Теорема [10]. Граф G = (V, Е) связен тогда и только тогда, когда множество его вершин нельзя разбить на два непустых подмножества V₁ и V₂ так, что обе граничные точки каждого ребра находятся в одном и том же подмножестве.

Доказательство этого утверждения почти очевидно. Пусть G несвязен. Выберем произвольную вершину v₁, и пусть множество V₁ состоит из вершины v₁ вместе всеми вершинами, которые могут быть соединены с v₁ цепью. Так как G несвязен, V₁ V, поэтому дополнение V₂ = V – V₁, непусто. Согласно метода построения множества V₁ни одно ребро не соединяет вершину из V₁ ни с одной вершиной из V₂, откуда и получаем разбиение, указанное в формулировке теоремы. Обратно, если такое разбиение существует, произвольно выбираем вершины v₁ V₁ и v₂ V₂. Цепь, соединяющая v₁и v₂, обязательно должна содержать, по крайней мере, одно ребро, имеющее граничные точки в обоих множествах V₁ и V₂, а так как такого ребра не существует, то граф G несвязен. Доказательство закончено.

Пусть G = (V, Е) – произвольный граф. Рассмотрим бинарное отношение р, определенное между некоторыми упорядоченными парами вершин следующим образом: vрw тогда и только тогда, когда v = w или когда существует цепь, соединяющая v с w. Очевидно оно рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Оно разбивает множество V единственным образом на классы эквивалентности взаимно связанных вершин. Для графа, изображенного на рис.3.1, такими классами эквивалентности являются 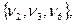. Каждый класс эквивалентности вершин вместе c ребрами из Е, инцидентными этим вершинам, образует связный подграф, называемый просто компонентой G. Легко видеть, что компонента G₁, графа G является максимальным связным подграфом в том смысле, что граф G₁не имеет связного собственного подграфа.

Граф называется деревом, если он связен и не имеет циклов. Граф, не имеющий циклов и состоящий из k компонент, называется лесом из k деревьев. Граф является деревом тогда и только тогда, когда каждая пара различных вершин соединяется одной и только одной цепью. Удаление любого ребра из дерева делает его несвязным, так как удаляемое ребро составляет единственную цепь, соединяющую его граничные точки. Если дерево Т является подграфом графа G и включает все его вершины, то говорят, что дерево Т покрывает граф G. Каждое дерево с n вершинами имеет в точности n – 1 ребро. Лес, состоящий из k деревьев, имеет в точности n – k ребер. С понятием связности тесно увязаны понятия разделяющего множества и разреза. Они возникают при изучении потоков в сетях. В этих задачах фундаментальную роль играет изучение поперечных сечений сети, отделяющих источник потока от стока, и нахождение ограничивающего поперечного сочения, которое является самим узким местом. Ясно, что узкие места определяют пропускную способность сети в целом. Пусть G = (V, Е) – связный граф F Е – подмножество множества его ребер. При этом F называется разделяющим множеством тогда и только тогда, когда подграф G^/ = (V, Е\ F) несвязен. Здесь Е\ F – разность множеств Е и F. Разделяющее множество всегда существует (если граф G имеет хотя бы две вершины), так как всегда можно положить F = Е. Примеры разделяющих множеств графа G показаны штрихом на рис. 3.6.

Рис. 3.6

Разделяющее множество разбивает граф на три компоненты, одна из которых содержит вершины множества W, обведенные кружком. Очевидно, для разбиения графа достаточно удалить только те ребра, которые соединяют множество вершин W с вершинами W'= V\W (е₁, е_2, е_3, е_4, е₅).

В общем случае, если задан связный граф G = (V, Е) и множество вершин разбито на два непустых подмножества W и W^/, множество ребер, соединяющих W с W', называется разрезом. Для любого множества W это множество ребер будет непусто в силу связности графа G,, и, следовательно, разрез определен. Для любого заданного графа совокупность разрезов, определенных различными множествами W, образует подкласс всех разделяющих множеств и, более того, любое разделяющее множество содержит, по крайней мере, один разрез в качестве своего подмножества. Особый интерес для изучения представляют минимальные разделяющие множества, т.е. такие разделяющие множества, которые не содержат собственного подмножества, разделяющего граф [10].

Минимальные разделяющие множества называются простыми разрезами. Имеют место [10, 11] следующие утверждения:

– покрывающее дерево имеет, по крайней мере, одно общее ребро с любым из разрезов графа;

– в связном графе замкнутый маршрут имеет с произвольным разрезом четное число (возможно, равное нулю) общих элементов.

С точки зрения связности интересны .два случая (рис. 3.7): наличие точки сочленения (вершины V_с , удаление которой вместе с инцидентными ей ребрами делает граф не связным) и наличие моста (удаление «моста» - одного ребра е делает граф несвязным).

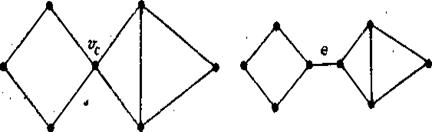
Рис. 3.7

Минимальное число вершин, удаление которых делает граф несвязным, называется вершинной связностью (G) графа. Минимальное число ребер, удаление которых делает граф несвязным, называется реберной связностью (G). Если обозначить (G) минимальную степень вершины в графе G', то имеет место следующее неравенство:

(G) (G) (G). (3.4)

Более полные характеристики связности рассмотрим после изучения матричного представления графов.

С точки зрения введенных понятий отметим ряд специальных классов графов. Граф называется обыкновенным, если он не содержит петель и параллельных ребер. Граф называется полным, если любые две
вершины являются смежными, т.е. соединяются ребром. Обычно этот термин
относится к обыкновенным графам и для каждого имеется только один полный граф (все остальные ему изоморфны). Граф называется
двудольным, если его вершины могут быть разбиты на два непересекающихся подмножества V₁ и V₂ так, что каждое ребро имеет одну граничную точку в V₁, а другую в V₂ (рис.3.8). В общем случае граф
называется k-дольным, если множество вершин можно разбить на k
непересекающихся подмножеств так, что не существует ребер, соединяющих вершины одного и того же подмножества. Граф называется k-связным, если любая пара вершин v и w соединена, по крайней мере, k цепями, которые не имеют общих вершин за исключением v и w.

Граф называется k-однородным, если (v) = k, v V. Кроме топологических свойств графов, определяющих их структуру, существует целый ряд методов приближения структуры к реальным системам. Один из

этих методов – придание свойств элементам структуры (вершинам и ребрам). Зададим одно из свойств элементам множества Е графа G = (V, Е) – направлен-ность.

Ориентированные графы

Задание направленности ребер (ориентация ребер) применительно к геометрическим графам можно интерпретировать как направление передвижения по ребру. В случае же абстрактного графа задание направленности означает, что граничные точки каждого ребра отличаются упорядочением, т.е. являются элементами декартового произведения множества вершин самого на себя.

С формальной точки зрения ориентированный граф состоит из непустого множества V, множества А, не пересекающегося с V, и отображения ∆ множества А на V V. Элементы V и А соответственно называются вершинами и дугами (или направленными ребрами), а ∆ – ориентированным отображением инциденций ориентированного графа. Если и ∆ ( ) = (v,w), то говорят, что дуга имеет начальную вершину v и конечную вершину w. Обозначение (v,w) будет употребляться для того, чтобы передать тот же самый смысл там, где ∆ не задано в явном виде. Ориентированные графы будут обозначаться через Д(V, A, ∆) или через (V, A), когда ∆ не задано в явном виде. Если ориентированный граф Д=(V, A, ∆), то соответствующим неориентированным графом для него является граф G = (V, А, Ф), для которого отображение инциденций Ф ( 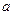) = (v & w), если ∆( ) = (v, w). Таким образом, граф G получается из графа Д отбрасыванием требования упорядоченности граничных точек каждой дуги. Структурные тормины, введенные для неориентированных графов, применимы также и к ориентированным графам. Говорят, что два ориентированных графа изоморфны, если их соответствующие неориентированные графы изоморфны в обычном смысле и, кроме того, граничные точки каждой пары соответствующих дуг упорядочены одинаковым образом.

Формально ориентированные графы Д=(V, A, ∆) и Д^/=(V^/, A^/, ∆^/) называются изоморфными, если элементы V и A могут быть поставлены во взаимно однозначное соответствие с элементами V^/ и A^/ таким образом, что ∆^/( ) = (v, w), тогда и только тогда, когда ∆( 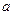) = (v, w), где и w^/ обозначают соответственно образы v и w. Таким образом, два ориентированных графа (рис.3.9,а,б) изоморфны, а граф на рис.3.9в не изоморфен им, хотя в неориентированном смысле они все изоморфны.

Рис. 3.9

С введением ориентация необходимо ввести и некоторые новые термины, описывающие локальную структуру графов [10, 12]. Если и то дуги и называются строго параллельными. Если то и не строго параллельны. Дуга считается положительно инцидентной ее конечной вершине w. Число дуг, положительно инцидентных вершине v, называется положительной степенью v и обозначается Отрицательная степень v определяется аналогично и обозначается через (Ориентированная петля, инцидентная v, считается положительно и отрицательно инцидентной с v.), Очевидно . Учитывая, что каждая дуга положительно инцидентна одной вершине и отрицательно инцидентна также одной вершине, получаем

где – число дуг графа.

Ориентированный граф называется обыкновенным, если он не имеет строго параллельных дуг и петель. Заметим, что если обыкновенный ориентированный граф имеет параллельные, но противоположно ориентированные дуги, то соответствующий неориентированный граф уже не будет обыкновенным в неориентированном смысле, так как он содержит параллельные ребра. Рассмотрим новые термины, связанные с введением направления на дугах.

Ориентированным маршрутом длины n является последовательность (не обязательно различных) дуг таких, что для соответствующей последовательности n + 1 вершин справедливо для = 1, 2, ..., n. Например, на рис.3.10 последовательность образует ориентированный маршрут длиной 4 (соответствующая последовательность вершин ).


Рис. 3.10	Рис. 3.11

Ориентированный маршрут называется замкнутым, если v₀= v_n, и незамкнутым, если v₀≠ v_n. Очевидно, незамкнутый (замкнутый) ориентирован-ный маршрут в ориентированном графе определяет соответствующий незамкнутый (замкнутый) маршрут в соответствующем неориентированном графе (обратное, вообще говоря, неверно). Например, на рис.3.10 последовательность определяет незамкнутый маршрут в неориентиро-ванном графе, соединяющий v₂и v₄, ориентированного маршрута ему соответствующего нет. Ориентированный маршрут, в котором нет повторяющихся дуг, называется путем, или контуром (ориентированным циклом), в зависимости от того, является ли он замкнутым или нет. Если все вершины различны (в этом случае дуги также различны), то путь, или контур, также называется простым. Ориентированный граф называется циклическим, если он содержит хотя бы один контур, и ациклическим в противном случае. (Заметим, что петля является специальным видом контура).

Ориентированный граф называется сильно связным, если для каждой пары различных вершин v и w существует путь из v в w и из w в v. Очевидно, что сильная связность ориентированного графа означает связность соответствую-щего неориентированного графа. Обратное, вообще говоря, неверно. На рис.3.11 граф Д, сильно связен, а граф Д₂ не является таковым, хотя в неориентированном смысле оба графа связаны.

Ориентированный граф называется сильно k-связным; если для каждой пары различных вершин существует ,по крайней мере, k путей из v в w, которые не имеют общих вершин, за исключением v и w. Для того чтобы ориентированный граф был сильно k-связен, очевидно, необходимо, но недостаточно, чтобы соответствующий неориентированный граф был k-связным в неориентированном смысле. При использовании терминов "дерево", "лес", "разделяющее множество", "разрез" и "простой разрез" без специальной оговорки считается, что направление дуг не учитывается, и рассматривается соответствующий неориентированный граф. Однако при учете направления дуг возникает несколько дополнительных понятий. Ориентированный граф является ориентированным деревом, растущим от корня v₀, если: 1) он образует дерево в неориентированном cмысле; 2) единственная цепь между v₀ и любой другой вершиной w являет путем из v₀ к w. На рис. 3.12 показано дерево (утолщенные дуги), покрывающее граф G.

Рис. 3.12

Как известно, удаление простого разреза разделяет граф точно на две компоненты. В ориентированном графе дуги разреза могут быть разделены на два множества: дуги, направленные из W к W', и дуги, направленные из W' к W (рис.3.13). Удаление первого множества разрывает все пути из W к W´, в то время как удаление последнего разрывает все пути из W' к W. Если Д сильно связен, то оба ориентирных разреза для любого разбиения {W, W'} всегда будут непустыми. С помощью ориентированных графов можно представлять бинарные отношения.

Рис. 3.13

Если р является бинарным отношением на множестве S, то граф отношения р, обозначаемый через Д_р, является ориентированным графом, вершины которого есть элементы S, такие, что существует дуга тогда и только тогда, когда spt . Обратно, если - ориентированный граф, не имеющий строго параллельных дуг, то бинарное отношение р_Д, соответствующее Д, является бинарным отношением на множестве V, таким, что тогда и только тогда когда

Таким образом, ориентированный граф является исчерпывающей формой представления, отношения, т.е. он полностью перечисляет все пары, для которых рассматриваемое отношение имеет место. Например, граф рис.3.14 является одним из возможных представлений отношений включения 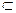, определенного на подмножествах множества, содержащего три элемента. Вершины отождествляются с соответствующими подмножествами множества В общем случае понятие ориентированного графа является более общим, чем бинарное отношение, так как позволяет использовать для отражения количественной характеристики степени связности переменное число строго параллельных дуг (в потоковых моделях – пропускную способность).

Рис. 3.14

Воспользуемся для описания специального класса ориентированных графов, не имеющих строго параллельных ребер, некоторой терминологией бинарных отношений. Рефлексивным графом (рис.3.15) называется граф, имеющий петлю в каждой вершине.


Рис. 3.15	Рис. 3.16

Симметрическим графом (рис.3.16) называется граф, в котором каждой дуге соответствует дуга

Транзитивным графом (рис.3.17) называется граф, в котором существование дуг и 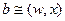означает существование дуги Из этого следует, что в транзитивном графе существование любого пути из вершины v в вершину у означает существование дуги из v в у.

Рис. 3.17

После введения бинарного отношения можно сделать дальнейшее обобщение понятия отношения, дать более строже определения ранее введенным понятиям модели и рассмотреть практическое применение алгебры отношений для построения информационного обеспечения автоматизирован-ных систем.

Дата добавления: 2018-11-24; просмотров: 632; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!