Основные понятия неориентированных графов

⇐ ПредыдущаяСтр 5 из 16Следующая ⇒

Прежде чем определить понятие графа в наиболее общей форме, рассмотрим класс графов, известных под названием геометрических графов. Это позволит с самого начала получить удобное наглядное представление различных понятий и структур, которые будут рассматриваться в дальнейшем.

Ниже будет показано, что любой граф в абстрактном смысле эквивалентен (по отношению к свойствам, изучаемым в теории графов) некоторому геометрическому графу. Таким образом, геометрический граф можно рассматривать как удобное представление любых графов, а не просто как частный пример.

Обозначим n-мерное евклидово пространство через 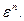Евклидово n-мерное пространство есть множество последовательностей из n действительных чисел 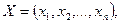в котором расстояние между любыми двумя точкам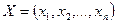и и 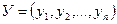определено следующим образом:

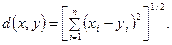(3.1)

Простой незамкнутой кривой в пространстве 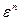называется непрерывная, самонепересекающаяся кривая, соединяющая две различные точки в 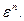Аналогично простой замкнутой кривой называется самонепересекающаяся кривая, конечные точки которой совпадают. Геометрический граф в пространс-тве 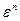есть множество 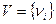точек пространства 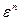и множества 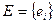простых кривых, удовлетворяющих следующим условиям:

– каждая замкнутая кривая в Е содержит только одну точку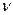
множества V;

– каждая незамкнутая кривая в Е содержит ровно две точки множества V, которые являются ее граничными точками;

– кривые в Е не имеют общих точек, за исключением точек из
тожества V .

Таким образом, геометрический граф есть просто геометрическая конфигурация или структура в пространстве 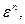состоящая из множества точек, взаимосвязанных множеством непрерывных самонепересекающихся кривых. Обычная форма представления геометрического графа показана на рис.3.1. В теории графов 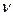и e называются геометрическими вершинами и геометрическими ребрами соответственно. Хотя многие графы, представляющие реальные объекты (после их идеализации), являются геометрическими графами, с точки зрения теории графов их единственная структурная особенность состоит в том, что с каждым геометрическим ребром связаны две (возможно совпадающие) геометрические вершины. Теория графов построена с учетом именно этой особенности и не учитывает реальной природы вершин и ребер. Таким образом, нумерация ребер и вершин, задаваемая табл.3.1,содержит вою информацию, необходимую для описания геометрического графа, изображенного на рис.3.1.

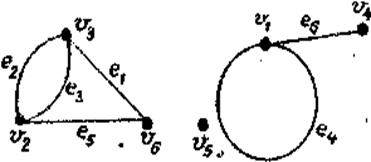
Рис. 3.1

Для общего определения графа введем понятие неупорядоченного произведения множества само на себя: S & S. В данном случае (в отличие от декартового произведения) S & t и t & S эквивалентны. Заметим, что если S имеет k элементов, то S & S состоит из 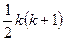различных неупорядоченных пар (в отличие от k² упорядоченных пар декартова произведения S 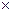S) .[10 –12].

Теперь можно дать определение неориентированного (абстрактного) графа. Граф есть совокупность непустого множества V изолированного от него множества E (возможно пустого) и отображения Ф множества E на V& V. Элементы множеств V и E называются вершинами и ребрами графа соответственно, а Ф – отображением инциденции графа. Хотя отношение инцидентности является фундаментальным в понятия графа, отображение Ф часто можно не задавать в явном виде. В таких случаях, если 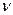и w – граничные точки ребра е, то это обозначается е ~(v & w) и читается "е соединяет вершины v & w".Будем обозначать граф через G или (V, Е, Ф), или (V, Е). Последнее обозначение используем, когда отношение инцидентности определяется неявно. Заметим, что множество Е (но не V) может быть пустым. Говорят, что граф вырожденный тогда и только тогда, когда он не имеет ребер.

Если V и Е – конечные множества (пустое множество тоже рассматривается как конечное), то G называется конечным графом. Если v = w, тогда v – единственная граничная точка е, а е называется петлей. (см. рис. 3.1, ребро е₄). Если е₁ ~ (v & w) и е₂ ~ (v & w), то е₁и е₂ называются параллельными ребрами. В частности две петли, инцидентные одной и той же вершине, являются параллельными. Говорят, что вершины v и w смежные, если существует, по крайней мере, одно ребро е, такое, что е ~(v & w). В частности, вершина v смежна сама с собой. Аналогично ребра е₁и е₂называются смежными, если они имеют, по крайней мере, одну общую граничную точку. Заметим, что смежность является отношением между двумя подобными элементами (между вершинами или между ребрами), тогда как инцидентность есть отношение между разнородными элементами.

Ребра	Вершины
е₁	v₃, v₆
е₂	v₂, v₃
е₃	v₂, v₃
е₄	v₁,
е₅	v₂, v₆
е₆	v_1, v₄
	v₅

Число ребер, инцидентных вершине v (петля учитывается дважды), называется степенью вершины v и обозначается 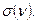Говорят, что вершина v изолирована, если 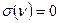(см. рис. 3.1, вершина v₅). В частности, вырожденным графом называется граф, у которого все вершины изолированы.

Учитывая, что появление каждого нового ребра добавляет по единице к степеням двух вершин (или в случае петли – два к степени одной вершины), имеем

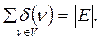(3.2)

Если V₀ и V₁ – множества вершин, имеющих четные и нечетные степени соответственно, то, очевидно, 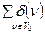четно как конечная сумма четных чисел. Отсюда следует, что

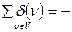
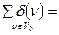
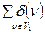(3.3)

также обязательно четно, что доказывает следующую теорему [12].

Теорема 1. В конечном графе число вершин нечетной степени четно.

Для лучшего усвоения введенной выше терминологии проиллюстрируем ее на примере графа (рис. 3.2).

Рис. 3.2

Граничными точками ребра е₁ являются вершины v₂, и v₃. Петля е₄ имеет единственную граничную точку v₁. Ребро е₂ смежно ребру е₁ и параллельно ребру е₃ (заметим, что параллельная ребра являются также и дважды смежными). Вершина v₁ смежна с v₄ и сама с собой, однако вершина v₄ не смежна сама с собой. Вершина v₅ является изолированной вершиной. Четыре вершины v₁, v₂, v₃ и v₄ имеют нечетную степень.

Множество вершин, смежных с вершиной 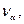называется ее окрестностью и обозначается 0 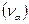или 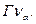Используя понятие окрестности, граф определяют как совокупность множества вершин и множества их окрестностей: G = (V, Г).

Пусть задан граф G = (V, Е, Ф). Систему G = (V₁, Е₁, Ф₁) будем называть подграфом графа G тогда и только тогда, когда выполняются следующие условия:

1) 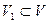и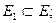

2) Ф₁(е) = Ф(е) для каждого е 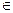Е₁;

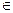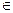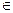3) Если е Е₁и Ф (е) = (v & w), то v V₁, w V₁.

Рассматривая геометрический граф, можно зафиксировать некоторую вершину и, последовательно двигаясь по смежным ребрам к вершинам, прийти в другую вершину или вернуться в исходную. Последовательности ребер, по которым можно двигаться непрерывным образом, играют фундаментальную роль в теории графов.

Конечная последовательность ребер графа е_1,е₂,…,е_n (не обязательно различных) называется маршрутом длиной n, если существует последовательность v₀, v₁,…,v_n из n+1 (не обязательно различных) вершин, таких что е _і ~(v_і-1& v_і) для і = 1,2,..., n. Говорят, что маршрут замкнут, если v₀=v_n, и не замкнут, если v₀ 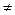v_n. В последнем случае также говорят, что маршрут соединяет вершины v₀ и v_n.

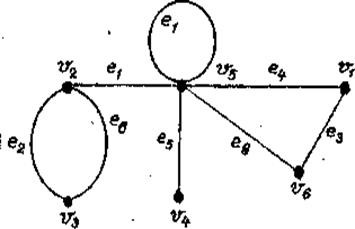
Рис. 3.3

На рис.3.3 последовательность ребер е₇, е_1, е_2, е_3, е_4, е₅образует незамкнутый маршрут, соединяющий вершины v₂ и v₄длинной 6. Ему соответствует последовательность вершин v_2, v_5, v_5, v_6, v_1, v_5,v₄. Заменяя ребро е₅ на е₇, получаем пример замкнутого маршрута длиной 6.

Если все ребра, составляющие маршрут, различны, то такой маршрут называется цепью, если он не замкнут, и циклом, если он замкнут. Если все n+1 вершин v₀, v₁,…,v_n различны (очевидно, что в этом случае ребра обязательно различны), то соответствующая цепь называется простой цепью. Если v₀ = v_n, но все остальные вершины различны, то последовательность ребер называется простым циклом [10].

Дата добавления: 2018-11-24; просмотров: 380; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!