Управляемость. Наблюдаемость. Индентфицируемость

⇐ ПредыдущаяСтр 16 из 16

После рассмотрения вспомогательных соотношений введем основные качественные характеристики динамических систем. Сделаем это более наглядно вначале на основе канонических представлений, в дальнейшем рассмотрим вопросы управляемости, наблюдаемости и индентифицируемости на основе более общих системных принципов.

Управляемость. Система управляема, если она может быть переведена из любого состояния q(t₀) при t = t₀ в любое другое желаемое состояние q(t) за конечный интервал времени 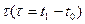путем приложения кусочно-непрерывного входного воздействия и(t), 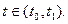. Все критерии анализа управляемости основаны на рассмотрении канонического уравнения состояния и на полиномиальном разложении 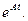В соответствии с критерием Гильберта система, заданная в канонической форме

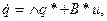(6.37)

управляема, если ни одна из строк матрицы В* не является нулевой (т.е. для управляемости в каждой строке должен быть по меньшей мере один, ненулевой элемент В*).

Рассмотрим случай, когда одна или более строк матрицы В* нулевые, то система неуправляема. Для этого перепишем уравнение (6.35) в скалярной форме:

…………………

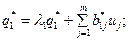
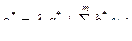
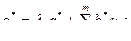(6.38)

Поскольку взаимодействие между каноническими переменными состояния отсутствует, становится очевидным, что если в любой i-й строке уравнения (6.38) 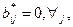то на соответствующую переменную состояния q _i*; не может повлиять выбор управления. Следовательно, это состояние системы неуправляемо. Пример на управляемость:

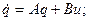
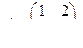
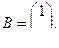
В соответствии с ранее рассмотренным примером матрица преобразования для диагонализации А задается соотношением

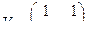
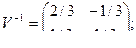
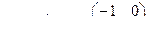
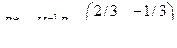
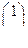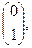
что дает каноническую систему уравнений:

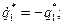
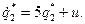
Так как на состояние 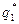не влияет входной сигнал управления, то система, очевидно, неуправляема.

Наблюдаемость. Понятие наблюдаемости дополняет понятие управляемости. Если управляемость требует, чтобы каждое состояние системы было чуствительно к воздействию входного сигнала, то наблюдаемость требует, чтобы каждое состояние системы влияло на измеряемый выходной сигнал.

Система наблюдаема, если все ее состояния можно непосредственно или косвенно определить по выходному вектору системы. Поэтому, когда определенное состояние (или изменение этого состояния) не влияет на выходной вектор, система ненаблюдаема. Ненаблюдаемая система не может быть идентифицирована. Критерий наблюдаемости Гильберта рассмотрим на примере системы уровнений после канонизации:

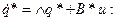(6.39)

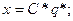
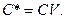(6.40)

Система наблюдаема, если ни один из столбцов С* не является нулевым. Если, по крайней мере, один столбец С* нулевой, то система становится ненаблюдаемой.

Пример. Рассмотрим систему

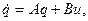
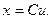
где

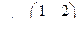
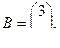
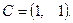
Из предыдущего примера найдем

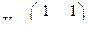
Для определение наблюдения системы вычеслим

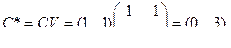
Поскольку первый столбец матрицы С* равен нулю, система ненаблюдаема.

Дадим более общее понятие управляемости, наблюдаемости и введем понятие идентифицируемости [29, 30]. Пусть объект описывается следующими уравнениями (в дискретной форме):

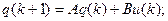(6.41)

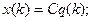(6.42)

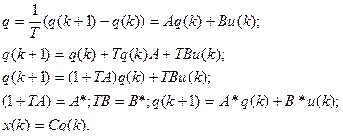
В дальнейшем значки * при А и В будем опускать. Здесь q – вектор размерности n . Объект называется управляемым, если можно найти такой (может быть неограниченный) вектор управления, который из произвольного начального состояния переводит систему в произвольное конечное состояние за ограниченное время. Таким образом, необходимо найти условие, при котором можно определить управление, которое переводит систему из состояния q(0) в заданное состояние q(n):

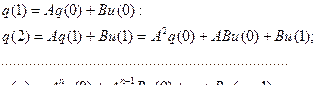(6.43)

или

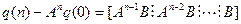
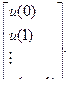(6.44)

Поскольку 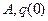и и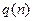звестны, левая часть последнего уравнения определена. Единственное решение и существует только тогда, когда матрица 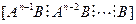имеет ранг 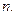В этом случае (А, В) называют управляемой парой.

Объект называется наблюдаемым, если по измерениям выходного сигнала объекта можно определить его состояния. Таким образом, необходимо найти условие, при котором по измерениям можно определить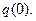

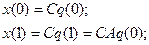
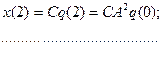(6.45)

или, транспонируя, имеем

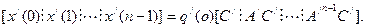(6.46)

Так как векторы х известны, единственное решение q(0) существуеттолько тогда, когда матрица 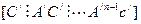имеет ранг n. В этом случае (АС) называется наблюдаемой парой.

Объек называетс идентифицируемым, если по измерения координат состояния, объекта можно опередлить матрицу системы А:

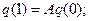
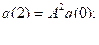(6.47)

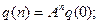
или

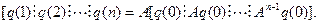(6.48)

така как векторы q известны, единственное решение для А существует только тогда, когда матрица 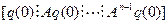имеет ранг n.

Для иллюстрации этих понятий выберем простую систему второго порядка 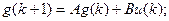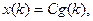где

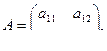
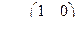
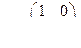
Рассмотрим управляемость системы. Имеем

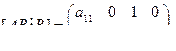
Система управляема, если ранг равен 2, т.е. когда 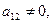и не наблюдаема, если 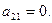. Видно, что, когда 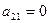отсутствует управление координатной 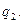Отметим, что все остальные параметры 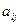могут равняться нулю, но система останется управляемой.

Перейдем к наблюдаемости. Имеем

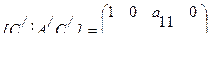
Система наблюдаема, если ранг равен 2, т.е. когда 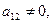и ненаблюдаема, когда 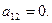В этом случае выходная координата х не содержит информации о 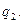Снова отметим, что все остальные параметры могут равняться нулю, но система останется наблюдаемой.

Идентифицируемость:

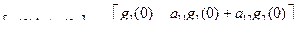
Система идентифицируема, если ранг матрицы равен 2, и неидентифицируема, если определитель матрицы равен нулю. Для этого оба столбца матрицы должны быть линейно зависимы. Различают простейший случай, когда 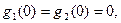т.е. объект, который находится в состоянии покоя, не может быть идентифицирован, и нетривиальный случай, когда

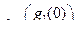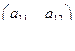
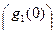
или

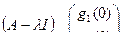= 0.

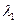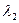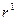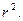В этом случае нужно найти собственные значения и и соответствующие собственные векторы и Если 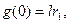,то возбуждается только одна гармоника объекта 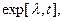а гармоника 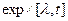не идентифицируется. Если 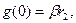то может быть идентифицирована одна только гармоника 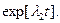Таким образом, объект идентифицируем только тогда, когда начальное условие g(0) возбуждает все гармоники объекта.

В современной теории автоматического управления информация о состоянии служит для оптимизации алгоритмов управления характеристик всей системы. Кроме того, в функцию качества входят внутренние параметры процесса или на них накладываются ограничения. Поэтому преимущество имеет выбор в качестве переменных состояния измеряемых параметров.

Всякая возможность независимого накопления энергии в системах увеличивает ее порядок на единицу и обусловливает введение переменных состояния. В электрических и механических системах токи, протекающие через индуктивности, приводят к накоплению магнитной энергии, напряжения на емкостях – к накоплению электрической энергии,скорости движения или соответственно вращения подвижных масс приводят к кинетической энергии, а растяжение пружин или перемещение масс (в направлении против земного притяжении) – к потенциальной энергии. Очень часто оказывается целесообраз-ным брать эти измеряемые параметры в качестве переменных состояния. Для выяснения свойств матрицы переходов рассмотрим решение векторного дифференциального уравнения.

Для однородного уравнения состояния

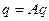(6.49)

аналогично скалярному случаю делаем подстановку:

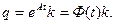(6.50)

Матричная экспоненциальная функция Ф (t) представляется в виде следующего ряда:

(6.51)

Можно показать, что Ф(t) для любого конечного значения и любой квадратичной матрицы A и имеет равномерную сходимость. Вследствие этого суммирование и дифференцирование могут проводиться независимо друг от друга, и можно записать

(6.52)

Можно показать, что выражение (6.50) обращает в тождество однородное уравнение.

Решение неоднородного уравнения

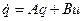(6.53)

состояния рассмотрим с помощью метода, в котором постоянные k являются переменными (метод вариации произвольных постоянных), и подставим (6.50) в неоднородное уравнение (6.53):

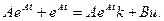(6.54)

отсюда

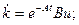(6.55)

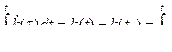
Подстановка в (6.50) дает

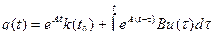(6.56)

при t = t₀ , получаем

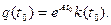(6.57)

Из (6.56) можно исключить постоянную k(t₀):

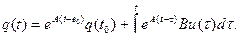(6.58)

обычно можно положить t = 0:

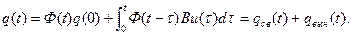
Это есть уравнение переходного процесса системы. Первое слагаемое 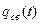определяет свободную составляющую системы, зависящую от начального состояния q(t₀), а второе слагаемое q_вын(t) – вынужденную составляющую, вызванную входным сигналом u(t) в интервале [t₀, t].

Матричная экспоненциальная функция, представленная в виде выражения (6.52):

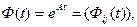(6.59)

называется матрицей перехода, или фундаментальной матрицей. Ее значение станет ясно, когда мы подробнее рассмотрим уравнение переходного процесса невозмущенной системы:

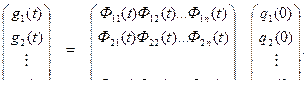(6.60)

Очевидно, элемент 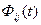этой матрицы перехода описывает процесс перехода і-й переменной состояния, когда j-я переменная имеет начальное состояние I, а все остальные начальные значения являются нулями. В целом матрица перехода описывает переход невозмущенной системы из одного начального состояния в другое [30].

Целый ряд важных свойств матрицы перехода Ф(t) получим исходя из существования и однозначности решения однородного уравнения (6.49), которое является уравнением невозмущенного движения:

1) 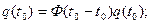(6.61)

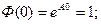(6.62)

2) если система переводится из состояния 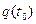сначала в состояние 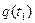и затем в состояние 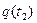и это сравнивается с прямым переводом ее в состояние :

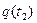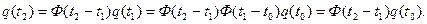(6.63)

то находят

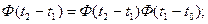(6.64)

3) так как матрица перехода, как показывает ее разложение в ряд, является не особой, то левую часть уравнения (6.64) можно умножить на обратную матрицу:

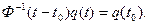(6.65)

В противоположность этому можно записать

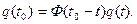(6.66)

Сравнивая выражения, получаем

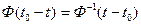(6.67)

или

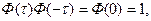(6.68)

и отсюда, как и в уравнении (6.67),

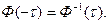(6.69)

Преобразование состояния, осуществленное с помощью матрицы nepeхода, может быть применено также и в случае противоположного отсчета времени.

При рассмотрении вопроса об идентифицируемости систем мы получили критерий, который показывает, что, чтобы определить матрицу системы А, необходимо выполнить условие, в которое также входит матрица системы.

Учитывая соотношение 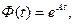вначале определяют матрицу переходов (или фундаментальную матрицу 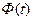), что эквивалентно решению задачи идентификации. Для нахождения матрицы перехода 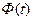часто используют интегрирование однородного дифференциального уравнения. Постоянные интегрирования определяются из начальных условий, результаты подставляются в уравнения невозмущенного переходного процесса 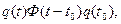откуда может быть найдена 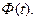Целесообразнее, особенно при определенных предположениях [26], оказываются следующие пути.

Законченное решение позволяет получить формула интерполяции Лагранжа – Сильвестра. Она применима к матричным функциям, которые могут быть представлены в виде сходящихся степенных рядов 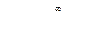где матрица А с n отличающимися друг от друга собственными значениями 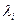соответствует формуле интерполяции Лагранжа для аппроксимации функций с помощью многочленов. Матрица перехода 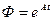представляет собой такой степенной ряд. Формула Сильвестра гласит:

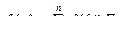(6.70)

где

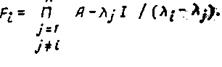(6.71)

Применив ее к расчету матрицы переходов, получим

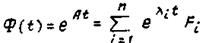(6.72)

Применение преобразования Лапласа к однородному дифференциальному уравнению 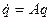позволяет получить формулу, очень похожую на формулу Сильвестра, которую можно использовать не только для случаев с простыми корнями.

С помощью преобразования подобия матрица с n совершенно различными корнями 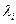может быть приведена к диагональной матрице 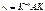; решение относительно и дает 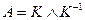. Здесь К является матрицей собственных векторов. В качестве к можно взять матрицу Вандерманда, а 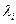- из опытных кривых [30]. Для двух подобных матриц А и 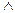, соответствующих уравнению 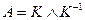, справедливо 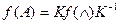. Отсюда можно найти 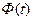из выражения 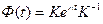, причем, если известны корни 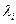, сразу можно записать матрицу :

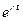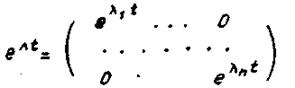(6.73)

Рассмотренные способы дают решение в аналитическом виде и требуют больших затрат времени на определение собственных значений матрицы А, т.е. корней характеристического уравнения системы. При расчете матрицы перехода с помощью формулы Тейлора

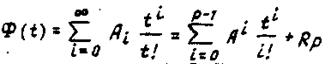
в системах с сосредоточенными параметрами для отдельных элементов матриц получим полиномы в функции t, которые могут быть записаны в виде сумм показательных функций е.Определить эти суммы очень трудно. Поэтому этот путь практически приемлем с использованием ЭВМ. Если елементи матрицы перехода 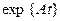должны быть определены с относительной ошибкой 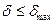, то требуемое число членов формулы Тейлора может быть найдено с помощью критерия

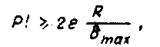(6.74)

где е - натуральное число и 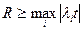является оценкой наибольшего собственного значения матрицы 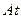. Многочисленные практические примеры на определение переходной матрицы приведены в [26, 30].

ЛИТЕРАТУРА

1. Калинин В.Н., Резников Б.А. Теория систем и управления. Л.: изд. ВИКИ им. А.Ф.Можайского, 1978.

2. Бурбаки Н. Теория множеств. М.: Мир, 1965.

3. Мальцев А.И. Алгебраические системы. М.: Наука, 1970.

4. Садовский В.А, Основания общей теории систем. М.: Наука, 1974.

5. Кемени Д., Снелл Д. Конечные цепи Маркова. М.: Наука, 1970.

6. Кон П. Универсальная алгебра. М.: Мир, 1967.

7. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970.

8. Шрейдер Ю.А. Равенство, сходство, порядок. М.: Наука, 1971.

9. Гильберт Д., Бернайс П. Основания математики. М.: Наука, 1979.

10. Басакер Р., Саати Т. Конечные графы и сети. М.: Наука, 1974.

11. Харари Ф. Теория графов. М.: Наука, 1973.

12. Берж К. Теория графов и ее применение. М.: ИЛ, 1962.

13. Горбатов В.А. Основы дискретной математики. М.: Высшая школа, 1986.

14. Коршунов Ю.М. Математические основы кибернетики. М.:Энергоатомиздат, 1987.

15. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука, 1984.

16. Поспелов Д.А. Логические метода анализа и синтеза схем.М.;Л.: Энергия, 1964.

17. Новиков П.С. Элементы математической логики. М.: Физматгиз, 1959.

18. Рубашкин В.М. Представление и анализ смысла в интеллектуальных информационных системах. М.: Наука, 1989.

19. Грэй П. Логика, алгебра и базы данных. М.: Машиностроение,1989.

20. Интеллектуализация ЭВМ/Е.С.Кузин, А.И.Ройтман, И.Б.Фоминых, Г.К.Хахалин. М.: Высшая школа, 1989.

21. Вагин В.Н. Дедукция и обобщение в системах принятия решений.М.: Наука, 1988.

22. Риордан Дж. Введение в комбинаторный анализ. М.: ИЛ, 1963.

23. Рыбников К.А. Введение в комбинаторный анализ. М.: Изд-во Московского университета, 1985.

24. Холл М. Комбинаторика. М.: Мир, 1970.

25. Комбинаторный анализ. Задачи и упражнения/Под ред.К.А.Рыбникова. М.: Наука,1982.

26. Директор С., Рорер Р. Введение в теорию систем. М.:Мир,1974.

27. Гроп Д. Методы идентификации систем. М.: Мир, 1979.

28. Сингх М., Титли А. Системы: декомпозиция, оптимизация и управление. М.: Машиностроение, 1986.

29. Эйкхофф П. Основы идентификации систем управления.М.:Мир,1975.

30. Райнике Р. Кибернетические основы и описание непрерывных систем. М.: Энергия, 1978.

СОДЕРЖАНИЕ


Введение…………………………………………………………………….	3
1. Основные системные понятия………………………………….	4
1.1. Определение системы. Модели. Классификация систем. Структура и свойства системы……………………………………………………	4
1.2. Понятие управления. Принципы управления………………………..	6
2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ……………………………………...	9
2.1 Варианты построения основной математической общей теории систем…………………………………………………………………..	9
2.2. Множества. Основные определения. Операции над множествами...	9
3. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ…………………………………………..	16
3.1. Основные понятия неориентированных графов……………………..	16
3.2. Изоморфизм графов. Связность графов……………………………...	20
3.3. Ориентированные графы……………………………………………...	25
3.4. Способы задания отношений. Алгебра отношений. Реляционная алгебра………………………………………………………………….	29
3.5. Разбиения и расстояния на графах……………………………………	38
3.6. Операции над графами………………………………………………..	57
4. МАТЕМАТИЧЕСКАЯ ЛОГИКА. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ И ПРЕДИКАТОВ…………………………………………………………...	58
4.1. Функции алгебры логики и их основные свойства………………….	58
4.2. Классы ФАЛ. Теорема Поста–Яблонского………………………….	63
4.3. Синтез логических схем……………………………………………….	66
4.4. Логические исчисления………………………………………………..	79
4.5. Модели представления знаний………………………………………..	92
4.6. Логический вывод решений с помощью исчисления предикатов…	100
5. КОМБИНАТОРНЫЙ АНАЛИЗ……………………………………………	112
5.1. Выборки. Сочетания. Перестановки. Распределения………………..	112
5.2. Производящие функции для сочетаний и перестановок……………	116
5.3. Метод включения и исключения……………………………………..	122
5.4. Системы представителей множеств………………………………….	125
6. ГОСТРОЕНИЕ ЮДШІЕЙ СИСТЕМ НА ОСНОВЕ МЕТОДА ПРОСТРАНСТВА СОСТОЯНИЙ…………………………………………	128
6.1. Состояния и движение динамической системы……………………..	128
6.2. Управляемость. Наблюдаемость. Идентифицируемость……………	137
Литература………………………………………………………………….	146

Дата добавления: 2018-11-24; просмотров: 407; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 11 12 13 14 1516

Мы поможем в написании ваших работ!