Выборки. Сочетания. Перестановки. Распределения.

⇐ ПредыдущаяСтр 12 из 16Следующая ⇒

С понятием выборки связывают как саму операцию выделения подмножества заданного множества, так и ее результат – выбранное подмножество. Рассмотрим множество A мощности n. Из него возьмем r- выборку где . Число r называется объемом выборки. Если в r-выборке учитывается порядок следования элементов, то r-выборка называется r-перестановкой, если не учитывается - r-сочетанием. Например, две 5-выборки из множества и представляют собой равные 5-сочетания и в то же время различные 5-пeрестановки. Неоднозначность решения комбинаторных задач породила задачу определения количества комбинаторных расположений. Задача подсчета числа r-выборок из n-множеств исторически была одной из первых задач комбинаторики. Найдем число всех возможных n-перестановок из n-множества. Обозначим искомое число через . Задача сводится к последовательному применению правила произведения. Действительно, в n-множестве имеются n возможностей для выбора первого элемента r перестановки. Как только такой выбор сделан, остается (n -1) возможность для выбора второго, затем (n-2) возможности для выбора третьего элемента и т.д.; для выбора r-го элемента будет n - r +1 возможность по правилу произведения .Откуда следует . Примем 0!= I. При выборке с возвращением, очевидно, .Подсчитаем теперь число сочетаний, обозначая его . Начнем со случая, когда все элементы в r-сочетании различны. Легко видеть, что r-сочетаний из n-множеств в r ! раз меньше, чем число r-перестановок из элементов того же множества. Следовательно,

Рассмотрим случай, когда элементы в r-сочетании могут повторяться. Подсчитаем число r-сочетаний c повторениями из n-множества S. Пусть элементы множества S занумерованы числами 1, 2,,.,. Тогда вместо r -выборок из множества S мы можем рассматривать соответствующие им (взаимно однозначно) r-выборки из множества S ' =1, 2,... . Всякая r-выборка из S ' может быть записана в виде , где (равенство номеров отвечает случаю одинаковых элементов в соответствующей r выборке из S). r-выборке A (элементы в ней не обязательно различны) поставим в соответствие r – множества ,в котором элементы различны. При этом r-множества A ' являются r-сочетаниями без повторений из (n+r-1) множества {1,2…, n , n +1,…, n + r -1}, число которых равно по ранее доказанному . Этот результат можно получить также из следующих рассуждений. К r-сочетаниям с повторениями из n-множества S (например, к 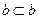из S ={a , b , c , d , e} припишем все n элементов множества S, и полученные n + r элементов запишем по порядку, помещая одинаковые элементы рядом: ( abbbccde ), затем подмножества одинаковых элементов разделим n -1 черточками . Наконец, заменим все элементы между черточками на точки. Таким образом, мы сопоставляем r -сочетанию расстановку n -1 черточек в n + r -1 промежутках между n + r точками. Что можно сделать способами. Одним из важных комбинаторных объектов, связанных с "упорядочением" и "беспорядком", являются подстановки.

Например, ряд чисел Р = (4, 3, 7, 5, 6, 9, 2, 8, I, 12, II, 10) можно рассматривать как нарушение порядка первых двенадцати чисел натурального ряда. Его можно записать в виде подстановки (в первой строке - естественный порядок, во второй - нарушенный):

I, 2 3 4 5 6 7 8 9 10 II 12 (5.2)

4 3 7 5 6 9 2 8 1 12 II 10

Эта запись показывает, что при перестановке Р элемент I перешел в 4, 2 - в 3, 3-в7 и т.д. Перестановка Р может быть записана иначе: Р = (I, 4, 5, 6, 9) (2, 3, 7) (10, 12) (8)(11), где каждая скобка есть перестановка, действующая только на элементы, заключенные в данной скобке, и не затрагивающая элементы, не заключенные в ней. Представление перестановки в таком виде называется разложением ее на циклы. Это разложение единственно с точностью до циклических перестановок элементов внутри циклов. Например, (2, 3, 7), (3, 7, 2), (7, 2, 3) есть различные записи одного и того же цикла.

Пусть некоторая перестановка содержит К₁ циклов, состоящих из одного элемента, т.е. 1-циклов, К₂- 2 циклов,K₃ - 3циклов и т.д. Тогда она называется перестановкой.

Очевидно, что . Число перестановок вида определяется формулой [22]:

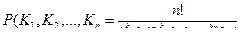(5.3)

которая получается из следующих рассуждений. Рассмотрим k ₁ скобок для записи циклов длиной 1, затем K₂ скобок для записи циклов длиной k ₂ и т.д. На имеющихся внутри всех скобок n позициях можно расставить n элементов n ! способами, и всякий раз мы получим запись перестановки вида (k ₁ , k ₂ ,.... k_n). Однако среди этих n ! записей встречаются различные записи одной и той же перестановки. Выясним, сколько различных записей имеет одна перестановка. Во-первых, каждый цикл в пределах данной скобки можно записать i способами. Во-вторых, k_i !способами можно переставить скобки, где записаны циклы длиной i. По правилу произведения получаем, что семейство циклов длиной і может быть представлено i^k_ik_i ! способами. Заставляя пробегать значения от I до n и снова применяя правило произведения, получаем, что существует N =1 ^k ¹ k ₁ !2 ^k ² k ₂ !... . n^kn k_n ! способов записи каждой перестановки вида (k₁,k₂,…,k_n). Следовательно, всего имеется n !/ N таких перестановок. Представление перестановок в виде произведения циклов служит источником многих комбинаторных задач, например: найти число перестановок n-множества, имеющих заданное число циклов (без учета длины циклов); оставляющих заданные элементы неподвижными; имеющих данное число циклов заданной длины и т. д.

Во многих задачах некоторая совокупность элементов распределяется по некоторому множеству ячеек. Задачи этого класса существуют с давних пор и имеют разработанную методику решения. Эти задачи появляются в самых различных постановках: разбиениях множеств, рассечении графов, сетей, группировках станков, организации работы автоматизированных складов, описаниях предметных областей в системах искусственного интеллекта. В теоретическом плане они интерпретируются как отображение одного множества (элементов) на другое множество (ячеек) [22, 25].

Сложившиеся способы решения задач этого класса зависят от условий, накладываемых на виды распределяемых элементов, способы распределения, виды и. вместимость ячеек. Для подсчета числа распределений необходимо уточнить, являются ли элементы данного множества и ячейки различимыми (например, занумерованы) или нет. В соответствии с этим задачи делятся на следующие четыре класса:

(A)элементы множества различимы, ячейки также различимы;

(B)элементы множества неразличимы, ячейки различимы;

(C)элементы множества различимы, ячейки неразличимы;

(Д) как элементы множества, так и ячейки неразличимы между собой Внутри каждого из этих классов задачи в свою очередь различаются видом отображений, задаваемых конкретными условиями. Например, задачи класса (А): образование слов длиной r из алфавита, состоящего из n букв. К классу (А) относятся, в частности, следующие случаи различимости элементов и ячеек:

(AI) множество N имеет (k ₁ , k ₂ ,.... k_m)-спецификацию, если оно имеет k ₁ элементов первого вида (например, цвета), k ₂ элементов второго вида, К _m элементов m-го вида,(при этом k ₁ ,+ k ₂ +…+ k_m = n);

(А2) r-множество ячеек R имеет (n ₁ , n ₂ ,…, n_r)-специфика-
цию , если в i-й ячейке помещаются n_i элементов i =1,2,…,r ;

(АЗ) элементы в ячейках упорядочены, т.е. две ячейки считаются заполненными по-разному, если различно упорядочение помещенных в них (даже одних и тех же) элементов; ограничение на объем ячеек не накладывается.

Рассмотрим пример. Пусть множество N имеет (р, g)-спецификацию, т.е. содержит р элементов первого вида и g элементов второго вида; p + g = n. Требуется найти, сколько существует распределений элементов множества N по r различным ячейкам без ограничений на число элементов в каждой из ячеек. Элементы первого вида могут быть размещены по r ячейкам 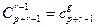способами, а элементы второго вида способами. Общее число распределений согласно правилу произведений . Если имеет место (k ₁ , k ₂ ,.. ., k_m) - спецификация множества N , то число распределений n элементов по его r различным ячейкам равно

(5.4)

В задачах класса (В) множество элементов N неразличимо, а множество R различимо. Рассмотрим два важных случая,

I. Элементы N размещаются по ячейкам множества R так, что ни одна ячейка не пуста (на рис.5.1 показано распределение п =10 элементов по h = 4 ячейкам). Как видно, задача сводится к определению числа способов провести r-1 линий в n-1 промежутках между элементами; это число равно

Рис. 5.1

2. Элементы из N размещаются по ячейкам из R так, что могут быть пустые ячейки. Метод решения задач этого типа в основном тот же. К множеству N присоединяется r символических "пустых элементов". При этом задача сводится к определению числа способов провести r-1 .линий в n + r -1 промежутках между элементами. Это число равно . К задачам данного типа относится, например, следующая: найти число решений уравнения x ₁ + x ₂ +...+х _r = n в неотрицательных целых x_i: i = 1, 2, ,.., r.

Оставшиеся два типа задач (С) и (Д), в которых неразличимыми оказываются ячейки для заполнения, представляют при попытках их решения значительные трудности. Их обычно называют объединенным именем неупорядоченных разбиений. Задачи типа (С), где неразличимы только ячейки, а распределяемые элементы различимы, поддаются в отдельных случаях решению. Приведем некоторые результаты [22].

Если учитывается порядок попадания элементов в ячейки и пустые ячейки не допускаются, то искомое число распределений равно [22]:

(5.5)

В случае, когда допускается 1, 2,…, r пустых ячеек, то искомое число распределено

(5.6)

При снятии требования о порядке заполнения ячеек элементы число распределений определяется по формуле

(5.7)

Число S ( n , r ) называют числом Стирлинга 2-го рода. Если допускается пустые ячейки, а порядок заполнения не учитывается, то число распределений

(5.8)

Задачи типа (Д), когда множества N и R состоят из неразличимых
элементов, оказались наиболее трудными и теория их решения еще далеко не разработана. Наиболее известной интерпретацией данного случая является теоретико-числовая задача о разбиении натуральных чисел на натуральные слагаемые.

Дата добавления: 2018-11-24; просмотров: 679; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!