Метод прямого пассивного поиска.
Если все точки X0, X1, X2,...,XN назначаются заранее (до проведения испытаний), то метод поиска называется пассивным методом поиска
Метод золотого сечения.
Метод золотого сечения (метод Фибоначчи)— метод поиска экстремума действительной функции одной переменной на заданном отрезке. В основе метода лежит принцип деления отрезка в пропорциях золотого сечения (соотношение двух величин a и b, a < b, когда справедливо a/b = b/(a+b)).
Критерий окончания счета. Обусловленность вычисления минимума функции.
Критерием окончания решения является равенство с заданной степенью точности концентраций по всем компонентам и для всех ступеней, полученных на двух последующих итерациях. [
Методы многомерной оптимизации. Задача безусловной минимизации функций многих переменных.
Все методы многомерной оптимизации делятся на два класса: 1) Градиентные 2) Безградиентные
Градиентные методы — численные методы решения с помощью градиента задач, сводящихся к нахождению экстремумов функции.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Понятие о методах спуска. Покоординатный спуск. Метод прямого поиска.
Вход: функция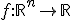 
Выход: найденная точка оптимума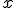 
1. Инициализация некоторым значением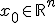 
2. повторять:
§ для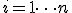 
Критерий остановки
|
|
|
1. 
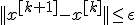
2. 
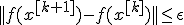
Здесь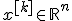 
- значение, полученное после 
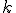-го шага оптимизации. 
- наперед заданное положительное число.
Метод прямого поиска для решения задач оптимизации это такой метод, в котором не используется ни какая информация о градиенте целевой функции. В противоположность обычным традиционным методам поиска точки минимума, в которых для поиска самой точки минимум используется информация о градиенте целевой функции или о производных различного порядка, в алгоритме метода прямого поиска анализируется определенный набор точек вокруг текущей точки. Причем ищется такая точка, в которой значение целевой функции меньше, чем значение в текущей точке. Методы прямого поиска для решения задач оптимизации можно использовать тогда, когда отсутствует какая-либо информация о дифференцируемости целевой функции или для случая прерывистой функции.
Дата добавления: 2018-11-24; просмотров: 491; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!