Явные и неявные численные методы решения систем ОДУ. Их особенности.

Найти решение ОДУ первого порядка 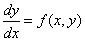на отрезке при условии

При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 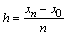, расчетными узлами служат точки промежутка [x₀, x_n].

Интегрируя уравнение на отрезке , получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

то получим явную формулу Эйлера:

, .

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

Геометрическая интерпретация метода Эйлера:

Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной , можно записать уравнение касательной к графику искомой функции в точке :. при этом если использовать формулу правых прямоугольников: , то придем к методу

, .

Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Методы Эйлера: простой, модифицированный и усовершенствованный. Метод Рунге-Кутты. Многошаговый метод Адамса.

метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

где y_i+1 это искомое значение функции в точке x_i+1.

Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить y_i+1 , если известно y_i в точке х_i:

в методе Эйлера используется простейшая формула интегрирования - формула прямоугольников по левому краю отрезка.

модифицированный. Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

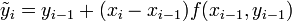Коррекция:

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты.

Усовершенствованный метод Эйлера. (метод Эйлера второго порядка). В этом методе для вычисления функции y(x) в одной точке требуется дважды вычислить функцию f (x, y):

y_i+1 = y_i+ hf (x_i+ h/2, y_i+ hf (x_i, y_i)).

Погрешность этого метода пропорциональна h²,т.е. |y_i-y_i*| < O (h²).

Методы Рунге-Кутты

В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [x_i+1 x_i]

тогда можно переписать так:

Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции y_i+h/2 и y_i+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений

Алгоритм Рунге-Кутты третьего порядка - РК3 (погрешность порядка h³):

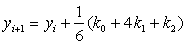(6.8)

где

Алгоритм Рунге-Кутты четвертого порядка- РК4 (погрешность порядка h⁴):

(6.9)

где

Алгоритмы третьего и четвертого порядков требуют на каждом шаге трех и четырех вычислений функции соответственно, но являются весьма точными.

Высокая точность, вместе с достаточной простотой реализации делает метод Рунге-Кутты четвертого порядка одним из весьма распространенных численных методов решения задачи Коши ОДУ и систем ОДУ первого порядка.

Метод Адамса

Если используются значения в k предыдущих узлах, то говорят о k-шаговом методе интегрирования уравнения. Одним из способов построения многошаговых методов заключается в следующем. По значениям функции, вычисленным в k предшествующих узлах, строится интерполяционный полином степени (k-1) - , который используется при интегрировании дифференциального уравнения по выражению (6.3). Интеграл при этом выражается через квадратурную формулу:

где λ_l – квадратурные коэффициенты.

Полученное таким образом семейство формул называется явной k-шаговой схемой Адамса (методы Адамса-Башфорта).

Если для построения интерполяционного полинома использовать k узлов, начиная с x_i₊₁, то можно получить формулы интегрирования ОДУ, известные как неявные схемы Адамса (или методы Адамса-Моултона). Неявными эти формулы называются потому, что значение искомой функции в (i+1)-м узле - y_i₊₁ - оказывается одновременно и в левой и правой частях равенства.

Видно, что это выражение является уравнением относительно y_i₊₁, так как y_i₊₁встречается и в левой и правой его части. Однако обычно это уравнение не решается, а значение в правой части заменяется на рассчитанное по какой-либо явной формуле - например, формуле Адамса-Башфорта.

Достоинством многошаговых методов Адамса при решении ОДУ заключается в том, что в каждом узле рассчитывается только одно значение правой части ОДУ - функции F(x,y). К недостаткам можно отнести невозможность старта многошагового метода из единственной начальной точки, так как для вычислений по k-шаговой формуле необходимо знание значения функции в k узлах. Поэтому приходится (k-1) решение в первых узлах x₁, x₂, …, x_k-1получать с помощью какого-либо одношагового метода.

Другой проблемой является невозможность изменения шага в процессе решения, что легко реализуется в одношаговых методах.

Дата добавления: 2018-11-24; просмотров: 3420; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!