Интерполяция с кратными узлами.

Стр 1 из 7Следующая ⇒

Лаба 14)Трансцендентные уравнения: корни простые и кратные, локализация корня. трансцендентные уравнение- уравнение у которого нет аналитического решения. некое значение, которое обращает функция в ноль, называется корнем уравнения. способы его нахождения называются решением уравнения. если указанные корни повторяются n раз, то они называются кратными. при этом если F(x) не делиться на (x-xn)2, то корень считается простым. нахождение корня уравнения – это нахождения отрезка [а,б], в котором лежит только один корень данного уравнения. такой отрезок называется изоляцией или локацией корня.

Методы решения трансцендентных уравнений: метод бисекций

метод бисекции или метод деления отрезка пополам – простейший численный метод для решения нелинейных уравнений вида f(x)=0. предполагается только непрерывность функции. поиск основывается на теореме о промежуточных значениях.

Метод простой итерации.

исходное уравнение преобразуем к эквивалентному уравнению: x=(x). пусть известно начальное приближение (полученное на этапе отделения корней): x=x₀. подставим его в правую часть и получим новое приближение. повторяя эту процедуру, будем иметь в общем виде на некотором к-м шаге: xk=(xk-1). в качестве условия окончания вычислительного процесса можно взять выполнение неравенства:

|xk- xk-1|<ε. значение xk, удовлетворяющее ему, и есть корень уравнения.

7) метод ньютона.
метод ньютона или метод касательных часто используемый метод. он быстро сходиться (имеет квадратичную сходимость) и допускает различные модификации, приспособленные для решения векторных задач и сеточных уравнений. однако этот метод эффективен при весьма жестких ограничениях на характер функции f(x)
1- существование второй производной функции f(x) на множестве G={a≤x≤b}
2- удовлетворение первой производной условию f(x)≠0 для всех x€G

3- знакопостоянство f’(x), f’’(x) для всех x€G

поэтому его желательно использовать совместно с другими методами, например методом половинного деления, чтобы достигнуть диапазон а≤x≤b , где указанные условия начинают выполняться.

Метод секущих

метод секущих получается из метода касательных заменой f’(x^k) разностным приближением:

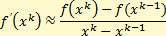
в результате получим формулу итерационного процесса:

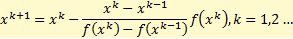
метод секущих является двухшаговым, то есть новое приближение x^k⁺¹ определяется двумя предыдущими итерациями x^k и x^k^-1 . в методе (1) необходимо задавать два начальных приближения x⁰и x¹.

скорость сходимости метода будет линейной |x^k⁺¹-x*|=O(k^k-x*).

Метод ложного положения

в основе метода лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки. Этот метод зачастую дает более быструю сходимость, чем метод деления отрезка пополам.

Обусловленность задачи нахождения корня.

под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым изменениям входных данных. задачу называют хорошо обусловленной если при малых изменениях входных данных результат также изменяется незначительно. задача называется плохо обусловленной, если малые изменения входных данных могут привести к большим изменениям решения.

Лаба 2

Приближение функций.

замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). Из заранее фиксированного (приближающего множества).

12. Интерполяция функций. – способ построения приближенных функций при котором в узлах значения приближенной и приближаемой функции совпадают.

Полиномиальная интерполяция.

многочленная интерполяция. Если есть n+1 точек, то можно построить полином степени не выше n, проходящий через эти точки. Допустим, есть точки данных. Тогда можно соорудить интерполяционный полином степени не выше 2, и легко подобрать параболу, проходящую через эти 3 точки.

Если узлов много, то такой вариант интерполяции таит в себе опасность, используется кусочно-полиномиальная интерполяция

Многочлен Лагранжа.

многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀, y₀), (x₁,y₁),…, (x_n, y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j) = y_j. В простейшем случае (n=1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Интерполяция с кратными узлами.

задача о построении многочлена минимальной степени, принимающего в некоторых точках (узлах интерполяции) заданные значения, а также заданные значения производных до некоторого порядка.

Показывается, что существует единственный многочлен 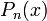степени 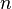, удовлетворяющий условиям:

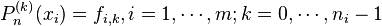, где .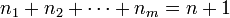

Этот многочлен называют многочленом с кратными узлами, или многочленом Эрмита.

Многочлен Эрмита.

определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике.

Дата добавления: 2018-11-24; просмотров: 287; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!