Интерполяционный многочлен Ньютона с конечными разностями вперед и назад.
Рассмотрим случай равноотстоящих узлов интерполяции, т. е.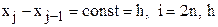 
– называется шагом.
Введем понятие конечных разностей. Пусть известны значения функции в узлах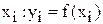 
. Составим разности значений функции:
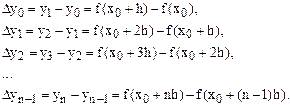
Эти разности называются разностями первого порядка.
Можно составить разности второго порядка:
.
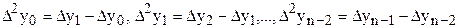Аналогично составляются разности k-го порядка:
.
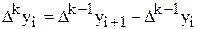18. Многочлен Чебышева.
две последовательности ортогональных многочленов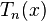 
и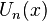 
, 
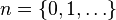Многочлен Чебышёва первого рода 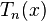характеризуется как многочлен степени 
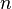со старшим коэффициентом 
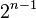, который меньше всего отклоняется от нуля на отрезке 
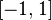. Впервые рассмотрены самим Чебышёвым.
Многочлен Чебышёва второго рода 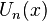характеризуется как многочлен степени 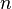со старшим коэффициентом 
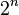, интеграл, от абсолютной величины которого по отрезку 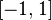принимает наименьшее возможное значение. Впервые рассмотрены в совместной работе двух учеников Чебышёва — Коркина и Золотарёва.
Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в интерполяции алгебраическими многочленами.
Погрешность интерполяции. Пути уменьшения погрешности интерполирования.
Погрешность интерполяции возникает в результате замены аппроксимирующих прямых или криволинейных отрезков ступенчатой линией и неточной работой различных устройств интерполяторов
Лаба 3
|
|
|
Метод прогонки для разрешения матриц специального вида. Устойчивость скалярной прогонки.
Метод прогонки является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трехдиагоналъной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений
На главной диагонали матрицы этой системы стоят элементы b1, b2, …, bn, над ней – элементы с1, с2,... , сn-1 под ней – элементы а2, а3,... , ап (при этом обычно все коэффициенты bi не равны нулю). Остальные элементы матрицы равны нулю.
методом прогонки, сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δi, λi по формулам (3) при i=1,2,…,n(прямая прогонка) и затем неизвестных xi по формуле (2) при i=n-1, n-2,...,1 (обратная прогонка). Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при больших размерностях систем не должно быть строгого роста погрешностей округлений. Будем называть прогонку корректной, если знаменатели прогоночных коэффициентов (3) не обращаются в нуль, и устойчивой, если |δi|<1 при всех i €{1,2,...,n}.
|
|
|
Дата добавления: 2018-11-24; просмотров: 314; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!