Сплайн-интерполяция. Кубический и параметрический сплайны.

Сплайн – линия минимальной кривизны запасенной энергии

Интерполяция – приближение, в котором изменяется приближение внутри отрезка.

Интерполяция при помощи сплайнов называется сплайн-интерполяцией

Интерполяция кубическими сплайнами - это быстрый, эффективный и устойчивый способ интерполяции функций, который является основным конкурентом полиномиальной интерполяции.

идея - интервал интерполяции разбивается на небольшие отрезки, на каждом из которых функция задается полиномом третьей степени. Коэффициенты полинома подбираются так, что на границах интервалов обеспечивается непрерывность функции, её первой и второй производных. Также есть возможность задать граничные условия - значения первой или второй производной на границах интервала. Если значения одной из производных на границе известны, то задав их, мы получаем крайне точную интерполяционную схему. Если значения неизвестны, то можно положить вторую производную на границе равно нолю и получить достаточно хорошие результаты.

Для вычисления сплайн-функции, заданной на сетке x₁ < x₂ < … < x_n, требуется упорядоченная монотонно возрастающая последовательность x_i. Это означает, что сплайн-функция y = y(x) может быть построена только для однозначной функции.

Однако, используя параметрическое задание функции, можно построить неоднозначную, в том числе замкнутую, кривую (периодический сплайн). Для этого выбирается независимая переменная t, удовлетворяющая указанным выше требованиям, и вычисляются сплайн-приближения x(t) и y(t), а затем строится кривая, проходящая через точки (x_i, y_i), соответствующие выбранным t_i.

Лаба 4

1. Метод Крамера для решения систем линейных уравнений.

Метод Крамера - это метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (то есть в случае, когда система уравнений имеет единственное решение). Основным математическим действием при решении системы уравнения методом Крамера является вычисление определителей матриц размерностью n (где n - количество уравнений в системе.

Метод исключения Гаусса для решения систем линейных уравнений.

Это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1

Приближение методом наименьших квадратов

математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Лаба 5

Формулы численного интегрирования: прямоугольников, трапеций и парабол (Симпсона).

1.Формула прямоугольников

Теперь рассмотрим первый вид приближённого вычисления: требуется вычислить определённый интеграл: .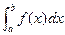

Пусть на отрезке [a,b] задана непрерывная функция y=f(x). Разделим отрезок [a,b], аналогично как в формуле трапеций: точками a=x₀ ,x_1, x₂ ,…,x_n =b на n равных частей длины Δх, где Δх=(b-a)/n.

Составим суммы: y₀ Δx+ y₁ Δx₁ + y₂ Δx₂ …+y_n _-1 Δx; Y₁ Δx+ y₂ Δx+…+y_n Δx

Каждое слагаемое этих сумм выражает площадь, полученных прямоугольников с основанием Δх, которое является шириной прямоугольника, и длиной выраженной через y_i : S_пр =a*b=y_i Δx.

Каждая из этих сумм является интегральной суммой для f(x) на отрезке [a,b], и равна площади ступенчатых фигур, а значит приближённо выражает интеграл. Вынесем Δx=(b-a)/n из каждой суммы.

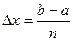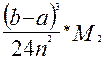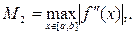Ошибка, совершаемая при вычислении интегралов по формуле прямоугольников, будет тем меньше, чем больше число n (то есть чем меньше шаг деления) . Для вычисления погрешности этого метода используется формула: P_np = , где формула средних прямоугольников: 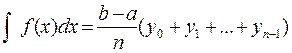(3**)

2.Формула трапеций.

Возьмём определённый интеграл∫ f(x)dx, где f(x)- непрерывная подынтегральная функция, которую мы для наглядности будем предполагать положительной. При вычислении интеграла с помощью формулы трапеций подынтегральная функция f заменяется функцией, график которой представляет собой ломанную линию. Тогда площадь криволинейной трапеции, ограниченной линиями x=a, x=b, y=0, y=f(x), а значит (следуя из геометрического смысла), и значение нужного нам интеграла, приблизительно равна сумме площадей обычных трапеций с основаниями y_i _-1 и y_i и высотой h=(b-a)/n, так как (если более привычно выражать для нас) h это Δx,aΔx=(b-a)/n при делении отрезка на n равных отрезков при помощи точек x₀ =a<x₁ <…<x_n =b. Прямые x=x_k разбивают криволинейную трапецию на n полосок. Принимая каждую из этих полосок за обыкновенную трапецию, получаем, что площадь криволинейной трапеции приблизительно равна сумме обыкновенных трапеций.

Площадь полученой полоски равна произведению полусуммы основания на высоту.

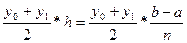
Итак, запишем сказанное выше в математическом виде:

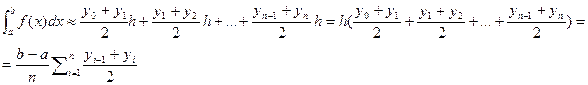
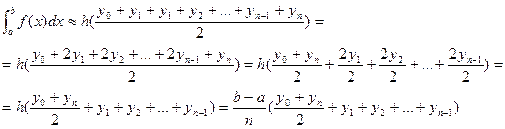(4)

Формула (4) и есть формула трапеций

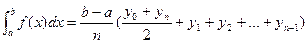Для определения погрешности интеграла вычисленного с помощью формулы трапеций используется формула: 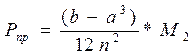где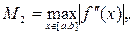

3.Формула Симпсона (формула парабол).

Существует два подхода к формуле Симпсона. В одном используется парабола в другом нет.

А) с использованием параболы.

Разделим отрезок [a;b] на чётное число равных частей n=2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x₀ ,x₁ ], [x₁ ,x₂ ] и ограниченной заданной кривой y=f(x), заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки M₀ [x₀ ,y₀ ], M₁[x₁ ,y₁ ], M₂ [x₂ ,y₂ ] и имеющей ось, параллельную оси Oy. Такую криволинейную трапецию будем называть параболической трапецией.

Уравнение параболы с осью, параллельной оси Oy, имеет вид: .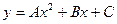

Коэффициенты A, B и C однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строятся и для других пар отрезков. Сумма параболических трапеций и даст приближённое значение интеграла. Сначала вычислим площадь одной параболической трапеции. Для этого докажем лемму.

Лемма: если криволинейная трапеция ограничена параболой 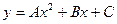, осью O_x и двумя ординатами, расстояние между которыми равно 2h, то её площадь равна: 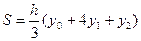(5), где y₀ и y₂ - крайние ординаты, а y₁ - ордината кривой в середине отрезка.

Доказательство:

Коэффициент в уравнение параболы 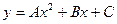определяются из следующих уравнений:

Если x₀ =-h, то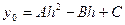

Если x₁ =0, то 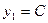(6)

Если x₂ =-h, то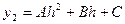

Считая коэффициенты A. B, C известными определим площадь параболической трапеции с помощью определённого интеграла:

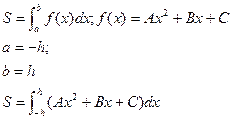
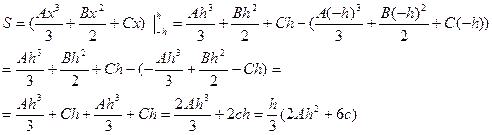
из равенства (6) следует, что

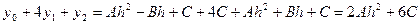
следовательно: 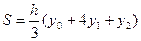пользуясь формулой (5), можно написать приближённые равенства, учитывая, что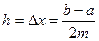

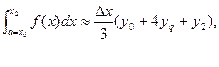
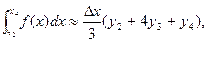
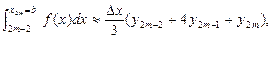
складывая левые и правые части, получим слева искомый интеграл, справа его приближённое значение:

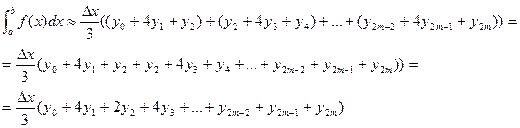
или

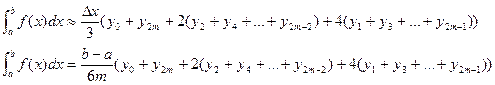
(7)

Это и есть формула Симпсона. Здесь число точек деления произвольно, но чем это число больше, тем точнее сумма в правой части равенства (6) даёт значение интеграла. Формула Симпсона даёт самое точное значение интеграла (из классических формул приближённого интегрирования), погрешность для этого метода находится по формул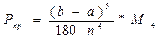е: где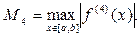

Дата добавления: 2018-11-24; просмотров: 840; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!