Априорная и апостериорная погрешность методов численного интегрирования.
численное интегрирование. Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином).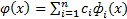 
Таким образом
где 
— априорная погрешность метода на интервале интегрирования, а 
— априорная погрешность метода на отдельном шаге интегрирования.
Метод Рунге для оценки погрешности численного интегрирования. Экстраполяция Ричардсона.
Пусть w – точное значение, к которому должен прийти численный метод (мы его не знаем). Результат численного расчета дает нам величину wh такую, что 
(2).
Теперь вычислим ту же величину w с шагом kh, где константа k может быть как больше, так и меньше единицы. Коэффициент A будет одинаковый, так как вычисление осуществляется одним и тем же методом. Получаем 
(3).
Приравняем правые части выражений (2) и (3) и пренебрежем бесконечно малыми величинами одинакового порядка малости:
.
Отсюда, учитывая (1), получим
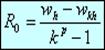(4).
Эта формула, выражающая апостериорную оценку главного члена погрешности величины w путем двойного просчета с разным шагом, носит название первой формулы Рунге. При уменьшении шага главный член погрешности будет стремиться к полной погрешности R
Вторая формула Рунге.
Так как модуль и знак апостериорной погрешности из формулы (4) известны, можно уточнить искомое значение 
. Это вторая формула Рунге. Однако теперь погрешность w corr не определена, известно лишь, что она по модулю меньше R0.
|
|
|
лаба 6
25. Численные методы решения систем обыкновенных дифференциальных уравнений (ОДУ). Задача Коши. Классификация методов.
Численное решение ДУ (частное) заключается в вычислении функции y(x) и ее производных в некоторых заданных точках 
, лежащих на определенном отрезке.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при 
, а решение отыскивается при 
.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
|
|
|
Классификация численных методов для задачи Коши
Рассмотрим разбиение отрезка 
на 
интервалов точками 
, так, что 
. Такое разбиение называют сеткой, точки - узлами сетки. Если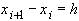 
- постоянное число (шаг сетки), не зависящее от i, то сетка называется равномерной. Численные методы позволяют находить приближенные значения для точного решения задачи Коши в узлах сетки: 
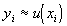. В качестве приближенного решения в таком случае выступает совокупность векторов 
(таблица), которую называют сеточной функцией.
Большинство численных методов можно записать в следующем общем виде:
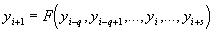
Одношаговые методы имеют вид:
- явные, 
- неявные.
Дата добавления: 2018-11-24; просмотров: 1675; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!